【数学】2019届一轮复习北师大版 简单的逻辑联结词、全称量词与存在量词学案
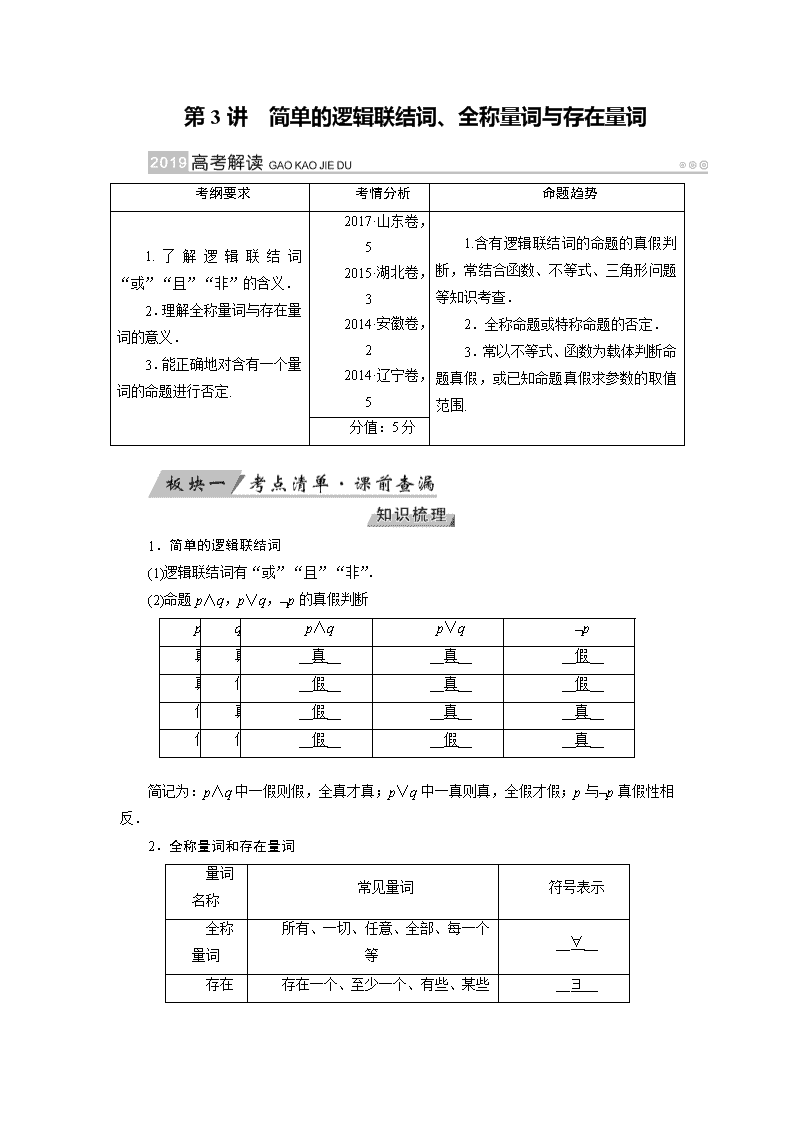
第 3 讲 简单的逻辑联结词、全称量词与存在量词
考纲要求 考情分析 命题趋势
1. 了 解 逻 辑 联 结 词
“或”“且”“非”的含义.
2.理解全称量词与存在量
词的意义.
3.能正确地对含有一个量
词的命题进行否定.
2017·山东
卷,5
2015·湖北
卷,3
2014·安徽
卷,2
2014·辽宁
卷,5
1.含有逻辑联结词的命题的真假判
断,常结合函数、不等式、三角形问题
等知识考查.
2.全称命题或特称命题的否定.
3.常以不等式、函数为载体判断命
题真假,或已知命题真假求参数的取值
范围.
分值:5 分
1.简单的逻辑联结词
(1)逻辑联结词有“或”“且”“非”.
(2)命题 p∧q,p∨q,¬p 的真假判断
p q p∧q p∨q ¬p
真 真 __真__ __真__ __假__
真 假 __假__ __真__ __假__
假 真 __假__ __真__ __真__
假 假 __假__ __假__ __真__
简记为:p∧q 中一假则假,全真才真;p∨q 中一真则真,全假才假;p 与¬p 真假性相
反.
2.全称量词和存在量词
量词
名称
常见量词 符号表示
全称
量词
所有、一切、任意、全部、每一个
等
__∀__
存在 存在一个、至少一个、有些、某些 __∃__
量词 等
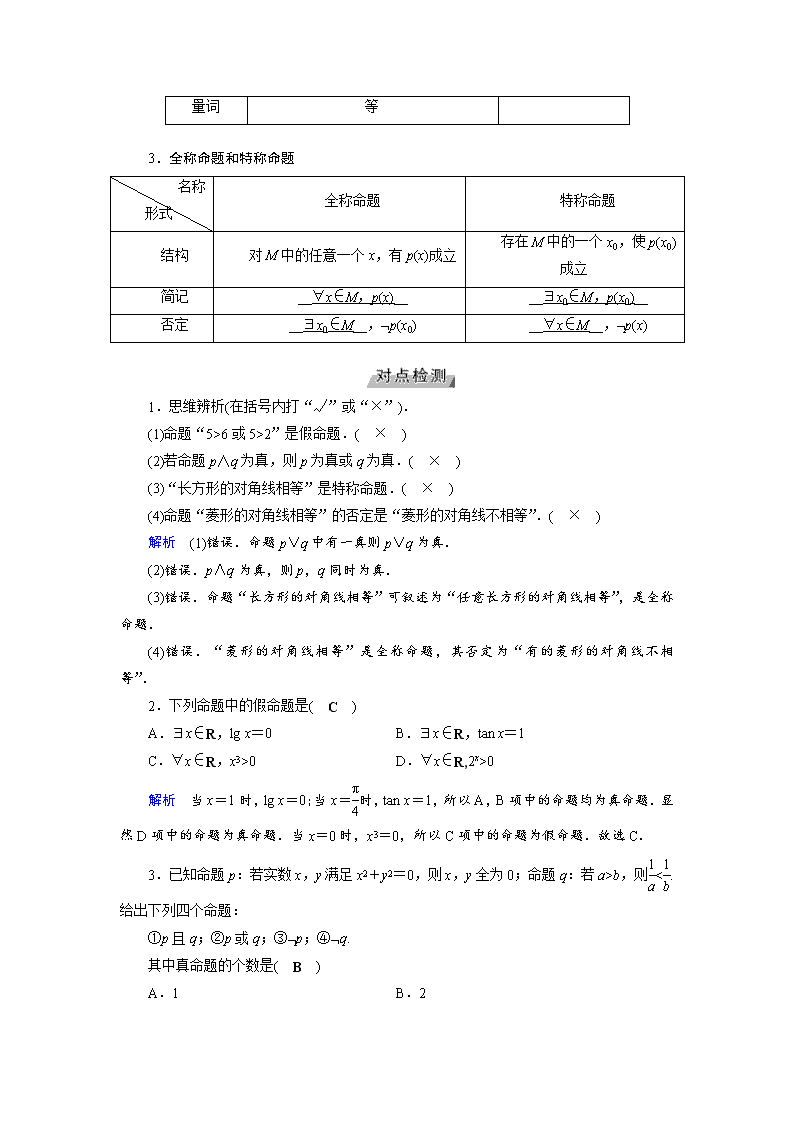
3.全称命题和特称命题
名称
形式
全称命题 特称命题
结构 对 M 中的任意一个 x,有 p(x)成立
存在 M 中的一个 x0,使 p(x0)
成立
简记 __∀x∈M,p(x)__ __∃x0∈M,p(x0)__
否定 __∃x0∈M__,¬p(x0) __∀x∈M__,¬p(x)
1.思维辨析(在括号内打“√”或“×”).
(1)命题“5>6 或 5>2”是假命题.( × )
(2)若命题 p∧q 为真,则 p 为真或 q 为真.( × )
(3)“长方形的对角线相等”是特称命题.( × )
(4)命题“菱形的对角线相等”的否定是“菱形的对角线不相等”.( × )
解析 (1)错误.命题 p∨q 中有一真则 p∨q 为真.
(2)错误.p∧q 为真,则 p,q 同时为真.
(3)错误.命题“长方形的对角线相等”可叙述为“任意长方形的对角线相等”,是全
称命题.
(4)错误.“菱形的对角线相等”是全称命题,其否定为“有的菱形的对角线不相等”.
2.下列命题中的假命题是( C )
A.∃x∈R,lg x=0 B.∃x∈R,tan x=1
C.∀x∈R,x3>0 D.∀x∈R,2x>0
解析 当 x=1 时,lg x=0;当 x=π
4
时,tan x=1,所以 A,B 项中的命题均为真命题.显
然 D 项中的命题为真命题.当 x=0 时,x3=0,所以 C 项中的命题为假命题.故选 C.
3.已知命题 p:若实数 x,y 满足 x2+y2=0,则 x,y 全为 0;命题 q:若 a>b,则1
a<1
b.
给出下列四个命题:
①p 且 q;②p 或 q;③¬p;④¬q.
其中真命题的个数是( B )
A.1 B.2
C.3 D.4
解析 ∵命题 p 为真命题,q 为假命题,∴p 或 q,¬q 为真命题.故选 B.
4.已知命题 p:∃n∈N,2n>1 000,则¬p 为( A )
A.∀n∈N,2n≤1 000
B.∀n∈N,2n>1 000
C.∃n∈N,2n≤1 000
D.∃n∈N,2n<1 000
解析 由于特称命题的否定是全称命题,因而¬p:∀n∈N,2n≤1 000.故选 A.
5.在一次跳伞训练中,甲、乙两位学员各跳一次,设命题 p 是“甲降落在指定范围”,
q 是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为
( A )
A.(¬p)∨(¬q) B.p∨(¬q)
C.(¬p)∧(¬q) D.p∨q
解析 因为 p 是“甲降落在指定范围”,q 是“乙降落在指定范围”,则¬p 是“甲没
有降落在指定范围”, ¬q 是“乙没有降落在指定范围”,所以命题“至少有一位学员没有
降落在指定范围”可表示为(¬p)∨(¬q).故选 A.
一 含有逻辑联结词的命题的真假判断
(1)判断含有逻辑联结词的命题真假的步骤:
①先判断简单命题 p,q 的真假;
②再根据真值表判断含有逻辑联结词命题的真假.
(2)含逻辑联结词命题真假的等价关系:
①p∨q 真⇔p,q 至少有一个真⇔(¬p)∧(¬q)假;
②p∨q 假⇔p,q 均假⇔(¬p)∧(¬q)真;
③p∧q 真⇔p,q 均真⇔(¬p)∨(¬q)假;
④p∧q 假⇔p,q 至少有一个假⇔(¬p)∨(¬q)真;
⑤¬p 真⇔p 假;¬p 假⇔p 真.
【例 1】 (1)(2017·山东卷)已知命题 p:∃x∈R,x2-x+1≥0;命题 q:若 a2
0 恒成立,∴p 为真命题.对于命题 q,取 a=2,b=-
3,22<(-3)2,而 2>-3,∴q 为假命题,¬q 为真命题.因此 p∧(¬q)为真命题.故选 B.
(2)∵y=2x 在 R 上为增函数,
y=-2-x=-
1
2 x 在 R 上为增函数,
∴y=2x-2-x 在 R 上为增函数,故 p1 是真命题.
y=2x+2-x 在 R 上为减函数是错误的,故 p2 是假命题.
∴q1:p1∨p2 是真命题,因此排除 B 项和 D 项,q2:p1∧p2 是假命题,q3:(¬p1)∨p2 是
假命题,排除 A 项.故选 C.
二 全称命题与特称命题
(1)全称命题与特称命题真假的判断方法:
命题
名称
真
假
判断方法一
判断方
法二
全称
命题
真 所有对象使命题真
否定为
假
假 存在一个对象使命题假
否定为
真
特称
命题
真 存在一个对象使命题真
否定为
假
假 所有对象使命题假
否定为
真
(2)全称命题与特称命题的否定要注意以下两点:
①否定量词:确定命题所含量词的类型,省去量词的要结合命题的含义加上量词,再对
量词进行否定;
②否定结论:对原命题的结论进行否定.
【例 2】 (1)设命题 p:∃n∈N,n2>2n,则¬p 为( C )
A.∀n∈N,n2>2n B.∃n∈N,n2≤2n
C.∀n∈N,n2≤2n D.∃n∈N,n2=2n
(2)命题“对任意 x∈R,都有 x2≥ln 2”的否定为( D )
A.对任意 x∈R,都有 x22n”的否定是“∀n∈N,n2≤2n”.
(2)按照“任意”改“存在”,结论变否定的模式,命题的否定为“存在 x0∈R,使得
x200
B.∀x∈N*,(x-1)2>0
C.∃x0∈R,ln x0<1
D.∃x0∈R,tan x0=2
(2)已知命题 p:∀x>0,x+4
x
≥4;命题 q:∃x0∈(0,+∞),2x0=1
2
,则下列判断正确
的是( C )
A.p 是假命题 B.q 是真命题
C.p∧(¬q)是真命题 D.(¬p)∧q 是真命题
解析 (1)因为 2x-1>0,对∀x∈R 恒成立,所以 A 项中的命题是真命题;当 x=1 时,(x
-1)2=0,所以 B 项中的命题是假命题;存在 00 时,x+4
x
≥2 x·4
x
=4,p 是真命题;当 x>0 时,2x>1,q 是假命题,所以 p
∧(¬q)是真命题,(¬p)∧q 是假命题.
三 根据命题的真假求参数的取值范围
根据命题的真假求参数取值范围的求解策略
(1)含有逻辑联结词的命题要先确定构成命题的(一个或两个)简单命题的真假,求出此时
命题成立的参数的取值范围,再求出含逻辑联结词的命题成立的参数的取值范围.
(2)全称命题可转化为恒成立问题.
【例 4】 已知命题 p:函数 y=x2-2x+a 在区间(1,2)上有 1 个零点,命题 q:函数 y=
x2+(2a-3)x+1 的图象与 x 轴交于不同的两点,如果 p∧q 是假命题,p∨q 是真命题,求 a
的取值范围.
解析 若命题 p 为真命题,则函数 y=x2-2x+a 在区间(1,2)上有 1 个零点.
因为二次函数图象开口向上,对称轴为 x=1,
所以 12-2×1+a<0,
22-2×2+a>0,
所以 00,得 4a2-12a+5>0,解得 a<1
2
或 a>5
2.
因为 p∧q 是假命题,p∨q 是真命题,所以 p,q 一真一假.
①若 p 真 q 假,则
05
2
, 所以 a≤0 或 a>5
2.
故实数 a 的取值范围是(-∞,0]∪
1
2
,1 ∪
5
2
,+∞
.
1.已知命题 p:复数 z=1+i
i
在复平面内所对应的点位于第四象限;命题 q:∃x0>0,2
-x0=ex0,则下列命题中为真命题的是( A )
A.p∧q B.(¬p)∧q
C.p∧(¬q) D.(¬p)∧(¬q)
解析 化简 z=1+i
i
=1+i·i
i·i
=1-i,故命题 p 是真命题;在同一坐标系中同时画出函
数 f(x)=2-x 和函数 g(x)=ex 的图象(图略),观察发现图象的交点在第一象限,故命题 q 是
真命题.再根据复合命题的真值表,知 A 项是正确的.
2.命题 p:对任意的 x∈R,f(x)=2cos2x+ 3sin 2x≤3,则( D )
A.p 是假命题;¬p:存在 x0∈R,使得 f(x0)=2cos2x0+ 3sin 2x0≤3
B.p 是假命题;¬p:存在 x0∈R,使得 f(x0)=2cos2x0+ 3sin 2x0>3
C.p 是真命题;¬p:存在 x0∈R,使得 f(x0)=2cos2x0+ 3sin 2x0≤3
D.p 是真命题;¬p:存在 x0∈R,使得 f(x0)=2cos2x0+ 3sin 2x0>3
解析 根据全称命题的否定是特称命题,可知全称命题 p 的否定是存在 x0∈R,使得 f(x0)
=2cos2x0+ 3sin 2x0>3.另外,f(x)=2cos2x+ 3sin 2x= 3sin 2x+cos 2x+1=2sin 2x+π
6 +
1≤3.故选 D.
3.若命题“∃x0∈R,x20-2x0+m≤0”是假命题,则实数 m 的取值范围是__(1,+∞)__.
解析 由题意,知命题“∀x∈R,x2-2x+m>0”是真命题,故Δ=(-2)2-4m<0,即
m>1.
4.已知命题 p:关于 x 的方程 x2-mx-2=0 在 x∈[0,1]时有解;命题 q:f(x)=
log2
x2-2mx+1
2 在 x∈[1,+∞)时单调递增.若綈 p 为真命题,p∨q 是真命题,则实数 m
的取值范围为__
-1,3
4 __.
解析 根据题意,关于 x 的方程 x2-mx-2=0 在 x∈[0,1]时有解,可得 1-m-2≥0,
从 而 求 得 m≤ - 1 ; f(x) = log2
x2-2mx+1
2 在 x ∈ [1 , + ∞) 时 单 调 递 增 , 可 得
m≤1,
1-2m+1
2>0, 解得 m<3
4.根据綈 p 为真命题,p∨q 是真命题,可知 p 假 q 真,所以实数
m 的取值范围为 -1,3
4 .
易错点 混淆否命题与命题的否定
错因分析:否命题既要否定条件,又要否定结论,而命题的否定只否定结论.
【例 1】 写出命题“若 a2+b2=0,则实数 a,b 全为零”的否定及否命题.
解析 命题的否定:若 a2+b2=0,则实数 a,b 不全为零.
命题的否命题:若 a2+b2≠0,则实数 a,b 不全为零.
【跟踪训练 1】 (2016·浙江卷)命题“∀x∈R,∃n∈N*,使得 n≥x2”的否定形式是
( D )
A.∀x∈R,∃n∈N*,使得 n0,总有 ex≥1,则¬p 为( B )
A.存在 x0≤0,使得 ex0<1 B.存在 x0>0,使得 ex0<1
C.对任意 x>0,总有 ex<1 D.对任意 x≤0,总有 ex<1
解析 因为全称命题的否定是特称命题,所以,命题 p:对任意 x>0,总有 ex≥1 的否
定¬p:存在 x0>0,使得 ex0<1.故选 B.
2.已知命题 p:∃x0∈R,tan x0=1;命题 q:∀x∈R,x2>0.下列结论正确的是
( D )
A.命题 p∧q 是真命题 B.命题 p∧(¬q)是假命题
C.命题(¬p)∨q 是真命题 D.命题(¬p)∧(¬q)是假命题
解析 取 x0=π
4
,有 tanπ
4
=1,故命题 p 是真命题;当 x=0 时,x2=0,故命题 q 是假命
题.再根据复合命题的真值表,知 D 项是正确的.
3.已知函数 f(x)=x2-2ax+2a2-2(a≠0),g(x)=-ex-1
ex
,则下列命题为真命题的是
( B )
A.∀x∈R,都有 f(x)<g(x)
B.∀x∈R,都有 f(x)>g(x)
C.∃x0∈R,使得 f(x0)<g(x0)
D.∃x0∈R,使得 f(x0)=g(x0)
解析 函数 f(x)=x2-2ax+2a2-2=(x-a)2+a2-2≥a2-2>-2,g(x)=-ex-1
ex
=-
ex+1
ex ≤-2,显然∀x∈R,都有 f(x)>g(x).故选 B.
4.命题“存在 x∈R,使 x2+ax-4a<0 为假命题”是命题“-16≤a≤0”的( A )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
解析 依题意,知 x2+ax-4a≥0 恒成立,则Δ=a2+16a≤0,解得-16≤a≤0.故选 A.
5.命题 p:x∈R,ax2+ax+1≥0,若¬p 是真命题,则实数 a 的取值范围是( D )
A.(0,4] B.[0,4]
C.(-∞,0)∪[4,+∞) D.(-∞,0)∪(4,+∞)
解析 命题 p 的否定是¬p:∃x∈R,ax2+ax+1<0 成立,即不等式 ax2+ax+1<0 有解.
当 a=0 时,1<0,不等式无解;
当 a≠0 时,要使不等式有解,须 a2-4a>0,
解得 a>4 或 a<0,
综上,a 的取值范围是(-∞,0)∪(4,+∞).故选 D.
6.已知命题 p1:∀x∈(0,+∞),有 3x>2x,p2:∃θ∈R,sin θ+cos θ=3
2
,则在命题
q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2 和 q4:p1∧(¬p2)中,真命题是( C )
A.q1,q3 B.q2,q3
C.q1,q4 D.q2,q4
解析 因为 y=
3
2 x 在 R 上是增函数,即 y=
3
2 x>1 在(0,+∞)上恒成立,所以 p1 是真
命题;sin θ+cos θ= 2sin θ+π
4 ≤ 2,所以命题 p2 是假命题,¬p2 是真命题,所以命题 q1:
p1∨p2,q4:p1∧(¬p2)是真命题.故选 C.
二、填空题
7.已知函数 f(x)的定义域为(a,b),若“∃x0∈(a,b),f(x0)+f(-x0)≠0”是假命题,
则 f(a+b)=__0__.
解析 若“∃x0∈(a,b),f(x0)+f(-x0)≠0”是假命题,则“∀x∈(a,b),f(x)+f(-x)
=0”是真命题,即 f(-x)=-f(x),则函数 f(x)是奇函数,则 a+b=0,即 f(a+b)=0.
8.命题“∃x∈R,2x2-3ax+9<0”为假命题,则实数 a 的取值范围是__[-2 2,2 2]__.
解析 由题可知“∀x∈R,2x2 -3ax+9≥0”为真命题,所以可得Δ=(-3a)2 -
4×2×9≤0,解得-2 2≤a≤2 2.
9.给出下列命题:①函数 y=sin
3
2π+x 是偶函数;②函数 y=cos 2x+π
4 图象的一条
对称轴方程为 x=π
8
;③对于任意实数 x,有 f(-x)=-f(x),g(-x)=g(x),且 x>0 时,f′(x)
>0,g′(x)>0,则 x<0 时,f′(x)>g′(x);④若∀x∈R,函数 f(x)满足 f(x+2)=-f(x),
则 4 是该函数的一个周期;其中真命题为__①③④__(写出所有真命题的序号).
解析 对于①,y=sin
3
2π+x =-cos x 是偶函数,正确;对于②,把 x=π
8
代入 2x+π
4
,
有 2×π
8
+π
4
=π
2
,而 cosπ
2
=0,故 x=π
8
不是函数图象的一条对称轴方程,错误;对于③,根据
函数的奇偶性和导数与函数单调性的关系,可以得出,当 x<0 时,有 f′(x)>0,而 g′(x)<0,
故 x<0 时,f′(x)>g′(x),正确;对于④,令 x=x+2,可以得到 f(x+4)=-f(x+2)=f(x),
根据周期的定义,可知 4 是该函数的一个周期,正确.
三、解答题
10.(2018·湖南岳阳一中月考)已知命题 p:(x+1)(x-5)≤0,命题 q:1-m≤x≤1+m(m>0).
(1)若 p 是 q 的充分条件,求实数 m 的取值范围;
(2)若 m=5,p∨q 为真命题,p∧q 为假命题,求实数 x 的取值范围.
解析 (1)设使命题 p 成立的集合为 A,命题 q 成立的集合为 B,则
A={x|-1≤x≤5},B={x|1-m≤x≤1+m},所以 A⊆B,
所以
m>0,
1+m≥5,
1-m≤-1,
解得 m≥4.故实数 m 的取值范围为[4,+∞).
(2)根据条件可知 p,q 一真一假.
当 p 真 q 假时,
-1≤x≤5,
x>6 或 x<-4,
无解.
当 p 假 q 真时, x>5 或 x<-1,
-4≤x≤6,
解得-4≤x<-1 或 52,
a≤1,
则 a<-1,
故实数 a 的取值范围是(-∞,-1).
12.已知 a∈R,命题 p:∀x∈[1,2],x2-a≥0,命题 q:∃x∈R,x2+2ax+2-a=0.
(1)若命题 p 为真命题,求实数 a 的取值范围;
(2)若命题 p∨q 为真命题,命题 p∧q 为假命题,求实数 a 的取值范围.
解析 (1)因为命题 p:∀x∈[1,2],x2-a≥0,令 f(x)=x2-a,根据题意,只要 x∈[1,2]
时,f(x)min≥0 即可,也就是 1-a≥0⇒a≤1,即 a 的取值范围是(-∞,1].
(2)由(1)可知,命题 p 为真时,a≤1,
命题 q 为真时,Δ=4a2-4(2-a)≥0,解得 a≤-2 或 a≥1.
因为命题 p∨q 为真命题,命题 p∧q 为假命题,所以命题 p 与命题 q 一真一假,
当命题 p 为真、命题 q 为假时, a≤1,
-2<a<1
⇒-2<a<1;
当命题 p 为假、命题 q 为真时, a>1,
a≤-2 或 a≥1
⇒a>1.
综上,实数 a 的取值范围是(-2,1)∪(1,+∞).