【数学】2020届一轮复习苏教版函数y=Asin(ωx＋φ)的图象及应用学案

【数学】2020届一轮复习苏教版函数y=Asin(ωx＋φ)的图象及应用学案

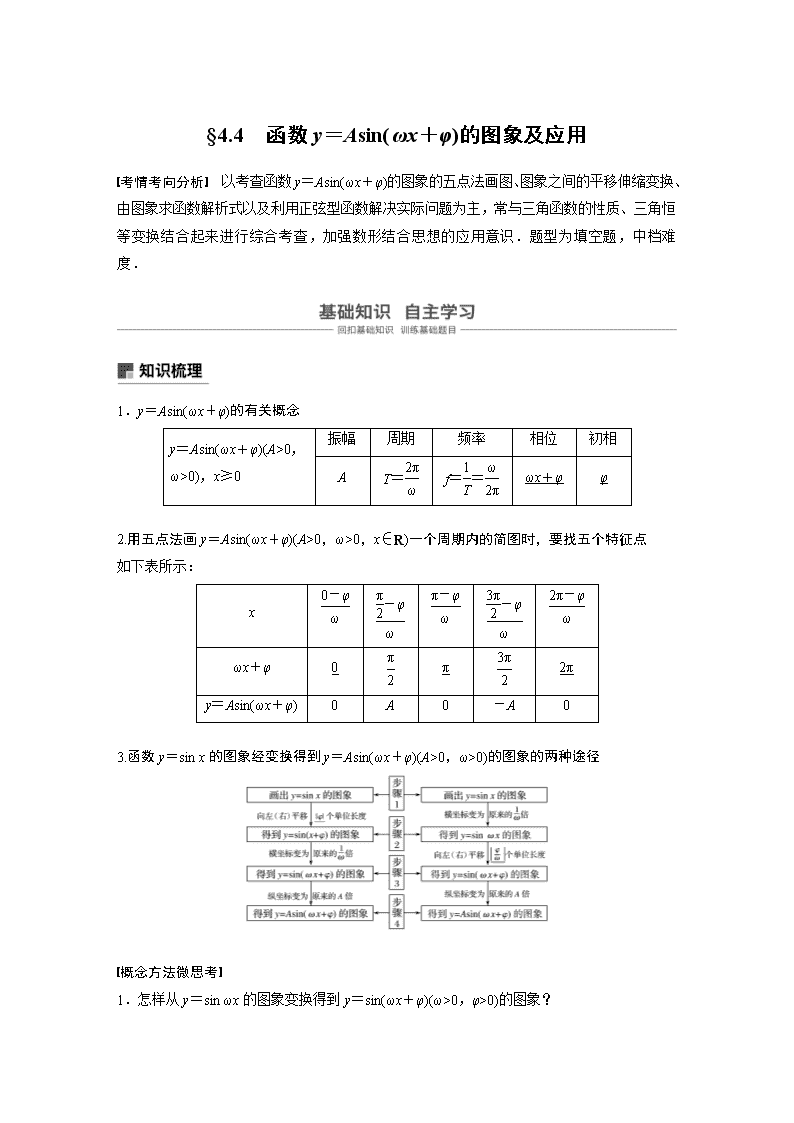
§4.4　函数 y＝Asin(ωx＋φ)的图象及应用 考情考向分析 　以考查函数 y＝Asin(ωx＋φ)的图象的五点法画图、图象之间的平移伸缩变换、 由图象求函数解析式以及利用正弦型函数解决实际问题为主，常与三角函数的性质、三角恒 等变换结合起来进行综合考查，加强数形结合思想的应用意识．题型为填空题，中档难 度． 1．y＝Asin(ωx＋φ)的有关概念 振幅 周期 频率 相位 初相y＝Asin(ωx＋φ)(A>0， ω>0)，x≥0 A T＝2π ω f＝1 T＝ω 2π ωx＋φ φ 2.用五点法画 y＝Asin(ωx＋φ)(A>0，ω>0，x∈R)一个周期内的简图时，要找五个特征点 如下表所示： x 0－φ ω π 2－φ ω π－φ ω 3π 2 －φ ω 2π－φ ω ωx＋φ 0 π 2 π 3π 2 2π y＝Asin(ωx＋φ) 0 A 0 －A 0 3.函数 y＝sin x 的图象经变换得到 y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种途径 概念方法微思考 1．怎样从 y＝sin ωx 的图象变换得到 y＝sin(ωx＋φ)(ω>0，φ>0)的图象？ 提示　向左平移φ ω个单位长度． 2．函数 y＝sin(ωx＋φ)图象的对称轴是什么？ 提示　x＝kπ ω＋ π 2ω－φ ω(k∈Z)． 题组一　思考辨析 1．判断下列结论是否正确(请在括号中打“√”或“×”) (1)y＝sin (x－π 4 )的图象是由 y＝sin (x＋π 4 )的图象向右平移π 2个单位长度得到的．(　√　) (2)将函数 y＝sin ωx 的图象向右平移 φ(φ>0)个单位长度，得到函数 y＝sin(ωx－φ)的图 象．(　×　) (3)函数 y＝Acos(ωx＋φ)的最小正周期为 T，那么函数图象的两个相邻对称中心之间的距离为 T 2.(　√　) (4)函数 y＝sin x 的图象上各点纵坐标不变，横坐标缩短为原来的1 2，所得图象对应的函数解析 式为 y＝sin 1 2x.(　×　) 题组二　教材改编 2．[P39T2]为了得到函数 y＝2sin(2x－π 3)的图象，可以将函数 y＝2sin 2x 的图象向________平 移________个单位长度． 答案　右　π 6 3．[P40T5]y＝2sin (1 2x－π 3)的振幅、频率和初相分别为__________________． 答案　2，1 4π，－π 3 4．[P41T1]如图，某地一天从 6～14 时的温度变化曲线近似满足函数 y＝Asin(ωx＋φ)＋b，则 这段曲线的函数解析式为__________________________． 答案　y＝10sin(π 8x＋3π 4 )＋20，x∈[6,14] 解析　从题图中可以看出，从 6～14 时的是函数 y＝Asin(ωx＋φ)＋b 的半个周期， 所以 A＝1 2×(30－10)＝10， b＝1 2×(30＋10)＝20， 又1 2×2π ω＝14－6，所以 ω＝π 8. 又π 8×10＋φ＝2π＋2kπ，k∈Z，取 φ＝3π 4 ， 所以 y＝10sin(π 8x＋3π 4 )＋20，x∈[6,14]． 题组三　易错自纠 5 ． 将 函 数 y ＝ 2sin (2x＋π 6)的 图 象 向 右 平 移 1 4个 周 期 后 ， 所 得 图 象 对 应 的 函 数 为 ________________． 答案　y＝2sin(2x－π 3) 解析　函数 y＝2sin (2x＋π 6)的周期为 π，将函数 y＝2sin (2x＋π 6)的图象向右平移1 4个周期，即π 4 个单位长度， 所得函数为 y＝2sin[2(x－π 4 )＋π 6]＝2sin(2x－π 3). 6．y＝cos(x＋1)图象上相邻的最高点和最低点之间的距离是________． 答案　 π2＋4 解析　相邻最高点与最低点的纵坐标之差为 2，横坐标之差恰为半个周期 π，故它们之间的 距离为 π2＋4. 7.若函数 f(x)＝Asin(ωx＋φ)(A>0，ω>0，0<φ<π)的部分图象如图所示，则 f (π 4 )的值为 ________． 答案　 3 解析　由题干图象可知 A＝2，3 4T＝11π 12 －π 6＝3π 4 ， ∴T＝π，∴ω＝2，∵当 x＝π 6时，函数 f(x)取得最大值， ∴2×π 6＋φ＝π 2＋2kπ(k∈Z)，∴φ＝π 6＋2kπ(k∈Z)， 又 0<φ<π，∴φ＝π 6，∴f(x)＝2sin(2x＋π 6)， 则 f (π 4 )＝2sin(π 2＋π 6 )＝2cos π 6＝ 3. 题型一　函数 y＝Asin(ωx＋φ)的图象及变换 例 1 已知函数 f(x)＝Asin(ωx＋φ)(A > 0，ω > 0，－π 2 < φ < π 2) 的最小正周期是 π，且当 x＝π 6时，f(x)取得最大值 2. (1)求 f(x)的解析式； (2)作出 f(x)在[0，π]上的图象(要列表)． 解　(1)因为函数 f(x)的最小正周期是 π，所以 ω＝2. 又因为当 x＝π 6时，f(x)取得最大值 2. 所以 A＝2， 同时 2×π 6＋φ＝2kπ＋π 2，k∈Z， φ＝2kπ＋π 6，k∈Z， 因为－π 2<φ<π 2，所以 φ＝π 6， 所以 f(x)＝2sin(2x＋π 6). (2)因为 x∈[0，π]，所以 2x＋π 6∈[π 6，13π 6 ]， 列表如下： 2x＋π 6 π 6 π 2 π 3π 2 2π 13π 6 x 0 π 6 5π 12 2π 3 11π 12 π f(x) 1 2 0 －2 0 1 描点、连线得图象： 引申探究 在本例条件下，若将函数 f(x)的图象向右平移 m(m>0)个单位长度后得到函数 y＝g(x)的图象， 且 y＝g(x)是偶函数，求 m 的最小值． 解　由已知得 y＝g(x)＝f(x－m)＝2sin[2(x－m)＋π 6]＝2sin [2x－(2m－π 6)]是偶函数， 所以 2m－π 6＝π 2(2k＋1)，k∈Z，m＝kπ 2 ＋π 3，k∈Z， 又因为 m>0，所以 m 的最小值为π 3. 思维升华 (1)y＝Asin(ωx＋φ)的图象可用“五点法”作简图得到，可通过变量代换 z＝ωx＋φ 计算五点坐标． (2)由函数 y＝sin x 的图象通过变换得到 y＝Asin(ωx＋φ)的图象有两条途径：“先平移后伸缩” 与“先伸缩后平移”． 跟踪训练 1　(1)(2018·南通、泰州模拟)在平面直角坐标系 xOy 中，将函数 y＝sin (2x＋π 3)的图 象向右平移 φ (0 < φ < π 2)个单位长度，若平移后得到的图象经过坐标原点，则 φ 的值为 ________． 答案　π 6 解析　y＝sin (2x＋π 3)的图象向右平移 φ 个单位长度后得到 y＝sin(2x－2φ＋π 3)， 又 sin(－2φ＋π 3)＝0，∴－2φ＋π 3＝kπ(k∈Z)， 又 0<φ<π 2，∴φ＝π 6. (2)已知函数 f(x)＝sin(ωx＋π 6)(0<ω<2)满足条件：f (－1 2 )＝0，为了得到函数 y＝f(x)的图象， 可将函数 g(x)＝cos ωx 的图象向右平移 m(m>0)个单位长度，则 m 的最小值为________． 答案　1 解析　由题意得 sin(－1 2ω＋π 6)＝0，即－1 2ω＋π 6＝kπ(k∈Z)，则 ω＝π 3－2kπ(k∈Z)， 结合 0<ω<2，得 ω＝π 3，所以 f(x)＝sin(π 3x＋π 6)＝cos(π 2－π 3x－π 6)＝cos[π 3 (x－1)]， 所以只需将函数 g(x)＝cos π 3x 的图象向右至少平移 1 个单位长度， 即可得到函数 y＝f(x)的图象． 题型二　由图象确定 y＝Asin(ωx＋φ)的解析式 例 2 (1)已知函数 f(x)＝sin(ωx＋φ)(ω > 0，|φ| < π 2)的部分图象如图所示，则 y＝f (x＋π 6 )取得最 小值时 x 的集合为________________． 答案　Error! 解析　根据题干所给图象，周期 T＝4×(7π 12－π 3)＝π，故 π＝2π ω，∴ω＝2， 因此 f(x)＝sin(2x＋φ)，另外图象经过点(7π 12，0)，代入有 2×7π 12＋φ＝π＋2kπ(k∈Z)， 再由|φ|<π 2，得 φ＝－π 6，∴f(x)＝sin(2x－π 6)， ∴f (x＋π 6 )＝sin(2x＋π 6)， 当 2x＋π 6＝－π 2＋2kπ(k∈Z)，即 x＝－π 3＋kπ(k∈Z)时，y＝f (x＋π 6 )取得最小值． (2)(2019·江苏省扬州中学月考)函数 f(x)＝6cos 2ωx 2 ＋ 3sin ωx－3(ω>0)在一个周期内的图象 如图所示，A 为图象的最高点，B，C 为图象与 x 轴的交点，且△ABC 为正三角形． ①求 ω 的值及函数 f(x)的值域； ②若 f(x0)＝8 3 5 ，且 x0∈(－10 3 ，2 3)，求 f(x0＋1)的值． 解　①由已知可得，f(x)＝3cos ωx＋ 3sin ωx＝2 3sin(ωx＋π 3)， ∴函数 f(x)的值域为[－2 3，2 3]， ∴正三角形 ABC 的高为 2 3，从而 BC＝4， ∴函数 f(x)的周期 T＝4×2＝8，即2π ω＝8，ω＝π 4. ②∵f(x0)＝8 3 5 ， 由①有 f(x0)＝2 3sin(π 4x0＋π 3)＝8 3 5 ， 即 sin(π 4x0＋π 3)＝4 5， 由 x0∈(－10 3 ，2 3)，知 π 4x0＋π 3∈(－π 2，π 2)， ∴cos(π 4x0＋π 3)＝ 1－(4 5 )2＝3 5. ∴f(x0＋1)＝2 3sin(π 4x0＋π 4＋π 3) ＝2 3sin[(π 4x0＋π 3)＋π 4] ＝2 3[sin(π 4x0＋π 3)cosπ 4＋cos(π 4x0＋π 3)sinπ 4] ＝2 3(4 5 × 2 2 ＋3 5 × 2 2 )＝7 6 5 . 思维升华 y＝Asin(ωx＋φ)中 φ 的确定方法 (1)代入法：把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或 把图象的最高点或最低点代入． (2)五点法：确定 φ 值时，往往以寻找“五点法”中的特殊点作为突破口． 跟踪训练 2 已知函数 f(x)＝Asin(ωx＋φ)＋B (A > 0，ω > 0，|φ| < π 2)的部分图象如图所示，将函 数 f(x)的图象向左平移 m(m>0)个单位长度后，得到函数 g(x)的图象关于点(π 3， 3 2 )对称，则 m 的最小值为________． 答案　 π 12 解析　依题意得Error!解得Error! T 2＝π ω＝2π 3 －π 6＝π 2， 故 ω＝2，则 f(x)＝ 3sin(2x＋φ)＋ 3 2 . 又 f (π 6 )＝ 3sin(π 3＋φ )＋ 3 2 ＝3 3 2 ， 故π 3＋φ＝π 2＋2kπ(k∈Z)，即 φ＝π 6＋2kπ(k∈Z)． 因为|φ|<π 2，故 φ＝π 6， 所以 f(x)＝ 3sin(2x＋π 6)＋ 3 2 . 将函数 f(x)的图象向左平移 m 个单位长度后，得到 g(x)＝ 3sin(2x＋π 6＋2m)＋ 3 2 的图象， 又函数 g(x)的图象关于点(π 3， 3 2 )对称，即 h(x)＝ 3sin (2x＋π 6＋2m)的图象关于点(π 3，0 )对 称， 故 3sin(2π 3 ＋π 6＋2m)＝0，即5π 6 ＋2m＝kπ(k∈Z)，故 m＝kπ 2 －5π 12(k∈Z)． 又 m>0，所以 m 的最小值为 π 12. 题型三　三角函数图象、性质的综合应用 命题点 1　图象与性质的综合问题 例 3 已知函数 f(x)＝2sin(ωx＋φ)(ω > 0，|φ| < π 2)的部分图象如图所示，若 f(0)＝ 3，且AB → ·BC → ＝π2 8 －8，B，C 分别为最高点与最低点． (1)求函数 f(x)的单调递增区间； (2)若将 f(x)的图象向左平移π 6个单位长度，得到函数 g(x)的图象，求函数 g(x)在区间[0，π 2 ]上 的最大值和最小值． 解　(1)由 f(0)＝ 3，可得 2sin φ＝ 3，即 sin φ＝ 3 2 . 又∵|φ|<π 2，∴φ＝π 3. 由题意可知，AB → ＝(1 4T，2)，BC → ＝(1 2T，－4)， 则AB → ·BC → ＝T2 8 －8＝π2 8 －8，∴T＝π. 故 ω＝2，∴f(x)＝2sin(2x＋π 3). 由－π 2＋2kπ≤2x＋π 3≤π 2＋2kπ，k∈Z， 解得－5π 12＋kπ≤x≤ π 12＋kπ，k∈Z， ∴函数 f(x)的单调递增区间为[－5π 12＋kπ， π 12＋kπ]，k∈Z. (2)由题意将 f(x)的图象向左平移π 6个单位长度，得到函数 g(x)的图象， ∴g(x)＝f (x＋π 6 )＝2sin[2(x＋π 6 )＋π 3] ＝2sin(2x＋2π 3 ). ∵x∈[0，π 2 ]， ∴2x＋2π 3 ∈[2π 3 ，5π 3 ]，sin(2x＋2π 3 )∈[－1， 3 2 ]. ∴当 2x＋2π 3 ＝2π 3 ，即 x＝0 时，sin(2x＋2π 3 )＝ 3 2 ， g(x)取得最大值 3， 当 2x＋2π 3 ＝3π 2 ，即 x＝5π 12时，sin(2x＋2π 3 )＝－1， g(x)取得最小值－2. 命题点 2　函数零点(方程根)问题 例 4 已知关于 x 的方程 2sin2x－ 3sin 2x＋m－1＝0 在(π 2，π )上有两个不同的实数根，则 m 的取值范围是____________． 答案　(－2，－1) 解析　方程 2sin2x－ 3sin 2x＋m－1＝0 可转化为 m＝1－2sin2x＋ 3sin 2x＝cos 2x＋ 3sin 2x ＝2sin(2x＋π 6)，x∈(π 2，π ). 设 2x＋π 6＝t，则 t∈(7 6π，13 6 π)， ∴题目条件可转化为m 2＝sin t，t∈(7 6π，13 6 π)有两个不同的实数根． ∴y＝m 2和 y＝sin t，t∈(7 6π，13 6 π)的图象有两个不同交点，如图： 由图象观察知，m 2的取值范围是(－1，－1 2)， 故 m 的取值范围是(－2，－1)． 引申探究 本例中，若将“有两个不同的实数根”改成“有实根”，则 m 的取值范围是__________． 答案　[－2,1) 解析　由上例题知，m 2的取值范围是[－1，1 2)， ∴－2≤m<1，∴m 的取值范围是[－2,1)． 命题点 3　三角函数模型 例 5 据市场调查，某种商品一年内每件出厂价在 7 千元的基础上，按月呈 f(x)＝Asin(ωx＋φ) ＋B (A > 0，ω > 0，|φ| < π 2)的模型波动(x 为月份)，已知 3 月份达到最高价 9 千元，9 月份价 格最低，为 5 千元，则 7 月份的出厂价格为______元． 答案　6 000 解析　作出函数简图如图： 三角函数模型为 y＝Asin(ωx＋φ)＋B， 由题意知 A＝1 2(9 000－5 000)＝2 000，B＝7 000， T＝2×(9－3)＝12， ∴ω＝2π T ＝π 6. 将(3,9 000)看成函数图象的第二个特殊点， 则有π 6×3＋φ＝π 2，∴φ＝0， 故 f(x)＝2 000sin π 6x＋7 000(1≤x≤12，x∈N*)． ∴f(7)＝2 000×sin 7π 6 ＋7 000＝6 000(元)． 故 7 月份的出厂价格为 6 000 元． 思维升华 (1)研究 y＝Asin(ωx＋φ)的性质时可将 ωx＋φ 视为一个整体，利用换元法和数形结 合思想进行解题． (2)方程根的个数可转化为两个函数图象的交点个数． (3)三角函数模型的应用体现在两方面：一是已知函数模型求解数学问题；二是把实际问题抽 象转化成数学问题，利用三角函数的有关知识解决问题． 跟踪训练 3 (1)已知函数 f(x)＝sin(ωx＋φ)(ω > 0，－π 2 ≤ φ ≤ π 2)的图象上的两个相邻的最高 点和最低点的距离为 2 2，且过点(2，－1 2)，则函数 f(x)的解析式为______________． 答案　f(x)＝sin(πx 2 ＋π 6) 解析　根据已知两个相邻最高点和最低点的距离为 2 2，可得 (T 2 )2＋(1＋1)2＝2 2， 解得 T＝4， 故 ω＝2π T ＝π 2，即 f(x)＝sin(πx 2 ＋φ). 又函数图象过点(2，－1 2)， 故 f(2)＝sin(π 2 × 2＋φ)＝－sin φ＝－1 2， 又－π 2≤φ≤π 2，解得 φ＝π 6， 故 f(x)＝sin(πx 2 ＋π 6). (2)(2019·江苏省淮海中学测试)已知函数 f(x)＝4sin x·cos (x＋π 3 )＋ 3. ①求 f(x)在区间[－π 4，π 6]上的最大值和最小值及取得最值时 x 的值； ②若方程 f(x)－t＝0 在 x∈[－π 4，π 2]上有唯一解，求实数 t 的取值范围． 解　①f(x)＝4sin x(cos xcosπ 3－sin xsinπ 3)＋ 3 ＝2sin xcos x－2 3sin2x＋ 3 ＝sin 2x＋ 3cos 2x ＝2sin(2x＋π 3). 因为－π 4≤x≤π 6，所以－π 6≤2x＋π 3≤2π 3 ， 所以－1 2≤sin(2x＋π 3)≤1，所以－1≤f(x)≤2， 当 2x＋π 3＝－π 6，即 x＝－π 4时，f(x)min＝－1； 当 2x＋π 3＝π 2，即 x＝ π 12时，f(x)max＝2. ②因为当－π 4≤x≤ π 12时，－π 6≤2x＋π 3≤π 2， 所以－1≤2sin(2x＋π 3)≤2，且单调递增； 当 π 12≤x≤π 2时，π 2≤2x＋π 3≤4π 3 ， 所以－ 3≤2sin(2x＋π 3)≤2，且单调递减， 所以 f(x)＝t 有唯一解时对应 t 的取值范围是 t∈[－ 3，－1)或 t＝2. 三角函数图象与性质的综合问题 例 (14 分)已知函数 f(x)＝2 3sin(x 2＋π 4 )·cos(x 2＋π 4 )－sin(x＋π)． (1)求 f(x)的最小正周期； (2)若将 f(x)的图象向右平移π 6个单位长度，得到函数 g(x)的图象，求函数 g(x)在区间[0，π]上 的最大值和最小值． 规范解答 解　(1)f(x)＝2 3sin(x 2＋π 4 )cos(x 2＋π 4 ) －sin(x＋π)＝ 3cos x＋sin x[3 分] ＝2sin(x＋π 3 )，[5 分] 于是 T＝2π 1 ＝2π.[6 分] (2)由已知得 g(x)＝f (x－π 6 )＝2sin(x＋π 6 )，[8 分] ∵x∈[0，π]，∴x＋π 6∈[π 6，7π 6 ]， ∴sin(x＋π 6 )∈[－1 2，1]，[10 分] ∴g(x)＝2sin(x＋π 6 )∈[－1,2]．[12 分] 故函数 g(x)在区间[0，π]上的最大值为 2，最小值为－1.[14 分] 解决三角函数图象与性质的综合问题的一般步骤 第一步：(化简)将 f(x)化为 asin x＋bcos x 的形式； 第二步：(用辅助角公式)构造 f(x)＝ a2＋b2·(sin x· a a2＋b2 ＋cos x· b a2＋b2)； 第三步：(求性质)利用 f(x)＝ a2＋b2sin(x＋φ)研究三角函数的性质． 1．(2018·南通模拟)在平面直角坐标系 xOy 中，将函数 y＝cos 2x 的图象向右平移 π 6个单位长 度得到 g(x)的图象，则 g (π 2 )的值为________． 答案　－1 2 解析　由题意得，将函数 y＝cos 2x 的图象向右平移π 6个单位长度，得到 g(x)＝cos (2x－π 3)的图 象， 所以 g(π 2 )＝cos(π－π 3 )＝－1 2. 2．若将函数 f(x)＝sin 2x＋cos 2x 的图象向右平移 φ 个单位长度，所得图象关于 y 轴对称， 则 φ 的最小正值是________． 答案　3π 8 解析　f(x)＝sin 2x＋cos 2x＝ 2cos(2x－π 4)，将函数 f(x)的图象向右平移 φ 个单位长度后所得 图象对应的函数为 y＝ 2cos(2x－π 4－2φ)，且该函数为偶函数， 故 2φ＋π 4＝kπ(k∈Z)，所以 φ 的最小正值为3π 8 . 3．函数 f(x)＝cos(ωx＋π 6)(ω>0)的最小正周期是 π，则其图象向右平移π 3个单位长度后对应函数 的单调递减区间是________________． 答案　[π 4＋kπ，3π 4 ＋kπ](k∈Z) 解析　由题意知 ω＝2π π ＝2，将函数 f(x)的图象向右平移π 3个单位长度后得到函数 g(x)＝cos [2(x－π 3 )＋π 6]＝cos(2x－π 2)＝sin 2x 的图象，由 2kπ＋π 2≤2x≤2kπ＋3π 2 (k∈Z)，解得所求函数的 单调递减区间为[kπ＋π 4，kπ＋3π 4 ](k∈Z)． 4．函数 f(x)＝sin(ωx＋φ) (ω > 0，|φ| < π 2)的部分图象如图所示，则 f(x)的单调递增区间为 ________． 答案　[－3＋8k,1＋8k](k∈Z) 解析　由题图知，T＝4×(3－1)＝8，所以 ω＝2π T ＝π 4， 所以 f(x)＝sin(π 4x＋φ).把(1,1)代入，得 sin(π 4＋φ )＝1，即π 4＋φ＝π 2＋2kπ(k∈Z)， 又|φ|<π 2，所以 φ＝π 4，所以 f(x)＝sin(π 4x＋π 4).由 2kπ－π 2≤π 4x＋π 4≤2kπ＋π 2(k∈Z)， 得 8k－3≤x≤8k＋1(k∈Z)， 所以函数 f(x)的单调递增区间为[8k－3,8k＋1](k∈Z)． 5．(2018·江苏泰州中学月考)将函数 y＝sin 2x 的图象向右平移 φ 个单位长度(φ>0)，使得平移 后的图象仍过点(π 3， 3 2 )，则 φ 的最小值为________． 答案　π 6 解析　将 y＝sin 2x 的图象向右平移 φ 个单位长度(φ>0)得到 y＝sin 2(x－φ)， 代入点(π 3， 3 2 )得 3 2 ＝sin(2π 3 －2φ)， 因为 φ>0，所以当2π 3 －2φ＝π 3时，第一个正弦值为 3 2 的角，此时 φ 最小，为π 6. 6．将函数 f(x)＝sin(2x＋φ)(|φ| < π 2)的图象向左平移π 6个单位长度后关于原点对称，则函数 f(x) 在[0，π 2 ]上的最小值为________． 答案　－ 3 2 解析　将函数 f(x)＝sin(2x＋φ)的图象向左平移 π 6个单位长度得到 y＝sin[2(x＋π 6 )＋φ]＝sin (2x＋π 3＋φ)的图象，该图象关于原点对称，即为奇函数，则π 3＋φ＝kπ(k∈Z)， 又|φ|<π 2，所以 φ＝－π 3，即 f(x)＝sin(2x－π 3). 当 x∈[0，π 2 ]时，2x－π 3∈[－π 3，2π 3 ]， 所以当 2x－π 3＝－π 3，即 x＝0 时，f(x)取得最小值，最小值为－ 3 2 . 7.已知函数 f(x)＝Atan(ωx＋φ)(ω > 0，|φ| < π 2)的部分图象如图所示，则 f ( π 24 )＝________. 答案　 3 解析　由题干图象知π ω＝2×(3π 8 －π 8)＝π 2， 所以 ω＝2. 因为 2×π 8＋φ＝kπ＋π 2(k∈Z)， 所以 φ＝kπ＋π 4(k∈Z)， 又|φ|<π 2，所以 φ＝π 4， 这时 f(x)＝Atan(2x＋π 4). 又函数图象过点(0,1)，代入上式得 A＝1，所以 f(x)＝tan(2x＋π 4). 所以 f( π 24 )＝tan(2 × π 24＋π 4)＝ 3. 8.已知函数 f(x)＝sin(ωx＋φ)(ω > 0，|φ| < π 2)的部分图象如图所示，又 x1，x2∈(－π 6，π 3)，且 f(x1) ＝f(x2)，则 f(x1＋x2)＝________. 答案　 3 2 解析　由题图可知，T 2＝π 3－(－π 6 )＝π 2， 则 T＝π，ω＝2，又 －π 6＋π 3 2 ＝ π 12， 所以 f(x)的图象过点( π 12，1)， 即 sin(2 × π 12＋φ)＝1， 所以 2× π 12＋φ＝π 2＋2kπ，k∈Z， 又|φ|<π 2，可得 φ＝π 3，所以 f(x)＝sin(2x＋π 3). 由 f(x1)＝f(x2)，x1，x2∈(－π 6，π 3)， 可得 x1＋x2＝－π 6＋π 3＝π 6， 所以 f(x1＋x2)＝f (π 6 )＝sin(2 × π 6＋π 3)＝sin2π 3 ＝ 3 2 . 9．(2018·南京模拟)在同一直角坐标系中，函数 y＝sin (x＋π 3 )(x∈[0,2π])的图象和直线 y＝1 2 的交点的个数是________． 答案　2 解析　方法一　令 sin(x＋π 3 )＝1 2，可得 x＋π 3＝2kπ＋π 6或 x＋π 3＝2kπ＋5π 6 ，k∈Z， 即 x＝2kπ－π 6或 x＝2kπ＋π 2，k∈Z，又 x∈[0,2π]，所以 x＝11π 6 或 x＝π 2， 故原函数图象与 y＝1 2的交点的个数是 2. 方法二　在同一个坐标系下画出这两个函数图象，可得交点个数为 2. 10．已知函数 f(x)＝cos(3x＋π 3)，其中 x∈[π 6，m ]，若 f(x)的值域是[－1，－ 3 2 ]，则 m 的取值 范围是________． 答案　[2π 9 ，5π 18] 解析　画出函数的图象如图所示． 由 x∈[π 6，m ]，可知5π 6 ≤3x＋π 3≤3m＋π 3， 因为 f(π 6 )＝cos 5π 6 ＝－ 3 2 且 f(2π 9 )＝cos π＝－1，要使 f(x)的值域是[－1，－ 3 2 ]， 只要2π 9 ≤m≤5π 18，即 m∈[2π 9 ，5π 18]. 11．已知函数 f(x)＝2sin(2ωx＋π 6)(其中 0<ω<1)，若点(－π 6，0)是函数 f(x)图象的一个对称中 心． (1)求 ω 的值，并求出函数 f(x)的单调递增区间； (2)先列表，再作出函数 f(x)在区间[－π，π]上的图象． 解　(1)因为点(－π 6，0)是函数 f(x)图象的一个对称中心， 所以－ωπ 3 ＋π 6＝kπ(k∈Z)，ω＝－3k＋1 2(k∈Z)， 因为 0<ω<1，所以当 k＝0 时，可得 ω＝1 2. 所以 f(x)＝2sin(x＋π 6 ). 令 2kπ－π 2≤x＋π 6≤2kπ＋π 2(k∈Z)， 解得 2kπ－2π 3 ≤x≤2kπ＋π 3(k∈Z)， 所以函数的单调递增区间为[2kπ－2π 3 ，2kπ＋π 3](k∈Z)． (2)由(1)知，f(x)＝2sin(x＋π 6 )，x∈[－π，π]， 列表如下： x＋π 6 －5π 6 －π 2 0 π 2 π 7π 6 x －π －2π 3 －π 6 π 3 5π 6 π f(x) －1 －2 0 2 0 －1 作出函数部分图象如图所示： 12．设函数 f(x)＝sin(ωx－π 6)＋sin(ωx－π 2)，其中 0<ω<3.已知 f (π 6 )＝0. (1)求 ω； (2)将函数 y＝f(x)的图象上各点的横坐标伸长为原来的 2 倍(纵坐标不变)，再将得到的图象向 左平移π 4个单位长度，得到函数 y＝g(x)的图象，求 g(x)在[－π 4，3π 4 ]上的最小值． 解　(1)因为 f(x)＝sin(ωx－π 6)＋sin(ωx－π 2)， 所以 f(x)＝ 3 2 sin ωx－1 2cos ωx－cos ωx ＝ 3 2 sin ωx－3 2cos ωx＝ 3(1 2sin ωx－ 3 2 cos ωx) ＝ 3sin(ωx－π 3). 由题设知 f (π 6 )＝0， 所以ωπ 6 －π 3＝kπ，k∈Z， 故 ω＝6k＋2，k∈Z.又 0<ω<3， 所以 ω＝2. (2)由(1)得 f(x)＝ 3sin(2x－π 3)， 所以 g(x)＝ 3sin(x＋π 4－π 3)＝ 3sin(x－ π 12). 因为 x∈[－π 4，3π 4 ]， 所以 x－ π 12∈[－π 3，2π 3 ]， 当 x－ π 12＝－π 3，即 x＝－π 4时，g(x)取得最小值－3 2. 13．将函数 f(x)＝sin(2x＋θ)(－π 2 < θ < π 2)的图象向右平移 φ(0<φ<π)个单位长度后，得到函数 g(x) 的图象，若 f(x)，g(x)的图象都经过点 P(0， 3 2 )，则 φ 的值为________． 答案　5π 6 解析　g(x)＝sin[2(x－φ)＋θ]＝sin(2x－2φ＋θ)， 若 f(x)，g(x)的图象都经过点 P(0， 3 2 )， 所以 sin θ＝ 3 2 ，sin(－2φ＋θ)＝ 3 2 ， 又－π 2<θ<π 2， 所以 θ＝π 3，sin(π 3－2φ)＝ 3 2 . 又 0<φ<π，所以－5π 3 <π 3－2φ<π 3， 所以π 3－2φ＝－4π 3 . 即 φ＝5π 6 . 14．已知函数 f(x)＝ 3sin ωx＋cos ωx(ω>0)，x∈R.在曲线 y＝f(x)与直线 y＝1 的交点中，若 相邻交点距离的最小值为π 3，则 f(x)的最小正周期为________． 答案　π 解析　f(x)＝ 3sin ωx＋cos ωx＝2sin(ωx＋π 6)(ω>0)． 由 2sin(ωx＋π 6)＝1，得 sin(ωx＋π 6)＝1 2， ∴ωx＋π 6＝2kπ＋π 6或 ωx＋π 6＝2kπ＋5π 6 (k∈Z)． 令 k＝0，得 ωx1＋π 6＝π 6，ωx2＋π 6＝5π 6 ， ∴x1＝0，x2＝2π 3ω. 由|x1－x2|＝π 3，得2π 3ω＝π 3，∴ω＝2. 故 f(x)的最小正周期 T＝2π 2 ＝π. 15．已知函数 y＝Msin(ωx＋φ)(M>0，ω>0,0<φ<π)的图象关于直线 x＝ 1 3对称．该函数的部分 图象如图所示，AC＝BC＝ 2 2 ，C＝90°，则 f (1 2 )的值为________． 答案　 3 4 解析　依题意知，△ABC 是直角边长为 2 2 的等腰直角三角形， 因此其边 AB 上的高是1 2，函数 f(x)的最小正周期是 2， 故 M＝1 2，2π ω＝2，ω＝π，f(x)＝1 2sin(πx＋φ)． 又 f(x)的图象关于直线 x＝1 3对称， ∴f (1 3 )＝1 2sin(π 3＋φ )＝±1 2. ∴π 3＋φ＝kπ＋π 2，k∈Z，又 0<φ<π， ∴φ＝π 6， ∴f (1 2 )＝1 2sin(π 2＋π 6 )＝ 3 4 . 16．已知函数 f(x)＝Asin(2x＋φ)－1 2(A > 0，0 < φ < π 2)的图象在 y 轴上的截距为 1，且关于直线 x＝ π 12对称，若存在 x∈[0，π 2 ]，使 m2－3m≥f(x)成立，则实数 m 的取值范围为______________． 答案　(－∞，1]∪[2，＋∞) 解析　∵函数 f(x)＝Asin(2x＋φ)－1 2(A > 0，0 < φ < π 2)的图象在 y 轴上的截距为 1， ∴Asin φ－1 2＝1，即 Asin φ＝3 2. ∵函数 f(x)＝Asin(2x＋φ)－1 2的图象关于直线 x＝ π 12对称， ∴2× π 12＋φ＝kπ＋π 2，k∈Z， 又 0<φ<π 2，∴φ＝π 3，∴A·sinπ 3＝3 2， ∴A＝ 3，∴f(x)＝ 3sin(2x＋π 3)－1 2. 当 x∈[0，π 2 ]时，2x＋π 3∈[π 3，4π 3 ]， ∴当 2x＋π 3＝4π 3 ，即 x＝π 2时， f(x)min＝－3 2－1 2＝－2. 令 m2－3m≥－2，解得 m≥2 或 m≤1.