九年级数学上册第一章特殊平行四边形专题课堂一特殊平行四边形的应用课件新版北师大版

九年级数学上册第一章特殊平行四边形专题课堂一特殊平行四边形的应用课件新版北师大版

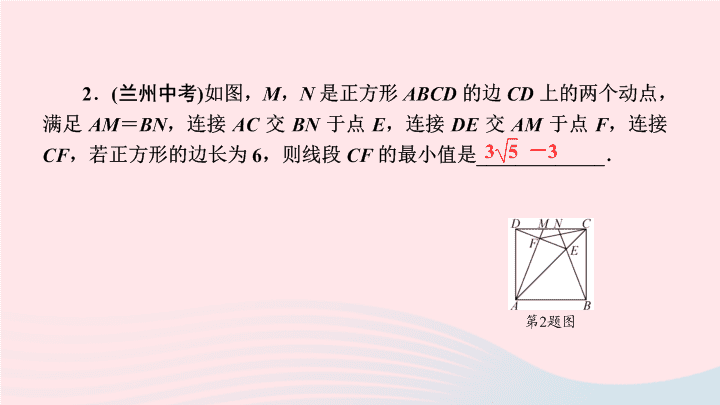
第一章　特殊平行四边形 专题课堂(一)　特殊平行四边形的应用 1 ．如图，正方形 ABCD 的边长为 2 ，将长为 2 的线段 QR 的两端放在正方形的相邻的两边上同时滑动．如果点 Q 从点 A 出发，沿图中所示方向按 A → B → C → D → A 滑动到点 A 停止，同时点 R 从点 B 出发，沿图中所示方向按 B → C → D → A → B 滑动到点 B 停止，在这个过程中，线段 QR 的中点 M 所经过的路线与正方形 ABCD 所围成的图形的面积为 ( ) A ． 2 B ． 4 － π C ． π D ． π － 1 B 3 ．如图，在菱形 ABCD 中， AB ＝ 2 ，∠ DAB ＝ 60° ， E 是 AD 边的中点， M 是 AB 边上一动点 ( 不与点 A 重合 ) ，延长 ME 交射线 CD 于点 N ，连接 MD ， AN . (1) 求证：四边形 AMDN 是平行四边形； (2) 填空：①当 AM 的值为 ________ 时，四边形 AMDN 是矩形； ②当 AM 的值为 ________ 时，四边形 AMDN 是菱形． 解： (1)∵ 四边形 ABCD 是菱形，∴ ND ∥ AM ，∴∠ NDE ＝∠ MAE ，∠ DNE ＝∠ AME . 又∵ E 是 AD 的中点，∴ DE ＝ AE ，∴△ NDE ≌△ MAE ，∴ ND ＝ MA ，∴四边形 AMDN 是平行四边形　 (2)①1 　② 2 4 ．如图，△ ABC 是等腰直角三角形，∠ BAC ＝ 90° ， P ， Q 分别是 AB ， AC 上的动点，且满足 BP ＝ AQ ， D 是 BC 的中点，连接 AD . (1) 求证：△ PDQ 是等腰直角三角形； (2) 当点 P 运动到什么位置时，四边形 APDQ 是正方形？请说明理由． 解： (1)∵△ ABC 是等腰直角三角形， D 是 BC 的中点，∴ AD ⊥ BC ， BD ＝ AD ＝ DC ，∠ B ＝∠ DAQ . 又∵ BP ＝ AQ ，∴△ BPD ≌△ AQD ，∴ PD ＝ QD ，∠ BDP ＝∠ ADQ .∵∠ BDP ＋∠ ADP ＝ 90° ，∴∠ ADQ ＋∠ ADP ＝∠ PDQ ＝ 90° ，∴△ PDQ 是等腰直角三角形 A 7 ． (2019 · 贺州 ) 如图，在矩形 ABCD 中， E ， F 分别是 BC ， AD 边上的点，且 AE ＝ CF . (1) 求证：△ ABE ≌△ CDF ； (2) 当 AC ⊥ EF 时，四边形 AECF 是菱形吗？请说明理由． (2) 当 AC ⊥ EF 时，四边形 AECF 是菱形，理由：∵△ ABE ≌△ CDF ，∴ BE ＝ DF ，∵ BC ＝ AD ，∴ CE ＝ AF ，∵ CE ∥ AF ，∴四边形 AECF 是平行四边形，又∵ AC ⊥ EF ，∴四边形 AECF 是菱形 8 ． (2019 · 鄂州 ) 如图，在矩形 ABCD 中， AB ＝ 8 ， AD ＝ 6 ，点 O 是对角线 BD 的中点，过点 O 的直线分别交 AB ， CD 边于点 E ， F . (1) 求证：四边形 DEBF 是平行四边形； (2) 当 DE ＝ DF 时，求 EF 的长． (1) 证明：∵四边形 ABCD 是矩形，∴ AB ∥ CD ，∴∠ DFO ＝∠ BEO ，又因为∠ DOF ＝∠ BOE ， OD ＝ OB ，∴△ DOF ≌△ BOE (AAS) ，∴ DF ＝ BE ，又∵ DF ∥ BE ，∴四边形 BEDF 是平行四边形 A 10 ． (2019 · 黄石 ) 如图，在平面直角坐标系中，边长为 2 的正方形 ABCD 的边 AB 在 x 轴上， AB 边的中点是坐标原点 O ，将正方形绕点 C 按逆时针方向旋转 90° 后，点 B 的对应点 B ′ 的坐标是 ( ) A ． ( － 1 ， 2) B ． (1 ， 4) C ． (3 ， 2) D ． ( － 1 ， 0) C 11 ．如图，四边形 ABCD 是正方形， G 是 BC 边上任意一点， DE ⊥ AG 于点 E ， BF ∥ DE 交 AG 于点 F . (1) 求证： AF － BF ＝ EF ； (2) 将△ ABF 绕点 A 逆时针旋转，使得 AB 与 AD 重合，记此时点 F 的对应点为点 F ′ ，若正方形 ABCD 的边长为 3 ，求点 F ′ 与旋转前图中点 E 之间的距离． (2) 如图，根据题意知∠ FAF ′ ＝ 90°. 又∵∠ AED ＝ 90° ，∠ AF ′ D ＝∠ AFB ＝ 90° ，∴四边形 AEDF ′ 为矩形，∴ EF ′ ＝ AD ＝ 3. 即点 F ′ 与旋转前图中点 E 之间的距离为 3