北京市人大附中2020届高三(6月份)高考数学考前热身试题 Word版含解析
2020年北京市人大附中高考数学考前热身试卷(6月份)
一、选择题(共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.)
1. 已知集合,,则( )
A. B. C. D.
【答案】B
【解析】
【分析】
先求解集合再求并集即可.
【详解】,.
故.
故选:B
【点睛】本题主要考查了集合的基本运算与绝对值不等式的求解.属于基础题型.
2. 复数的模为( )
A. 1 B. 2 C. D.
【答案】A
【解析】
【分析】
根据复数的除法运算化简再求模长即可.
【详解】.模长为1.
故选:A
【点睛】本题主要考查了复数的除法与模长的计算.属于基础题型.
3. 若a>0,b>0,则不等式-b<
D. x<-或x>
【答案】D
【解析】
试题分析:根据题意分类讨论,当时,只需,所以,当时,只需,所以,因此的解是或,故选D.
考点:1、分式不等式;2、分类讨论;3、不等式的恒成立.
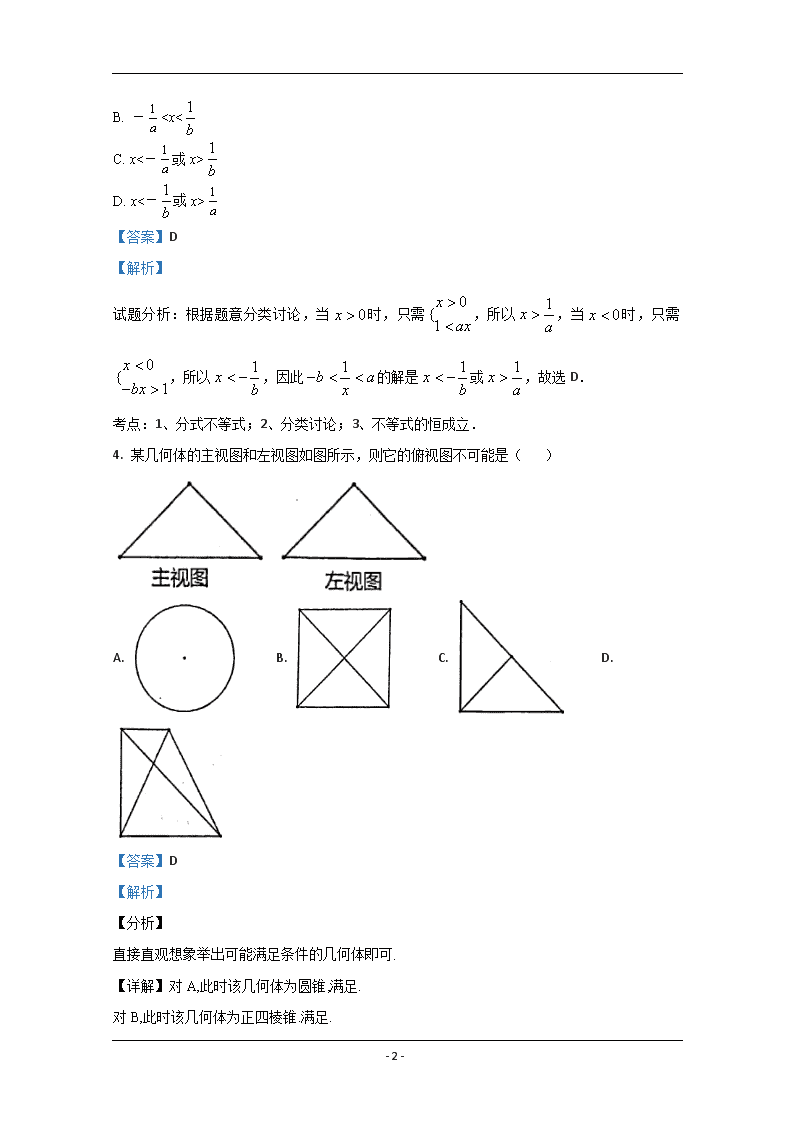
4. 某几何体的主视图和左视图如图所示,则它的俯视图不可能是( )
A. B. C. D.
【答案】D
【解析】
【分析】
直接直观想象举出可能满足条件的几何体即可.
【详解】对A,此时该几何体为圆锥,满足.
对B,此时该几何体为正四棱锥.满足.
- 23 -
对C,此时该几何体为正四棱锥的一半.满足.
故选:D
【点睛】本题主要考查了直观想象能力与三视图的辨析.属于基础题型.
5. 某公司为激励创新,计划逐年加大研发资金投入,若该公司2018年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是( )
(参考数据:lg1.12≈0.05,lg1.3≈0.11,lg2≈0.30)
A. 2020年 B. 2021年 C. 2022年 D. 2023年
【答案】C
【解析】
【详解】根据题意,设第年开始超过200万元,
则,
化为:,
解可得:;
则.
故选:C.
【点睛】本题考查函数的应用,涉及对数的计算,属于基础题.
6. 为非零向量,“”为“共线”的()
A. 充分必要条件 B. 充分不必要条件
C. 必要不充分条件 D. 即不充分也不必要条件
【答案】B
【解析】
【分析】
共线,方向相同或相反,共线的单位向量不一定相等,结合充分必要条件的判断,即可得出结论.
【详解】分别表示与同方向的单位向量,
- 23 -
,则有共线,
而共线,则是相等向量或相反向量,
“”为“共线”的充分不必要条件.
故选:B.
【点睛】本题考查命题充分不必要条件的判定,考查共线向量和单位向量的间的关系,属于基础题.
7. 已知函数(其中)的最小值为1,则( )
A. 1 B. C. D.
【答案】A
【解析】
【分析】
根据题意分析当时分别取得最小值再求解即可.
【详解】由题,因为在时取最小值,
又当且仅当时成立.
故当时取最小值.解得.
故选:A
【点睛】本题主要考查了二次函数与基本不等式求最小值的问题,属于中等题型.
8. 已知函数,若函数在区间内没有零点,则的最大值是( )
A. B. C. D.
【答案】C
【解析】
【分析】
- 23 -
利用三角恒等变换化简,结合正弦函数图象,即可求解.
详解】,
令,
函数在区间内没有零点,
解得,
,
的最大值是.
故选:C.
【点睛】本题考查三角函数恒等变换化简,以及三角函数的性质,意在考查直观想象、逻辑推理能力,属于中档题.
9. 已知不过坐标原点的直线交抛物线于,两点,若直线,的斜率分别为2和6,则直线的斜率为( )
A. 3 B. 2 C. -2 D. -3
【答案】D
【解析】
设,,那么 ,所以,而 ,故,,所以,,选.
10. 2016年“一带一路”沿线64个国家GDP之和约为12.0万亿美元,占全球GDP的;人口总数约为32.1亿,占全球总人口的;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的.
2016年“一带一路”沿线国家情况
- 23 -
人口(万人)
GDP(亿美元)
进口额(亿美元)
出口额(亿美元)
蒙古
301.4
116.5
38.7
45.0
东南亚11国
63852.5
25802.2
11267.2
11798.6
南亚8国
174499.0
29146.6
4724.1
3308.5
中亚5国
6946.7
2254.7
422.7
590.7
西亚、北非19国
43504.6
36467.5
9675.5
8850.7
东欧20国
32161.9
26352.1
9775.5
11388.4
关于“一带一路”沿线国家2016年状况,能够从上述资料中推出的是( )
A. 超过六成人口集中在南亚地区
B. 东南亚和南亚国家GDP之和占全球的以上
C. 平均每个南亚国家对外贸易额超过1000亿美元
D. 平均每个东欧国家的进口额高于平均每个西亚、北非国家的进口额
【答案】C
【解析】
【分析】
利用表中所给的数据对四个选项逐一判断即可.
【详解】A:南亚地区人口总数为174499.0万人,“一带一路”沿线国家人口总数为:321266.1万人,所以,故本选项说法不正确的;
B:东南亚和南亚国家GDP之和54948.8亿美元,“一带一路”沿线国家GDP之和120139.6亿美元,所以,所以东南亚和南亚国家GDP之和占“一带一路”沿线国家GDP之和的,因此东南亚和南亚国家GDP之和占全球的,故本选项说法是不正确的;
C:南亚国家对外贸易额平均值为:,故本选项说法是正确的;
- 23 -
D:平均每个东欧国家的进口额为:,平均每个西亚、北非国家的进口额为:,故本选项说法是不正确的.
故选:C
【点睛】本题考查了根据数据对一些说法进行判断,考查了平均数的求法,考查了数学阅读能力.
二、填空题(共5小题,每小题5分,共25分.)
11. 在的展开式中,项的系数是__________(用数字作答).
【答案】
【解析】
的展开式的通项为:.
令,得.
答案为:-40.
点睛:求二项展开式有关问题的常见类型及解题策略
(1)求展开式中的特定项.可依据条件写出第r+1项,再由特定项的特点求出r值即可.
(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,再由通项写出第r+1项,由特定项得出r值,最后求出其参数.
12. 双曲线:的离心率为______,双曲线与双曲线有共同的渐近线,且过点,则双曲线的方程为______.
【答案】 (1). (2).
【解析】
【分析】
(1)根据离心率的定义与的关系求解即可.
(2)设的方程为,再代入求解即可.
- 23 -
【详解】(1)由题,双曲线,故离心率.
(2) 设的方程为,代入有.
故方程.
故答案为:(1). (2).
【点睛】本题主要考查了双曲线的基本量求法以及共渐近线的双曲线的求法等.属于基础题型.
13. 锐角三角形中,若,则的范围是 ;
【答案】(
【解析】
试题分析:因为,为锐角三角形,
所以
根据正弦定理,根据余弦函数的图象,可知
考点:本小题主要考查正弦定理、二倍角公式以及三角函数图象的性质和应用,考查学生的转化能力和数
形结合思想的应用.
点评:解决此题时,容易漏掉,从而产生错误结论,所以解题时一定要严谨.
14. 已知非零向量,满足,.若,则实数的值为______.
【答案】-4
【解析】
【分析】
根据垂直数量积为0与数量积运算求解即可.
- 23 -
【详解】由可得.
故.
故答案为:
【点睛】本题主要考查了向量垂直的数量积运算,属于基础题型.
15. 已知函数.
(1)的零点是______;
(2)若的图象与直线有且只有三个公共点,则实数的取值范围是______.
【答案】 (1). 1和 (2).
【解析】
【分析】
(1)分段求解零点即可.
(2)数形结合画出分析其与直线有三个交点的情况即可.
【详解】(1)由,当时,.
当时,令有
(2)画出的图象有
- 23 -
因为过定点(0,−1),
要使的图象与直线有且只有三个公共点,则,
当时,函数的导数,函数在点(0,−1)处的切线斜率
,此时直线和只有一个交点.
当时,因为当时,,此时直线与的图象仍有三个交点.由图象知要使的图象与直线有且只有三个公共点,
则满足,
故答案为:(1). 或 (2). (0,2)
【点睛】本题主要考查了函数零点问题的应用,同时也考查了数形结合求解直线与函数的零点个数问题,需要利用求导求斜率分析直线与曲线的相交情况,属于中等题型.
三、解答题(共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.)
16. 设函数,其中.已知.
(Ⅰ)求;
(Ⅱ)将函数的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数的图象,求在上的最小值.
【答案】(Ⅰ) .
(Ⅱ) .
【解析】
试题分析:(Ⅰ)利用两角和与差的三角函数化简得到
由题设知及可得.
(Ⅱ)由(Ⅰ)得
从而.
根据得到,进一步求最小值.
- 23 -
试题解析:(Ⅰ)因为,
所以
由题设知,
所以,.
故,,又,
所以.
(Ⅱ)由(Ⅰ)得
所以.
因为,
所以,
当,
即时,取得最小值.
【名师点睛】此类题目是三角函数问题中的典型题目,可谓相当经典.解答本题,关键在于能利用三角公式化简函数、进一步讨论函数的性质,本题易错点在于一是图象的变换与解析式的对应,二是忽视设定角的范围.难度不大,能较好的考查考生的基本运算求解能力及复杂式子的变形能力等.
17. 为了解学生自主学习期间完成数学套卷的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
- 23 -
(1)从这班学生中任选一名男生,一名女生,求这两名学生完成套卷数之和为4的概率?
(2)若从完成套卷数不少于4套的学生中任选4人,设选到的男学生人数为,求随机变量的分布列和数学期望;
(3)试判断男学生完成套卷数方差与女学生完成套卷数的方差的大小(只需写出结论).
【答案】(1)(2)详见解析(3)
【解析】
【分析】
(1)根据组合的方法求解所有可能的情况与满足条件的情况数再计算概率即可.
(2)的取值为0,1,2,3,4.再根据超几何分布的方法求分布列与数学期望即可.
(3)直接根据数据观察稳定性判断与的大小即可.
【详解】解:(1)设事件:从这个班级的学生中随机选取一名男生,一名女生,这两名学生完成套卷数之和为4,
由题意可知,.
(2)完成套卷数不少于4本的学生共8人,其中男学生人数为4人,故的取值为0,1,2,3,4.
由题意可得;
;
;
;
- 23 -
.
所以随机变量的分布列为
0
1
2
3
4
随机变量的均值.
(3).
【点睛】本题主要考查了排列组合解决概率的问题与超几何分布的分布列与均值的求解.属于中等题型.
18. 平行四边形所在的平面与直角梯形所在的平面垂直,,,且,,,为的中点.
(1)求证:平面;
(2)求证:;
(3)若直线上存在点,使得,所成角的余弦值为,求与平面所成角的大小.
【答案】(1)证明见解析(2)证明见解析(3)
【解析】
- 23 -
【分析】
(1)取的中点或取中点,利用证平行四边形的方法再证明平面即可.
(2)根据勾股定理与余弦定理证明,再根据面面垂直的性质得出平面即可证明.
(3) 以、、所在直线为、、轴建立空间直角坐标系.
设,再利用空间向量求解关于线面角的问题即可.
【详解】(1)解法1:取的中点,连结,,,
在直角梯形中,,,
所以四边形为平行四边形,
所以,
在中,,
所以,
又因为,
所以平面平面,
又平面,
所以平面.
解法2:取中点,连结,,
在中,,,
- 23 -
所以,且,
又,,
所以,,
所以四边形为平行四边形,
所以,
因为平面,平面,
所以平面.
(2)在中,,,
所以,
所以,
所以,
又平面平面,平面平面,平面,
所以平面,
因为平面,
所以.
(3)由(1)(2)以为原点,以、、所在直线为、、轴建立空间直角坐标系.
所以,,,,,
所以,
所以,,,
- 23 -
设,
所以,
所以,
所以,
所以,
所以,
设平面的法向量为,
所以,
所以令,则,
如与平面成的角为,
所以.
所以,即与面成的角为.
【点睛】本题主要考查了线面平行与线线垂直的一般方法,同时也考查了建立空间直角坐标系求解线面角的问题,需要设线段的比例关系,
- 23 -
求解关于比例参数的解析式根据线面角大小化简求解.属于难题.
19. 已知椭圆:离心率为,过的左焦点做轴的垂线交椭圆于、两点,且.
(1)求椭圆的标准方程及长轴长;
(2)椭圆的短轴的上下端点分别为,,点,满足,且,若直线,分别与椭圆交于,两点,且面积是面积的5倍,求的值.
【答案】(1)椭圆的标准方程为:,长轴长为4(2)
【解析】
【分析】
(1)根据通径与椭圆的基本量的关系求解即可.
(2)分别设直线,直线的方程,联立椭圆的方程,再利用三角形的面积公式表达出面积是面积的5倍,再代入韦达定理求解即可.
【详解】解:(1)因为椭圆的左焦点横坐标为,
由及,得,
故,又,解得:,
所以,椭圆的标准方程为:,长轴长为4.
(2)∵,,,且,
∴直线的斜率为,直线斜率为,
∴直线的方程为,直线的方程为,
- 23 -
由得,∴,,∴,
由得,∴,,∴;
∵,
,
,,
∴,
即,
又,
∴,
整理方程得:,
解得:.
【点睛】本题主要考查了椭圆中基本量的运算以及直线与椭圆相交求面积的方法等.需要联立方程求解对应的面积表达式,代入韦达定理化简求得参数.属于难题.
20. 已知函数.
- 23 -
(1)求函数的单调区间;
(2)若对任意,都有成立,求实数的最小值.
【答案】(1)函数的单增区间为,单减区间为(2)的最小值为1
【解析】
【分析】
(1)求导后列表分析函数单调性即可.
(2)由(1)可知的最小值为,再根据恒成立问题的方法分情况分析的最小值即可.
【详解】解:(1)由解得,
则及的情况如下:
2
-
0
+
极小值
所以函数的单增区间为,单减区间为;
(2)法一:
当时,.
当时,.
若,由(1)可知的最小值为,的最大值为,
所以“对任意,有恒成立”
等价于“”,
即,
解得.
- 23 -
所以的最小值为1.
法二:
当时,.
当时,.
且由(1)可知,的最小值为,
若,即时,
令,则任取,
有,
所以对成立,
所以必有成立,所以,即.
而当时,,,,
所以,即满足要求,
而当时,求出的的值,显然大于1,
综上,的最小值为1.
【点睛】本题主要考查了根据导数求函数的单调性与利用导数求解恒成立的有关问题,需要求导后分情况讨论函数的最值.属于中等题型.
21. 若无穷数列满足:是正实数,当时,,则称是“Y﹣数列”.
(Ⅰ)若是“Y﹣数列”且,写出的所有可能值;
(Ⅱ)设是“Y﹣数列”,证明:是等差数列当且仅当单调递减;是等比数列当且仅当单调递增;
(Ⅲ)若是“Y﹣数列”且是周期数列(即存在正整数T,使得对任意正整数n,都有),求集合的元素个数的所有可能值的个数.
【答案】(Ⅰ);(Ⅱ)证明见解析;(Ⅲ)1009.
- 23 -
【解析】
【分析】
(Ⅰ)利用递推关系,根据分类讨论思想求解即可;
(Ⅱ)当是等差数列时,利用反证法可证明单调递减,根据等比性质可证后者;
(Ⅲ)先证是数列的最大项,再证明当是奇数时,是的奇数倍,当是偶数时,是的偶数倍,即可求出.
【详解】(Ⅰ)由题可知,则或2,
,
当时,,则或,
当时,,则或4,
,
当时,,则或,
当时,,则或2,
当时,,则或2,
当时,,则或8,
综上,的所有可能值为;
(Ⅱ),或,
当是等差数列时,假设,则,
此时,而,矛盾,
,于是公差,
单调递减,
当单调递减时,对任意,,
又,,
- 23 -
是等差数列;
当是等比数列时,,,
公比,又,单调递增,
当单调递增时,对任意,,
又,
,即,
,是等比数列,
综上,是等差数列当且仅当单调递减;是等比数列当且仅当单调递增;
(Ⅲ)先证是数列的最大项,
事实上,如果是第一个大于的项的脚标,则由知,是的倍数,
假设都是的倍数,
则由知,是的倍数,
所以由归纳法知,对任意,都是的倍数,但不是的倍数,这与是周期数列矛盾,
所以是数列的最大项,从而当时,,
再证明当是奇数时,是的奇数倍;当是偶数时,是的偶数倍,
事实上,当时结论成立,假设时成立,当时,由知,结论也成立,
所以,当,的值只能是奇数,所以集合的元素个数最多有1009个;
下证集合的元素个数可以是的所有整数,
事实上,对于,可取数列为:
- 23 -
即:所有的奇数项均等于,所有的偶数项均等于0,此时,数列为“Y﹣数列”,且,
对于任意整数,构造数列的前2018项如下:
,
由于数列是无穷数列,故可取,显然满足数列是“Y﹣数列”,
综上,集合的元素个数的所有可能值的个数是1009.
【点睛】本题考查递推关系的综合应用以及反证法证明,属于难题.
- 23 -