高二数学下学期期末联考试题理新人教A版

高二数学下学期期末联考试题理新人教A版

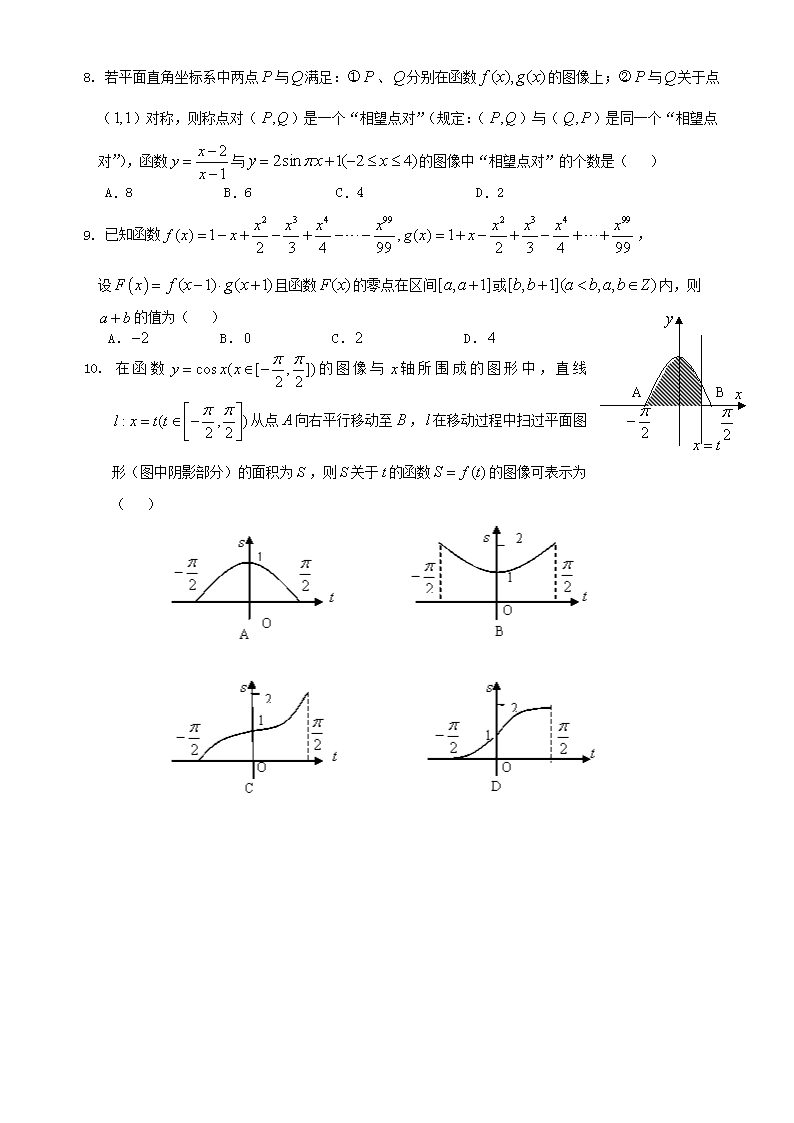
高二下学期期末联考数学（理）试题 一、选择题：本大题共 10 小题，每小题 5 分，共 50 分.在每小题给出的四个选项中,只有一项是符合题 目要求的. 1．已知全集U R ，集合 2{ | 10 9}A x y x x     ，集合 3{ | log , },B y y x x A   则 ( )UA C B = （ ） A． 1,2 B． 1,3 C. (2,9] D． (3,9] 2．设i 为虚数单位，若复数1 2 ai i   为纯虚数，则实数 a 的值为（ ） A. 1 2  B. 2 C. 1 2 D. 2 3．已知一个几何体的三视图如图所示，则该几何体的体积为（ ） A． 9 2 B．5 C．11 2 D. 6 4．设数列{ }na 的前 n 项和为 nS ，已知首项 1a  1 3 ，且对任意正整数 ,m n 都有 m n m na a a   ，若 nS k 恒成立，则实数 k 的最小值为（ ） A. 1 3 B. 1 2 C. 3 2 D. 3 5．已知 ABC 为锐角三角形，若角 终边上一点 P 的坐标为（sin cos ,cos sinA B A C  ），则 ( )f  = sin( ) cos( )2 2 | cos | | sin |         的值为 （ ） A． 2 B． 0 C． 2 D．与 的大小有关 6． 给出下列四个命题： ①已知函数 ( ) 2 2 ,x xf x   则 ( 2)y f x  的图像关于直线 2x  对称； ②平面内的动点 P 到点 ( 2,3)F  和到直线 : 2 1 0l x y   的距离相等，则点 P 的轨迹是抛物线； ③若向量 ,a b   满足 0,a b   则 a  与b  的夹角为钝角； ○4 存在 0 (1,2),x  使得 02 0 0 0( 3 2) 3 4 0xx x e x     成立，其中正确命题的个数是（ ） A．0 B．1 C．2 D．3 7．已知点 P 是曲线 2 2: 14 xC y  上的任意一点，直线 : 2l x  与双曲线C 的渐近线交于 ,A B 两点， 若 ,( , ,OP OA OB R        O 为坐标原点），则下列不等式恒成立的是（ ） A． 2 2 1 2    B． 2 2 2   C． 2 2 1 2    D． 2 2 2   8. 若平面直角坐标系中两点 P 与Q 满足：○1 P 、Q 分别在函数 ( ), ( )f x g x 的图像上；○2 P 与Q 关于点 2 1 3 俯视图 1 1 主视图 左视图 （1,1）对称，则称点对（ ,P Q ）是一个“相望点对”（规定：（ ,P Q ）与（ ,Q P ）是同一个“相望点 对”），函数 2 1 xy x   与 2sin 1( 2 4)y x x     的图像中“相望点对”的个数是（ ） A．8 B．6 C．4 D．2 9. 已知函数 2 3 4 99 2 3 4 99 ( ) 1 , ( ) 12 3 4 99 2 3 4 99 x x x x x x x xf x x g x x               ， 设  F x  ( 1) ( 1)f x g x   且函数 ( )F x 的零点在区间[ , 1]a a  或[ , 1]( , , )b b a b a b Z   内，则 a b 的值为（ ） A． 2 B． 0 C． 2 D． 4 10. 在 函 数 cos ( [ , ])2 2y x x     的 图 像 与 x 轴 所 围 成 的 图 形 中 ， 直 线 : ( , )2 2l x t t        从点 A 向右平行移动至 B ，l 在移动过程中扫过平面图 形（图中阴影部分）的面积为 S ，则 S 关于t 的函数 ( )S f t 的图像可表示为 （ ） x 2  A x t B y 2  第 II 卷 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分. 11．“求方程 5 12( ) ( ) 113 13 x x  的解”有如下解题思路：设 5 12( ) ( ) ( )13 13 x xf x   ，因为 ( )f x 在 R 上单调 递减，且 (2) 1,f  所以原方程有唯一解为 2.x  类比上述解题思路，不 等式 6 3 2(2 3) 3 2x x x x     的解集为 . 12．随机输入整数 [1,12],x 执行如右图所示的程序框图， 则输出的 x 不小 于 39 的概率为 . 13．已知点 P 是面积为 1 的 ABC 内一点（不含边界），若 ,PAB ,PBC PCA 的面积分别为 , , ,x y z 则 1y z x y z    的最小值为 . 14. 若数列{ }na 满足： 1 2 3 4 2 1 2n na a a a a a        ， 则称数列{ }na 为“正弦数列”，现将1,2,3,4,5 这五个数排成一个“正弦 数列”，所有排列种数记为 a ，则二项式 6( )ax x  的展开式中含 2x 项的系数为 ． 三、选做题：请在下列两题中任选一题作答，若两题都做，按第一题评阅计分，本题共 5 分. 15.（1）（坐标系与参数方程选做题）以平面直角坐标系的原点为极点， x 轴的正半轴为极轴，并取相等 的长度单位建立极坐标系，若直线 : cos( ) 24l     与曲线 1 4cos: 4sin 3 xC y       ( 为参数)相交 于 ,A B 两点，则线段 AB 长度为_________. （2）（不等式选做题）若存在实数 x ，使不等式 2| 2 3| | 2 1| 3x x a a     成立,则实数 a 的取值范围为 _________. 四、解答题:本大题共 6 小题，共 75 分.解答应写出文字说明、证明过程或演算步骤. 16.（本小题满分 12 分） 在 ABC 中，三个内角 , ,A B C 所对的边分别为 , ,a b c ，满足 2 22 ( )CA CB c a b     ． （1）求角C 的大小； （2）求 2 42 3 cos sin( )2 3 A B  的最大值，并求取得最大值时角 ,A B 的大小． 17.（本小题满分 12 分） 某中学为了增强学生对消防安全知识的了解，举行了一次消防知识竞赛，其中一道题是连线题，要求 将 4 种不同的消防工具与它们的 4 种不同的用途一对一连线，规定：每连对一条得 10 分，连错一条得 -5 分，某参赛者随机用 4 条线把消防工具与用途一对一全部连接起来. (1)求该参赛者恰好连对一条的概率； (2)设 X 为该参赛者此题的得分，求 X 的分布列与数学期望. 开始 结束 输入 x 输出 x 1n  3n  2 1x x  1n n  是否 18.（本小题满分 12 分） 如图所示，在边长为 3 的等边 ABC 中，点 ,D E 分别是边 ,AB AC 上的点，且满足 1 ,2 AD CE DB EA   现 将 ADE 沿 DE 折起到 1A DE 的位置，使二面角 1A DE B  成直二面角，连结 1 1,A B AC . （1）求证： 1A D BCED 平面 ； （2）在线段 BC 上是否存在点 P ，使直线 1PA 与平面 1A BD 所成的角为 60 ？ 若存在，求出 PB 的长；若不存在，请说明理由. 19.（本小题满分 12 分） 已知数列{ }na 具有性质：○1 1a 为整数；○2 对于任意的正整数 ,n 当 na 为偶数时， 1 ;2 n n aa   当 na 为奇数 时， 1 1 2 n n aa   ． （1）若 1a 为偶数，且 1 2 3, ,a a a 成等差数列，求 1a 的值； （2）若 1a 为正整数，求证：当 2 11 log ( )n a n N    时，都有 0na  ． 20.（本小题满分 13 分） 定 义 ： 在 平 面 直 角 坐 标 系 中 ， 以 原 点 为 圆 心 ， 以 2 2a b 为 半 径 的 圆 O 为 椭 圆   2 2 2 2: 1 0x yC a ba b     的“准圆”.已知椭圆 2 2 2 2: 1x yC a b   的离心率为 3 3 ，直线 : 2 5 0l x y   与椭圆C 的“准圆”相切. (1) 求椭圆C 的方程； (2) 设点 P 是椭圆C 的“准圆”上的一个动点，过动点 P 作斜率存在且不为 0 的两条不同的直线 1 2,l l ， 使得 1l ， 2l 与椭圆都相切，试判断 1l 与 2l 是否垂直？并说明理由. 21.（本小题满分 14 分） 已知函数   lnf x x ，    ag x a Rx   ，设            ,F x f x g x G x f x g x    （1） 求函数  F x 的单调区间； （2） 若以函数  ( ) (0,2)y F x x  图像上任一点  0 0,P x y 为切点的切线斜率为 1 2k  恒成立，求实 数 a 的取值范围； D B C E A1A B C D E （3） 当 1a  时 ， 对 任 意 的  1 2, 0,2x x  ， 且 1 2x x ， 已 知 存 在  0 1 2,x x x 使 得      2 1/ 0 2 1 G x G xG x x x   ，求证： 0 1 2x x x 参考答案 1-5 CDBBC 6-10 CACBD 3 2sin 3A       （9 分） 20 ,3 3 3 3A A         当 3 2A    即 6A  时， 2 42 3 cos sin( )2 3 A B  的最大值为 2 3 ，此时 6B  2 42 3 cos sin( )2 3 A B   的最大值为 2 3 ，取得最大值时， 6A B   （12 分） 17、解：（1） 1 4 4 4 2 4 2 1 24 3 CP A     （4 分） X 的分布列为 X 20 5 10 20 P 3 8 1 3 1 4 1 24 （10 分）    3 1 1 1 3520 5 10 208 3 4 24 6EX             （12 分） 18、解：（1）等边三角形 ABC 的边长为 3，且 AD 1=DB 2 CE EA  ， 1, 2AD AE   在 ADE 中， 60DAE   ，由余弦定理得 3DE  ， 2 2 2AD DE AE   AD DE  ，折叠后有 1A D DE （3 分） 二面角 1A DE B  为直二面角，平面 1A DE  平面 BCED 又平面 1A DE  平面 BCED DE ， 1A D  平面 1A DE ， 1A D DE 1A D  平面 BCED （5 分） （2）假设在线段 BC 上存在点 P ，使得直线 1PA 与平面 1A BD 所成的角为 60 由（1）证明， 可知 DE DB ， 1A D BCED 平面 ，以 D 为坐标原 点，以射线 1, ,DB DE DA 分别为 x 轴， y 轴， z 轴的正半轴，建立空间直角坐标系 D xyz ，如图过点 P 作 PH BD ，垂足为 H ，连接 1 ,A H PH 设  2 0 2 3PB a a   ，则 , 3 , 2BH a PH a DH a         1 0,0,1 , 2 , 3 ,0 , 0, 3,0A P a a E  （7 分）  1 2, 3 ,1PA a a    1ED A BD 平面 ， 1A BD平面 的一个法向量为  0, 3,0DE  （9 分） 1PA 与 1A BD平面 所成的角为 60 1 2 1 3 3sin 60 24 4 5 3 PA DE a PA DE a a             ，解得 5 4a  （11 分） 52 2PB a   ，满足 0 2 3a  ，符合题意 在线段 BC 上存在点 P ，使得直线 1PA 与平面 1A BD 所成的角为 60 ，此时 5 2PB  （12 分） 19、解：（1）设 1 22 ,a k a k  ， 1 2 3, ,a a a 成等差数列， 3 32 2 , 0k a k a     （2 分） ○1 当 k 为偶数时， 2 3 0, 0,2 2 a ka k     此时 1 0a  （4 分） x P B C E D A1 y z H ○1 当 k 为奇数时， 2 3 1 1 0, 1,2 2 a ka k      此时 1 2a  综合上述，可得 1a 的值为 2 或 0 （6 分） （2） 2 11 logn a  ， 2 11 logn a   ， 1 1 2na   （7 分） 又由定义可知， 1 2 1 2 n n n n n a a a a a       为偶数 为奇数 1 2 n n aa   ， 1 1 2 n n a a   （9 分） 11 2 1 11 1 1 2 1 1 1 2 12 2 nn n n n n n n a a aa a aa a a              , 0n na N a   综上可知，当 2 11 log ( )n a n N    时，都有 0na  （12 分） （2）由（1）知椭圆 C 的“准圆”方程为 2 2 5x y  设点  0 0,P x y ，则 2 2 0 0 5x y  （7 分） 设经过点  0 0,P x y 与椭圆C 相切的直线为  0 0y k x x y   联立  0 0 2 2 13 2 y k x x y x y      消去 y ，得     22 2 0 0 0 02 3 6 3 6 0k x k kx y x kx y       由 0  ，化简得   2 2 2 0 0 0 03 2 3 0x k x y k x     （10 分） 设直线 1 2,l l 的斜率分别为 1 2,k k . 直线 1l ， 2l 与椭圆C 相切 1 2,k k 满足方程   2 2 2 0 0 0 03 2 3 0x k x y k x     1 2 1k k    ，故直线 1l 与 2l 垂直 (13 分) 21、解：（1）由题意可知      ( ) ln 0aF x f x g x x xx       ' 2 2 1 a x aF x x x x     （1 分） ○1 当 0a  时，  ' 0F x  在 0, 上恒成立  F x 的增区间为  0, ○2 当 0a  时，令  ' 0F x  得 x a ；令  ' 0F x  得 0 x a   F x 的增区间为 , ,a  减区间为  0,a 综合上述可得：当 0a  ，增区间为 0, ； 当 0a  时，增区间为 , ,a  减区间为 0,a （4 分）  ' 0h x   h x 在  0,2 上是减函数，即  'G x 在 0,2 上是减函数 要证 0 1 2x x x ，只需证    ' ' 0 1 2G x G x x ，即证    ' ' 0 1 2 0G x G x x  对任意  1 2, 0,2x x  ，存在  0 1 2,x x x 使得      2 1' 2 1 G x G xG x x x       2 1 1 2' ' 2 1 0 1 2 2 1 1 2 ln ln 1 ln x x x xx xG x G x x x x x x            2 2 22 1 2 2 1 1 1 11 1 2 2 1 2 1 2 1 11 1 ln 1ln 22 1 x x xxx x x x x x xx x x x x xx x x                     1 20 2x x   2 1 2 1 0, 1xx x x     2 1 1 0x x    只需要证 2 2 2 1 1 1 1 1 ln 1 02 x x x x x x               ，即要证： 2 12 21 1 2 1 ln 1 x xx xx x     