【数学】2018届一轮复习苏教版三角函数线教案

【数学】2018届一轮复习苏教版三角函数线教案

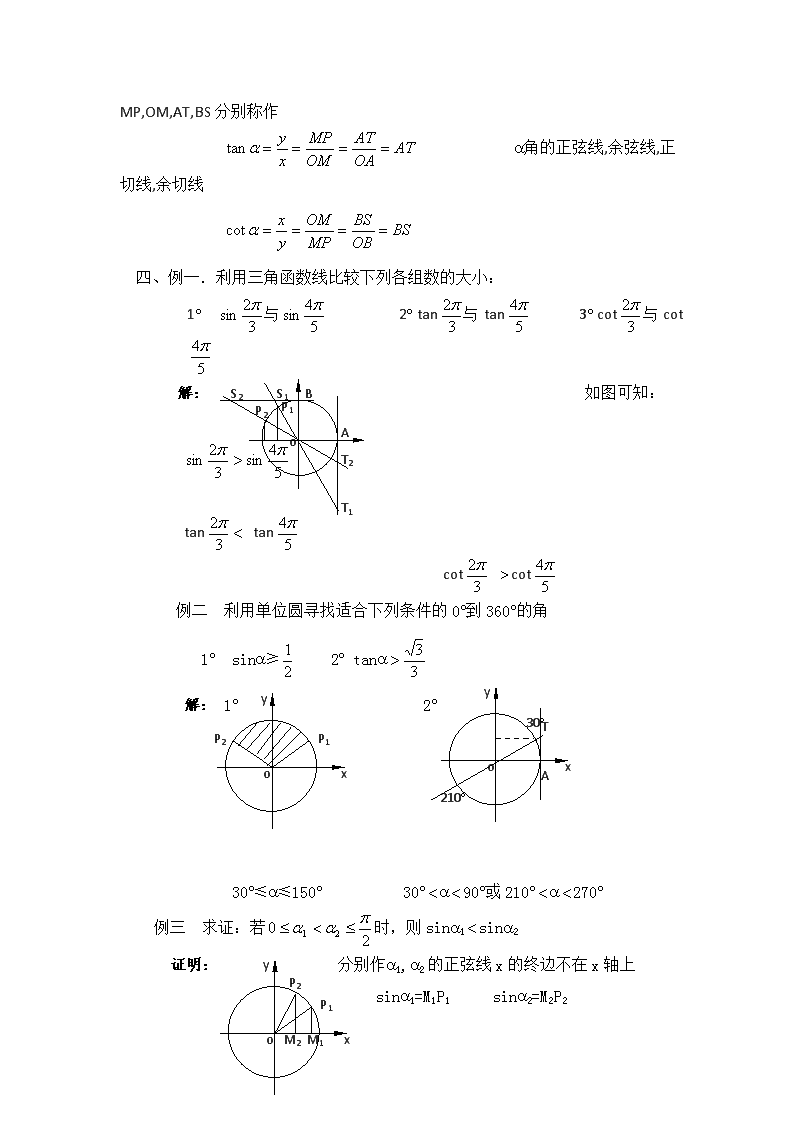
第六教时 教材：三角函数线 目的：要求学生掌握用单位圆中的线段表示三角函数值，从而使学生对三角函数的定义域、值域有更深的理解。‎ 过程：一、复习三角函数的定义，指出：“定义”从代数的角度揭示了三角函数是一个“比值”‎ 二、提出课题：从几何的观点来揭示三角函数的定义：‎ 用单位圆中的线段表示三角函数值 三、新授：‎ 1． 介绍（定义）“单位圆”—圆心在原点O，半径等于单位长度的圆 2． 作图：（课本P14 图4-12 ）‎ 此处略 …… …… ……… …… ……‎ ‎ 设任意角a的顶点在原点，始边与轴的非负半轴重合，角a的终边也与单位圆交于P，坐标轴正半轴分别与单位圆交于A、B两点 ‎ 过P(x,y)作PM^x轴于M，过点A(1,0)作单位圆切线，与a角的终边或其反向延长线交于T，过点B(0,1)作单位圆的切线，与a角的终边或其反向延长线交于S 3． 简单介绍“向量”（带有“方向”的量—用正负号表示）‎ ‎“有向线段”（带有方向的线段）‎ 方向可取与坐标轴方向相同，长度用绝对值表示。‎ 例：有向线段OM，OP 长度分别为 ‎ 当OM=x时 若 OM看作与x轴同向 OM具有正值x ‎ 若 OM看作与x轴反向 OM具有负值x 4． ‎ ‎ 有向线段MP,OM,AT,BS分别称作 ‎ ‎ a角的正弦线,余弦线,正切线,余切线 ‎ ‎ ‎ 四、例一．利用三角函数线比较下列各组数的大小：‎ ‎1° 与 2° tan与tan 3° cot与cot A B o T2‎ T1‎ ‎ S2 S1‎ P2‎ P1‎ ‎ M‎2 M1 S1‎ ‎ 解： 如图可知：‎ ‎ [来源: http://wx.jtyjy.com/]‎ ‎ tan tan ‎ cot cot ‎ 例二 利用单位圆寻找适合下列条件的0°到360°的角 x y o T A ‎210° ‎30° x y o P1‎ P2‎ ‎1° sina≥ 2° tana ‎ 解： 1° 2° ‎ ‎ ‎30°≤a≤150° 30°a90°或210°a270° x y o P1‎ P2‎ M1‎ M2‎ 例三 求证：若时，则sina1sina2‎ 证明： 分别作a1,a2的正弦线x的终边不在x轴上 ‎ sina1=M1P1 sina2=M2P2 ‎ ‎∵‎ ‎∴M1P‎1 M2‎P2 即sina1sina2[来源: http://wx.jtyjy.com/]‎ 五、小结：单位圆，有向线段，三角函数线 http://wx.jtyjy.com/‎ 六、作业： 课本 P15 练习 P20习题4.3 2 ‎ ‎ 补充：解不等式：() [来源:学+科+网Z+X+X+K]‎ ‎ 1°sinx≥ 2° tanx 3°sin2x≤‎