八年级上数学课件八年级上册数学课件《勾股定理的图形验证》 北师大版 (8)_北师大版
1.1 探索勾股定理(2)
——勾股定理的验证及应用
1.1.2 勾股定理的验证及应用
知识回顾:
直角三角形的两直角边的平方和等于斜边的平方.
1.1.2 勾股定理的验证及应用
1.勾股定理
如果用a, b和c分别表示直角三角形的两直角边
和斜边,那么a2+b2=c2
2.填空
(1)在Rt△ABC中, ∠C=900, 若a=5, b=12,则
c = .
(2)在Rt△ABC中, 若a=3, b=5,则c2 = .
13
16或34
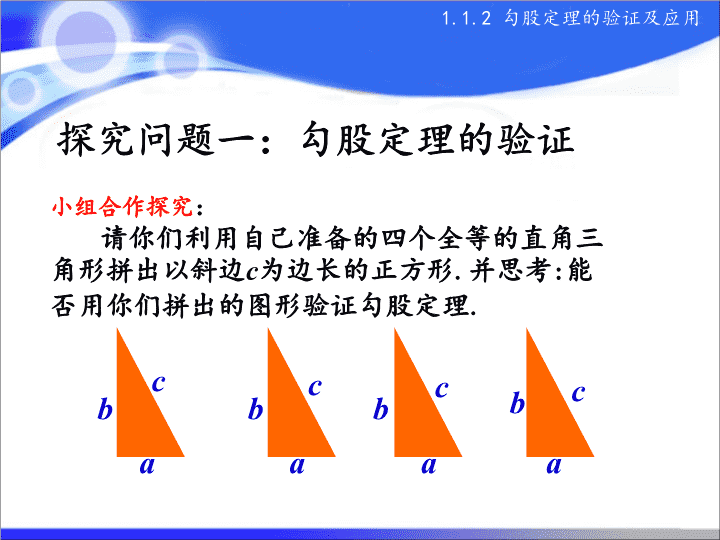
探究问题一:勾股定理的验证
小组合作探究:
请你们利用自己准备的四个全等的直角三
角形拼出以斜边c为边长的正方形.并思考:能
否用你们拼出的图形验证勾股定理.
1.1.2 勾股定理的验证及应用
a
b
c
a
b
c
a
b
c
a
b c
验证方法三:
c
a
bc
a
b
总统证法
2
2
1
)+(=梯形 baS ABCD
22
2
1
)
2
1
cabba +=+(
2
2
1
cabS ABCD +=梯形
1.1.2 勾股定理的验证及应用
∴
∵
222 cba =+∴
A B
C
D
E
拓展延伸:
在钝角三角形中,较
短两边的平方和小于最
长边的平方
1.1.2 勾股定理的验证及应用
a2+b2
c2
在直角三角形中,两
直角边的平方和等于斜
边的平方
a2+b2=c2
在锐角三角形中,较
短两边的平方和大于最
长边的平方
a2+b2=
c2=
a2+b2=
c2=
17
29
13
9
例.我方侦察员小王在距离东西向公路400m处侦
察,发现一辆敌方汽车在公路上疾驶. 他赶紧拿
出红外测距仪,测得汽车与他相距400m,10s后,
汽车与他相距500m,你能帮小王计算敌方汽车的
速度吗?
探究问题二:勾股定理的应用
利用勾股定理解决实际问题
1.1.2 勾股定理的验证及应用
50
0400
C(汽车) B(汽车)
A (小王)
公路
1.《九章算术》中的折竹问题:“今有竹高一丈,
末折抵地,去根六尺,问折高者几何?”
题意是:有一根竹子原高1
丈(1丈=10尺),中部有一
处折断,竹梢触地面处离竹
根6尺,试问折断处离地面
多高?
A
B C
6
巩固练习:
1.1.2 勾股定理的验证及应用
收获与体会:你在本节课都有哪些收获呢?
1.1.2 勾股定理的验证及应用
1.勾股定理的验证
毕达哥拉斯证法
赵爽弦图证法
总统证法
3.勾股定理的实际应用
⑴画图定直角三角形
⑵利用勾股定理求解
⑶作答
2.三角形的三边关系
钝角三角形:a2+b2c2
思考题:中考链接之折叠问题
1.1.2 勾股定理的验证及应用
如图所示,一张直角三角形纸片,两直角边AC=
6 cm,BC=8 cm,现将直角边AC沿AD折叠,使
点C落在斜边AB上的点E处,试求CD的长.
法二:面积法
法一:利用勾股定理列方程
S△ABC= S△ACD+ S△ABD
10
6
8
6
4
x 8-x
x
作业:
1.随堂练习,习题1.2:第1题,(选做第3题)
2.课后达标检测(注意把握时间)
3.上网或查阅有关书籍,搜集至少1种勾股定
理的其它证法,至少1个勾股定理的应用问题
1.1.2 勾股定理的验证及应用
课后达标测评(满分60分):
一、判断题(每空5分):
1.△ABC的两边AB=5,AC=12,则BC=13 ( )
2.△ABC的a=6,b=8,则c=10 ( )
二、填空题(每空5分)
1.在△ABC中, ∠C=90°,
(1)若c=10,a:b=3:4,则a=____,b=__ _.
(2)若a=7,b=24,则c=______.
2.在△ABC中, ∠C=90°,若AC=6,CB=8,则△ABC面积为
_____,斜边为上的高为______.
1.1.2 勾股定理的验证及应用
课后达标测评(满分60分):
三、计算题
1.(10分)飞机在空中水平飞行,某一时刻刚好飞到一
个男孩头顶正上方4000 米处,过了 20 秒,飞机距离这个
男孩头顶5000米,飞机每时飞行多少千米?
2.(15分)如图,将边长为8cm的正方形ABCD折叠,使
点D落BC边的中点E处,点A落在F处,折痕为MN,求线段CN
长
1.1.2 勾股定理的验证及应用