- 2021-05-19 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上数学课件八年级上册数学课件《勾股定理的应用》 北师大版 (5)_北师大版
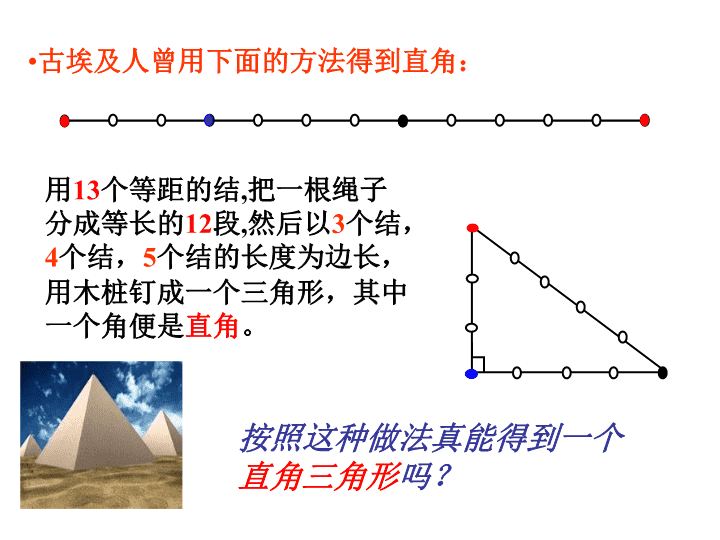
1.直角三角形有哪些性质? 2.如何判断三角形是直角三角形? 按照这种做法真能得到一个 直角三角形吗? •古埃及人曾用下面的方法得到直角: 用13个等距的结,把一根绳子 分成等长的12段,然后以3个结, 4个结,5个结的长度为边长, 用木桩钉成一个三角形,其中 一个角便是直角。 3 4 5 请同学们观察,这个三角形的三条边有什么关系吗? 3 2 4 2 5 2+ = 3 4 5 A C B A′ B′C′ 3 4 古埃及人的做法: △ABC中, BC=3、 AC=4、AB=5 这两个三角形有什么关系? 我们作RT △ABC,使 =3、 =4B′C′ A′C′ ∵ ∠ C’=900 ∴ A’B’2= a2+b2 ∵ a2+b2=c2 ∴ A’B’ 2=c2 ∴ A’B’ =c ∵ 边长取正值 ∴ △ ABC ≌ △ A’B’C’(SSS) ∴ ∠ C= ∠ C’=90° BC=a=B’C’ CA=b=C’A’ AB=c=A’B’ 已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2 求证:△ ABC是直角三角形 证明:画一个△A’B’C’,使∠ C’=90°,B’C’=a, C’A’=b 在△ ABC和△ A’B’C’中 则 △ ABC是直角三角形 (直角三角形的定义) 勾股定理的逆命题 A C B A′ B′C′ a b 证明: a b c 勾股定理的逆命题 如果直角三角形两直角边分别为a,b, 斜边为c,那么 a2 + b2 = c2 勾股定理 如果三角形的三边长a、b、c满足 那么这个三角形是直角三角形。且边 C所对的角为直角。 a2 + b2 = c2 互逆命题 定理 定理 例1 判断由a、b、c组成的三角形是不是直角三角形: (1) a=15 , b =8 , c=17 例题解析 (2) a=13 , b =15 , c=14 例 2.在△ABC中,a=15, b=17, c=8,求 此三角形的面积。 8 15 17 AB C 下面以a,b,c为边长的三角形是不是直 角三角形?如果是那么哪一个角是直角? (1) a=25 b=20 c=15 ____ _____ ; (2) a=13 b=14 c=15 ____ _____ ; (4) a:b: c=3:4:5 _____ _____ ; 是 是 不是 是 ∠ A=900 ∠ B=900 ∠ C=900 (3) a=1 b=2 c= ____ _____ ;3 像25,20,15,能够成为直角三角形 三条边长的三个正整数,称为勾股数. 13 A B C D A B C D 3 4 5 12 例 3 一个零件的形状如左图所示,按规定这个零 件中∠A和∠DBC都应为直角。工人师傅量得这 个零件各边尺寸如右图所示,这个 零件符合要求 吗? 例题解析 • 例4: “远航”号、“海天”号轮船 同时离开港口,各自沿一固定方向航 行,“远航”号每小时航行16海里, “海天”号每小时航行12海里。它们 离开港口一个半小时后相距30海里。 如果知道“远航”号沿东北方向航行, 能知道“海天”号沿哪个方向航行吗? P E Q R N 远航海天 B ) (,2)( 22 则此三角形是 满足条件、、三角形三边长 abcba cba A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形 1. 已知:如图,四边形ABCD 中,∠B=900,AB=3,BC=4, C D= 1 2, A D= 1 3 ,求四边形 ABCD的面积? A B C D S四边形ABCD=36 吗?说明理由△ABC是直角三角形 n是正整数),m,n,>(m 且 cb,a, 分别为△ABC三角形的三边 1、已知 nm=c2mn,=b,n-m =a 2222 1、 已知a,b,c为△ABC的三边,且 满足 a2+b2+c2+338=10a+24b+26c. 试判断△ABC的形状. 2、△ABC三边a,b,c为边向外作 正方形,正三角形,以三边为 直径作半圆,若S1+S2=S3成立, 则 是直角三角形吗? A C ab c S1S2 S3 BA B C ab c S1 S2 S3查看更多