八年级上数学课件《平面直角坐标系》 (19)_苏科版

八年级上数学课件《平面直角坐标系》 (19)_苏科版

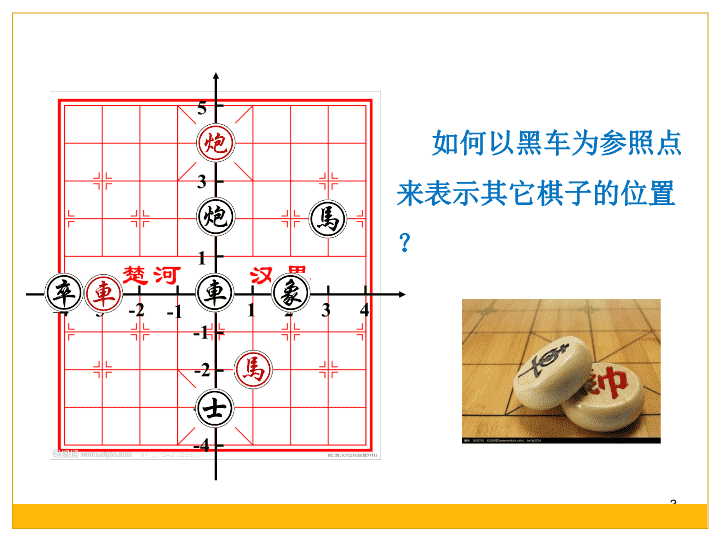
5.2 平面直角坐标系 2 相传韩信发明了中国象棋！ 3 5 -4 4 3 2 1 -3 -2 -1 -4 -3 -2 1 2 3 4-1 如何以黑车为参照点 来表示其它棋子的位置？ 4 y x 5 -4 4 3 2 1 -3 -2 -1 -4 -3 -2 1 2 3 4-1 O 平面内，两条互相垂 直的数轴构成平面直角坐 标系 简称为直角坐标系. 平面直角坐标系 x轴（横轴） y轴（纵轴） 坐 标 轴 两轴的交点O叫原点 y x 5 -4 4 3 2 1 -3 -2 -1 -4 -3 -2 1 2 3 4-1 O 平面直角坐标系 坐标轴不属 于任何象限 第四象限 第一象限第二象限 第三象限 两条坐标轴将平面分 成的4个区域称为象限 平面直角坐标系 直角坐标系的创立，为用代数方法研究 几何问题开辟了一条崭新的道路，引起 了数学的深刻革命。为了纪念笛卡儿， 直角坐标系也叫笛卡尔坐标系。 平面直角坐标系(特征） （1）两条数轴互相垂直且原点重 合； （2）通常取向右、向上为正方向； （3）两条数轴的单位长度一般取 相同. y x 5 -4 4 3 2 1 -3 -2 -1 -4 -3 -2 1 2 3 4-1 O x-1 O 1 2 3 4 5-4 -3 -2 -1 x 3 1 4 2 5 -2 -4 -3 y B A 在直角坐标系中，指出下列各点的位置。 A（3，2）， B(2,3) 问题1：如果任意给出一个有序 实数对， 那么在平面直角坐标系内， 是否存在与它对应的一个点呢？ x-1 O 1 2 3 4 5-4 -3 -2 -1 x 3 1 4 2 5 -2 -4 -3 y C D •问题2：如图，如果P是平面直角坐标系中任一 点，是否存在对应的一对有序实数呢？ 3 2 1 -3 -2 -1 -4 -5 4 5 x1-1-2-3-4 2-5 3o 54 P 这样的有序实数对叫 做点的坐标。其中， a称为p的横坐标，b 称为p的纵坐标记作： p（a,b） a b （a，b） y x 5 -4 4 3 2 1 -3 -2 -1 -4 -3 -2 1 2 3 4-1 O 例题：分别写出图中E,F及原点O的坐标。并在直角坐 标系中画出下列各点： G(0，-2) , H(-2，-1.5) E F   o 1 2 3 4 5-4 -3 -2 -1 x 3 1 4 2 5 -2 -4 -1 -3 y 第二象限 第一象限 第三象限 第四象限 x轴上的点：纵坐标是0。 y轴上的点：横坐标是0。 (+,+)(-,+) (+,-)(-,-) 写出你的坐标 0 口令： 1.（0，-2） 3.纵坐标为0 4.横、纵坐标都为0 2.（-2，3） 5.横、纵坐标 互为相反数 6.横、纵坐 标绝对值为 2，且在第 三象限 （一）仔细辨一辨： 1、（2，3）和（3，2）表示同一个点.（ ） 2、在直角坐标系内，原点的坐标是0.（ ） 3、第一象限内的点的横坐标和纵坐标均为正数.（ ）　 4、坐标轴上的点的横坐标与纵坐标至少有一个为0.（ ） √ √ × × （二）精心选一选： 1、点（-1，2）在（ ） A、第一象限；B、第二象限；C、第三象限；D、第四象限 2、若点（x，y）在第三象限内，则（ ） A、x>0，y>0； B、x>0，y<0 ； C、x<0，y<0 ； D、x<0，y>0． B C 3、若点P（x，y）在第四象限，|x|=2,|y|=3，则P点的坐 标为( ) A、(2,3)； B、(2,-3)； C、(-2,3)； D、(-2,-3) B 5 1 (三）认真填一填： 已知P点坐标为（a-1，a-5） ①如果点P在x轴上，则a= ； ②如果点P在y轴上，则a= ； ③若a=-3 ，则P在第 象限内； ④若a=3，则点P在第 象限内. 三 四 今天你有哪些收获？ 课堂小结： 1、平面直角坐标系相关概念。 2、在平面直角坐标系中，由点求坐标，根据坐 标找出点。 同一直角坐标系中的点 有序实数对（坐标） 一一对应 “形” “数” 3、各个象限中的点、x轴及y轴上点的坐标的特征： 第一象限：（＋，＋）第二象限：（－，＋） 第三象限：（－，－）第四象限：（＋，－） x轴上的点的纵坐标为0，表示为（x，0） y轴上的点的横坐标为0，表示为（0，y） 21 （1）课本 P122 练习1、2； 作业布置： （2）补充练习. 阅读与欣赏——笛卡儿的梦 笛卡儿（1596—1650年）法国著名的数学家，青年时期曾参加军队到荷兰。 1619年的冬天，莱茵河畔乌儿小镇的军用帐篷中。入夜， 万簌俱静，笛卡儿彻 夜不眠，沉迷在深思之中，他望着天空，想着怎么用几个数字来表示星星的位 置呢？自己随军奔波，给家里去信怎么报告自己的位置呢？他完全进入数学的 世界，继续进行着数与形的冥想…… 他仿佛到了无人的旷野，他的排长站在他的面前说：“你不是想用数学来解 释自然界吗？”排长说着抽出了两支箭，拿在手里搭成一个十字架，箭头一个 向上，一个朝右。他将十字架举过头说：“你看，假如我们把天空的一部分看 成是一个平面，这个天空就被分成四个部分。这两支箭能射向无限远，天上随 便那颗星星，你只要向这两支箭上分别引垂线段，就会得到两个数字，这星的 位置就一清二楚了。”笛卡儿还不清楚又问道“负数又该怎样表示呢？”排长 笑道：“两支箭的十字交叉处定为零，向上向右为正数，向下向左不就是负数 了吗？”笛卡儿高兴地扑了过去，却扑通一声跌入河中……正在大喊，却被人 叫醒 ，天已大亮了。笛卡儿发疯似地拿出本子和铅笔，把梦中见到的全都画了 出来。后人传说笛卡儿创立的直角坐标系就是这样从梦中得来的。 直角坐标系的创立，为用代数方法研究几何问题开辟了一条崭新的道路，引 起了数学的深刻革命。为了纪念笛卡儿，直角坐标系也叫笛卡儿坐标系。 谢谢大家，下次再见！ Tel ： 15995312812 E-mail ： 864881744@qq.com