2020全国中考数学试卷分类汇编(2)专题35 尺规作图

2020全国中考数学试卷分类汇编(2)专题35 尺规作图

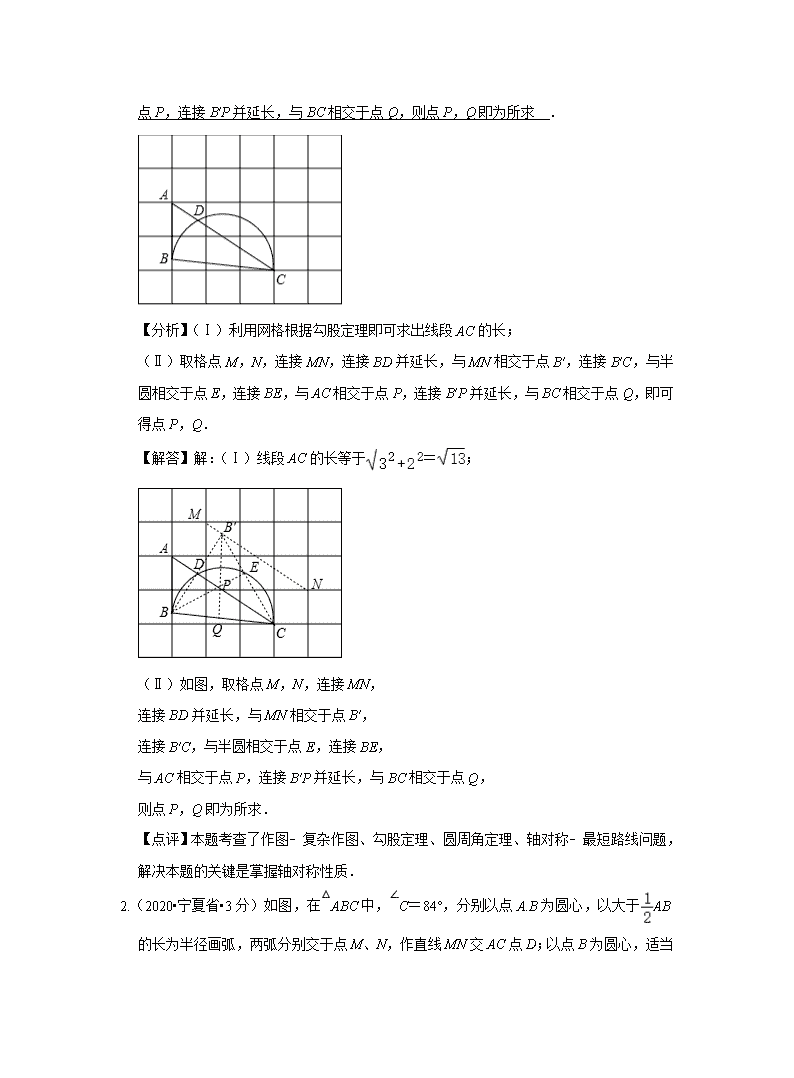
尺规作图 ‎ 一.选择题 ‎1. （2020•四川省成都市•3分）如图，在中，按以下步骤作图：①分别以点和为圆心，以大于的长为半径作弧，两弧相交于点和；②作直线交于点，连接．若，，则的长为（ ）‎ A. 2 B. 3 C. 4 D. 6‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由作图可知， M N是线段BC的垂直平分线，据此可得解．‎ ‎【详解】解：由作图可知， M N是线段BC的垂直平分线，‎ ‎∴BD=CD=AC-AD=6-2=4，‎ 故选：C ‎【点睛】本题考查了线段垂直平分线的性质，灵活的利用线段垂直平分线上的点到线段两端的距离相等这一性质添加辅助线是解题的关键．‎ 二.填空题 ‎1. （2020·天津市·3分）如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，C均落在格点上，点B在网格线上，且AB＝．‎ ‎（Ⅰ）线段AC的长等于　　．‎ ‎（Ⅱ）以BC为直径的半圆与边AC相交于点D，若P，Q分别为边AC，BC上的动点，当BP+PQ取得最小值时，请用无刻度的直尺，在如图所示的网格中，画出点P，Q，并简要说明点P，Q的位置是如何找到的（不要求证明）　取格点M，N，连接MN，连接BD并延长，与MN相交于点B′，连接B′C，与半圆相交于点E，连接BE，与AC 相交于点P，连接B′P并延长，与BC相交于点Q，则点P，Q即为所求　．‎ ‎【分析】（Ⅰ）利用网格根据勾股定理即可求出线段AC的长；‎ ‎（Ⅱ）取格点M，N，连接MN，连接BD并延长，与MN相交于点B′，连接B′C，与半圆相交于点E，连接BE，与AC相交于点P，连接B′P并延长，与BC相交于点Q，即可得点P，Q．‎ ‎【解答】解：（Ⅰ）线段AC的长等于＝；‎ ‎（Ⅱ）如图，取格点M，N，连接MN，‎ 连接BD并延长，与MN相交于点B′，‎ 连接B′C，与半圆相交于点E，连接BE，‎ 与AC相交于点P，连接B′P并延长，与BC相交于点Q，‎ 则点P，Q即为所求．‎ ‎【点评】本题考查了作图﹣复杂作图、勾股定理、圆周角定理、轴对称﹣最短路线问题，解决本题的关键是掌握轴对称性质．‎ ‎2.（2020•宁夏省•3分）如图，在△ABC中，∠C＝84°，分别以点A.B为圆心，以大于AB的长为半径画弧，两弧分别交于点M、N，作直线MN交AC点D；以点B 为圆心，适当长为半径画弧，分别交BA.BC于点E.F，再分别以点E.F为圆心，大于EF的长为半径画弧，两弧交于点P，作射线BP，此时射线BP恰好经过点D，则∠A＝　32　度．‎ ‎【分析】由作图可得MN是线段AB的垂直平分线，BD是∠ABC的平分线，根据它们的性质可得∠A＝∠ABD＝∠CBD，再根据三角形内角和定理即可得解．‎ ‎【解答】解：由作图可得，MN是线段AB的垂直平分线，BD是∠ABC的平分线，‎ ‎∴AD＝BD，，‎ ‎∴∠A＝∠ABD，‎ ‎∴∠A＝∠ABD＝∠CBD，‎ ‎∵∠A+∠ABC+∠C＝180°，且∠C＝84°，‎ ‎∴∠A+2∠ABD＝180°﹣∠C，‎ 即3∠A＝180°﹣84°，‎ ‎∴∠A＝32°．‎ 故答案为：32．‎ ‎【点评】本题考查了作图﹣复杂作图，解决本题的关键是掌握线段垂直平分线的作法和角平分线的作法．‎ ‎3.（2020•辽宁省本溪市•3分）如图，在Rt△ABC中，∠ACB＝90°，AC＝2BC，分别以点A和B为圆心，以大于AB的长为半径作弧，两弧相交于点M和N，作直线MN，交AC于点E，连接BE，若CE＝3，则BE的长为　5　．‎ ‎【分析】设BE＝AE＝x，在Rt△BEC中，利用勾股定理构建方程即可解决问题．‎ ‎【解答】解：由作图可知，MN垂直平分线段AB，‎ ‎∴AE＝EB，‎ 设AE＝EB＝x，‎ ‎∵EC＝3，AC＝2BC，‎ ‎∴BC＝（x+3），‎ 在Rt△BCE中，∵BE2＝BC2+EC2，‎ ‎∴x2＝32+[（x+3）]2，‎ 解得，x＝5或﹣3（舍弃），‎ ‎∴BE＝5，‎ 故答案为5．‎ ‎【点评】本题考查作图﹣基本作图，线段的垂直平分线的性质，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．‎ ‎4. (2020•山东省潍坊市•3分)如图，在Rt△ABC中，∠C＝90°，∠B＝20°，PQ垂直平分AB，垂足为Q，交BC于点P．按以下步骤作图：①以点A为圆心，以适当的长为半径作弧，分别交边AC，AB于点D，E；②分别以点D，E为圆心，以大于DE的长为半径作弧，两弧相交于点F；③作射线AF．若AF与PQ的夹角为α，则α＝　 　°．‎ ‎【分析】根据直角三角形两锐角互余得∠BAC＝70°，由角平分线的定义得∠2＝35°，由线段垂直平分线可得△AQM是直角三角形，故可得∠1+∠2＝90°，从而可得∠1＝55°，最后根据对顶角相等求出α．‎ ‎【解答】解：如图，‎ ‎∵△ABC是直角三角形，∠C＝90°，∴∠B+∠BAC＝90°，‎ ‎∵∠B＝20°，∴∠BAC＝90°－∠B＝90°－20°＝70°，‎ ‎∵AM是∠BAC的平分线，∴，‎ ‎∵PQ是AB的垂直平分线，∴△AMQ是直角三角形，∴∠AMQ+∠2＝90°，‎ ‎∴∠AMQ＝90°－∠2＝90°－35°＝55°，‎ ‎∵∠α与∠AMQ是对顶角，∴∠α＝∠AMQ＝55°．故答案为55°．‎ ‎【点评】此题考查了直角三角形两锐角互余，角平分线的定义，线段垂直平分线的性质，对顶角相等等知识，熟练掌握相关定义和性质是解题的关键．‎ 三.解答题 ‎1. (2020•山东省青岛市•4分)已知：△ABC．‎ 求作：⊙O，使它经过点B和点C，并且圆心O在∠A的平分线上．‎ ‎【分析】作出∠A的平分线和线段BC的垂直平分线，找到它们的交点，即为圆心O，再以OB为半径画出⊙O，得出答案．‎ ‎【解答】解：如图所示：⊙O即为所求．‎ ‎【点评】此题主要考查了复杂作图，正确掌握角平分线和垂直平分线的作法是解题关键．‎ ‎2. 2020年青海省.如图，中，．‎ ‎（1）尺规作图：作的外接圆；作的角平分线交于点D，连接AD．（不写作法，保留作图痕迹）‎ ‎（2）若AC =6，BC =8，求AD的长．‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据外接圆，角平分线的作法作图即可；‎ ‎（2）连接AD，OD，根据CD平分，得°，根据圆周角与圆心角的关系得到°，在中计算AB，在中，计算AD．‎ ‎【详解】（1）作图如下：‎ ‎（2）连接AD，OD，如图所示 由（1）知：平分，且°‎ ‎∴°‎ ‎∴°‎ 在中，，‎ ‎∴，即 在中，‎ ‎【点睛】本题考查了三角形的外接圆，角平分线，以及利用圆周角与圆心角的关系，及勾股定理计算线段长度的方法，熟知以上方法是解题的关键．‎ ‎3. （2020•四川省达州市•7分）如图，点O在∠ABC的边BC上，以OB为半径作⊙O，∠ABC的平分线BM交⊙O于点D，过点D作DE⊥BA于点E．‎ ‎（1）尺规作图（不写作法，保留作图痕迹），补全图形；‎ ‎（2）判断⊙O与DE交点的个数，并说明理由．‎ ‎【分析】（1）根据要求，利用尺规作出图形即可．‎ ‎（2）证明直线AE是⊙O的切线即可解决问题．‎ 解：（1）如图，⊙O，射线BM，直线DE即为所求．‎ ‎（2）直线DE与⊙O相切，交点只有一个．‎ 理由：∵OB＝OD，‎ ‎∴∠ODB＝∠OBD，‎ ‎∵BD平分∠ABC，‎ ‎∴∠ABM＝∠CBM，‎ ‎∴∠ODB＝∠ABD，‎ ‎∴OD∥AB，‎ ‎∵DE⊥AB，‎ ‎∴AE⊥OD，‎ ‎∴直线AE是⊙O的切线，‎ ‎∴⊙O与直线AE只有一个交点．‎ ‎4. （2020•陕西•5分）如图，已知△ABC，AC＞AB，∠C＝45°．请用尺规作图法，在AC边上求作一点P，使∠PBC＝45°．（保留作图痕迹．不写作法）‎ ‎【分析】根据尺规作图法，作一个角等于已知角，在AC边上求作一点P，使∠PBC＝45°即可．‎ ‎【解答】解：如图，点P即为所求．‎ ‎【点评】本题考查了作图﹣基本作图，解决本题的关键是掌握基本作图方法．‎ ‎5. （2020•福建省•10分）如图，C为线段AB外一点．‎ ‎（1）求作四边形ABCD，使得CD∥AB，且CD＝2AB；（要求：尺规作图，不写作法，保留作图痕迹）‎ ‎（2）在（1）的四边形ABCD中，AC，BD相交于点P，AB，CD的中点分别为M，N，求证：M，P，N三点在同一条直线上．‎ ‎【分析】（1）利用尺规作图作CD∥AB，且CD＝2AB，即可作出四边形ABCD；‎ ‎（2）在（1）的四边形ABCD中，根据相似三角形的判定与性质即可证明M，P，N三点在同一条直线上．‎ ‎【解答】解：（1）如图，四边形ABCD即为所求；‎ ‎（2）如图，‎ ‎∵CD∥AB，‎ ‎∴∠ABP＝∠CDP，∠BAP＝∠DCP，‎ ‎∴△ABP∽△CDP，‎ ‎∴＝，‎ ‎∵AB，CD的中点分别为M，N，‎ ‎∴AB＝2AM，CD＝2CN，‎ ‎∴＝，‎ 连接MP，NP，‎ ‎∵∠BAP＝∠DCP，‎ ‎∴△APM∽△CPN，‎ ‎∴∠APM＝∠CPN，‎ ‎∵点P在AC上，‎ ‎∴∠APM+∠CPM＝180°，‎ ‎∴∠CPN+∠CPM＝180°，‎ ‎∴M，P，N三点在同一条直线上．‎ ‎【点评】本题考查了作图﹣复杂作图、相似三角形的判定与性质，解决本题的关键是掌握相似三角形的判定与性质．‎ ‎6.（2020•北京市•5分）已知：如图，△ABC为锐角三角形，AB＝AC，CD∥AB．‎ 求作：线段BP，使得点P在直线CD上，且∠ABP＝∠BAC．‎ 作法：①以点A为圆心，AC长为半径画圆，交直线CD于C，P两点；‎ ‎②连接BP．‎ 线段BP就是所求作的线段．‎ ‎（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；‎ ‎（2）完成下面的证明．‎ 证明：∵CD∥AB，‎ ‎∴∠ABP＝　∠BPC　．‎ ‎∵AB＝AC，‎ ‎∴点B在⊙A上．‎ 又∵点C，P都在⊙A上，‎ ‎∴∠BPC＝∠BAC（　同弧所对的圆周角等于圆心角的一半　）（填推理的依据）．‎ ‎∴∠ABP＝∠BAC．‎ ‎【分析】（1）根据作法即可补全图形；‎ ‎（2）根据等腰三角形的性质和同弧所对圆周角等于圆心角的一半即可完成下面的证明．‎ ‎【解答】解：（1）如图，即为补全的图形；‎ ‎（2）证明：∵CD∥AB，‎ ‎∴∠ABP＝∠BPC．‎ ‎∵AB＝AC，‎ ‎∴点B在⊙A上．‎ 又∵点C，P都在⊙A上，‎ ‎∴∠BPC＝∠BAC（同弧所对的圆周角等于圆心角的一半），‎ ‎∴∠ABP＝∠BAC．‎ 故答案为：∠BPC，同弧所对的圆周角等于圆心角的一半．‎ ‎【点评】本题考查了作图﹣复杂作图、等腰三角形的性质、圆周角定理，解决本题的关键是综合运用以上知识．‎ ‎7.（2020•江西省•6分）如图，在正方形网格中，的顶点在格点上，请仅用无刻度直尺完成以下作图（保留作图痕迹）.‎ ‎（1）在图1中，作关于点对称的；‎ ‎（2）在图2中，作绕点顺时针旋转一定角度后，顶点仍在格点上的.‎ ‎【解析】作图如下：‎