2018-2019学年湖北省宜昌市第二中学高一下学期3月月考数学试卷

2018-2019学年湖北省宜昌市第二中学高一下学期3月月考数学试卷

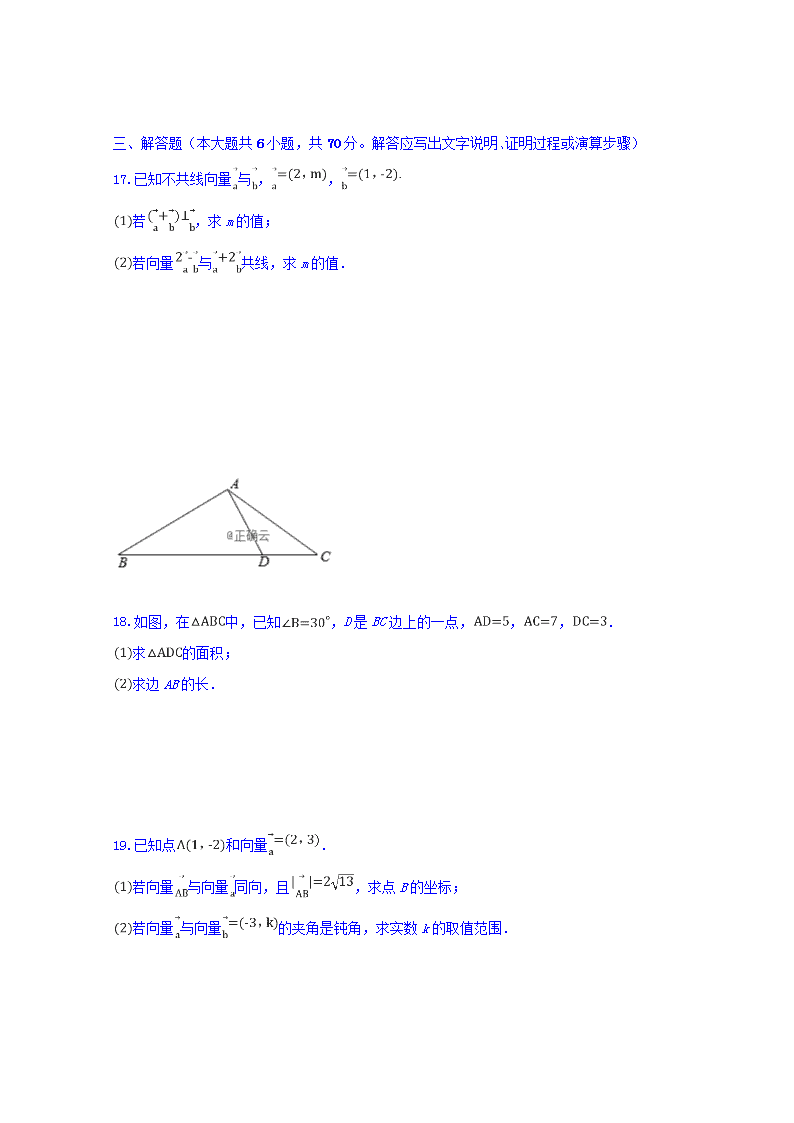
湖北省宜昌市第二中学2018-2019学年高一下学期3月月考数学试卷 一、选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ 1. 在中，D为BC边的中点，若，，则为　　‎ A. B. C. D. ‎ 2. 在中，角A，B，C的对边分别为a，b，，，，则　　‎ A. B. C. D. ‎ 3. 设非零向量，满足则   ‎ A. B. C. D. ‎ 4. 在中，角A，B，C的对边分别为a，b，若，则角A的值为　　‎ A.或 B. 或 C. D. ‎ 5. 已知，，则向量在方向上的投影为　　‎ A. B. C. 2 D. 4‎ 6. ABC中，D为边BC上一点，且满足，则等于　　‎ A. B. C. D. ‎ 7. 的内角A，B，C的对边分别为a，b，若，，，则a等于　　‎ A. 3 B. C. D. 1‎ 8. 设，是平面上的两个单位向量，若，则的最小值是　　‎ A. B. C. D. ‎ 1. 已知，与的夹角为，则    ‎ A. 2 B. 3 C. 4 D. 5‎ 2. 若O为所在平面内任一点，且满足，则的形状为　　‎ A. 等腰三角形 B. 直角三角形 C. 正三角形 D. 等腰直角三角形 3. 如图，在平行四边形ABCD中，M、N分别为AB、AD上的点，且，，连接AC、MN交于P点，若，则的值为　　‎ A. B. ‎ C. D. ‎ 4. 中，角A，B，C的对边分别为a，b，，若，则　‎ A. B. C. D. ‎ 二、填空题（本大题共4小题，每小题5分共20分。把答案填在答题卡的横线上）‎ 5. 化简               ． ‎ ‎14.已知向量与的夹角为，且，那么的值为______．‎ ‎15.设，是两个不共线的向量，，，，若A，B，D三点共线，则实数k的值为______．‎ ‎16.在中，角A，B，C的对边分别为a，b，且，则角C的大小为______ ．‎ 三、解答题（本大题共6小题，共70分。解答应写出文字说明､证明过程或演算步骤）‎ ‎17.已知不共线向量与，，‎ 若，求m的值；‎ 若向量与共线，求m的值．‎ ‎18.如图，在中，已知，D是BC边上的一点，，，．‎ 求的面积；‎ 求边AB的长．‎ ‎19.已知点和向量．‎ 若向量与向量同向，且，求点B的坐标；‎ 若向量与向量的夹角是钝角，求实数k的取值范围．‎ ‎20. 如图，A、B是海面上位于东西方向相距海里的两个观测点，现位于A点北偏东且位于B点北偏西的D点有一艘轮船发出求救信号，位于B点南偏西且与B点相距海里的C点的救援船收到信号后立即前往营救，其航行速度为30海里小时，‎ 试求：轮船D与观测点B的距离BD；‎ 救援船从C处出发沿直线CD航行到达D点所需要的时间．‎ ‎21.如图，边长为2的菱形ABCD中，，E、F分别是BC、DC的中点，G为 BF、DE的交点，若，．‎ 试用，表示；‎ 求的值．‎ ‎22.在锐角中，角A，B，C的对边分别为a，b，c，且满足．‎ 求角C的大小；‎ 若，求ab的取值范围．‎ 数学答案 一、选择题（本大题共12小题，共60.0分）‎ 1. 在中，D为BC的中点，若，，则为　　‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】为BC的中点，，，‎ ‎，‎ 故选：D．‎ 根据向量加减的几何意义即可求出．‎ 本题考查了向量的加减的几何意义，属于基础题．‎ 2. 在中，角A，B，C的对边分别为a，b，，，，则　　‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】【分析】本题考查正弦定理的应用，属于基础题，直接利用正弦定理化简求解即可．‎ ‎【解答】在中，，，，则．‎ 故选C．‎ 3. 设非零向量，满足，则  ‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】【分析】‎ 本题考查两个向量的关系的判断，考查向量的模、向量垂直等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是基础题由题意，推导出，由此得到．‎ ‎【解答】‎ 解：设非零向量满足，‎ ‎，‎ ‎，‎ ‎，，‎ ‎．‎ 故选：A．‎ 1. 在中，角A，B，C的对边分别为a，b，若，则角A的值为　　‎ A.或 B. 或 C. D. ‎ ‎【答案】B ‎【解析】解：，，，‎ 由正弦定理得：，‎ ‎，，即，‎ 或．‎ 故选B 由B的度数求出的值，再由a与b的值，利用正弦定理求出的值，根据a大于b，得到A大于B，利用特殊角的三角函数值即可求出A的度数．‎ 此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．‎ 2. 已知，，则向量在方向上的投影为　　‎ A. B. C. 2 D. 4‎ ‎【答案】A ‎【解析】解：，，即．‎ 故向量在方向上的投影为，‎ 故选：A．‎ 利用向量在方向上的投影为求解．‎ 本题考查了向量的投影的计算，属于基础题．‎ 1. 三角形ABC中，D为边BC上一点，且满足，则等于　　‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】【分析】‎ 本题考查向量的加减混合运算，属基础题．‎ 由，可得，代入已知向量可得．‎ ‎【解答】‎ 解：，‎ ‎，‎ 故选C．‎ 2. 的内角A，B，C的对边分别为a，b，若，，，则a等于　　‎ A. 3 B. C. D. 1‎ ‎【答案】D ‎【解析】解：，，，‎ 由，可得：，整理可得：，‎ 解得：或舍去．‎ 故选：D．‎ 由已知利用余弦定理即可计算得解．‎ 本题主要考查了余弦定理在解三角形中的应用，属于基础题．‎ 1. 设，是平面上的两个单位向量，若，则的最小值是　　‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】解：设，是平面上的两个单位向量，‎ 则，，‎ ‎，‎ ‎，‎ 当时，有最小值，‎ 的最小值是，‎ 故选：C．‎ 根据向量的数量积的运算法则和二次函数的性质即可求出即可．‎ 本题考查了向量的数量积的运算和二次函数的性质，属于基础题．‎ 2. 已知，与的夹角为，则    ‎ A. 2 B. 3 C. 4 D. 5‎ ‎【答案】B ‎【解析】【分析】‎ 首先利用已知条件求出，再根据与的夹角为，列出方程，便可求出的值．‎ ‎【解答】‎ 解：，‎ 与的夹角为，‎ ‎，‎ 解得．‎ 故选B．‎ 1. 若O为所在平面内任一点，且满足，则的形状为　　‎ A. 等腰三角形 B. 直角三角形 C. 正三角形 D. 等腰直角三角形 ‎【答案】A ‎【解析】【分析】‎ 本题考查了平面向量的线性表示与数量积运算问题，是综合性题目根据平面向量的线性表示与数量积运算，结合题意可得出是等腰三角形．‎ ‎【解答】‎ 解：因为，‎ 即；‎ 又因为，‎ 所以，‎ 即，‎ 所以是等腰三角形．‎ 故选A．‎ 2. 如图，在平行四边形ABCD中，M、N分别为AB、AD上的点，且，，连接AC、MN交于P点，若，则的值为　　‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】【分析】‎ 本题考查了平面向量的线性运算，及三点共线的充要条件，属于中档题．‎ 根据向量的加减的几何意义和三点共线即可求出答案．‎ ‎【解答】‎ 解：，，‎ ‎，‎ 三点M，N，P共线．‎ ‎，‎ ‎，‎ 故选C．‎ 1. 中，角A，B，C的对边分别为a，b，，若，则　‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】解：‎ ‎，不共线 即 则 故选B 由已知及向量减法的平行四边形法则可得即，根据向量的基本定理可得a，b，c之间的关系，然后利用余弦定理即可求 本题主要考查了向量减法的四边形法则，平面向量的基本定理及余弦定理的综合应用，解题的关键是把已知变形为 二、填空题（本大题共4小题，共20.0分）‎ 2. 化简               ．‎ ‎【答案】‎ ‎【解析】【分析】‎ 本题主要考查了平面向量的加减运算，按照向量的运算法则运算即可．‎ ‎【解答】‎ 解：，‎ 故答案为．‎ 1. 已知向量与的夹角为，且，那么的值为______．‎ ‎【答案】0‎ ‎【解析】解：由题意知．‎ 故答案为0．‎ 由向量数量积公式进行计算即可．‎ 本题考查向量数量积运算公式．‎ 2. 设，是两个不共线的向量，，，，若A，B，D三点共线，则实数k的值为______．‎ ‎【答案】‎ ‎【解析】【分析】‎ 本题考查实数值的求法，考查共线向量的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题求出，由A，B，D三点共线，知，由此能求出实数k的值．‎ ‎【解答】‎ 解：，是两个不共线的向量，，，‎ ‎，‎ ‎，B，D三点共线，，‎ ‎，解得．‎ 实数k的值为．‎ 故答案为．‎ 3. 在中，且，则角C的大小为______ ．‎ ‎【答案】‎ ‎【解析】解：由正弦定理有：，‎ 由余弦定理有：‎ 又 由得，‎ 又，‎ ‎．‎ 故答案为．‎ 利用正弦定理与余弦定理可求得，从而可求得角C的值．‎ 本题考查正弦定理与余弦定理，考查代换与解方程的能力，属于中档题．‎ 三、解答题（本大题共6小题，共70.0分）‎ 1. 已知不共线向量与，，，‎ 若，求m的值；‎ 若向量与共线，求m的值．‎ ‎【答案】解：不共线向量与，，，‎ ‎，‎ ‎，‎ ‎，‎ 解得．‎ ‎，，‎ 向量与共线，‎ ‎，‎ 解得．‎ ‎【解析】求出，由，能求出m．‎ 坟出，，由向量与共线，能求出m．‎ 本题考查实数值的求法，考查向量坐标运算法则、向量垂直、向量共线等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．‎ 1. 如图，在中，已知，D是BC边上的一点，，，．‎ 求的面积；‎ 求边AB的长．‎ ‎【答案】解：在中，由余弦定理得，‎ ‎，‎ 那么：，‎ 则．‎ 在中，，，‎ 由正弦定理得：，‎ ‎．‎ ‎【解析】在中，根据余弦定理求解，可得，即可求解的面积；‎ 在中，，  由正弦定理得AB的长度：‎ 本题考查了正余弦定理的应用，考查了推理能力与计算能力，属于基础题．‎ 2. 已知点和向量 若向量与向量同向，且，求点B的坐标；‎ 若向量与向量的夹角是钝角，求实数k的取值范围．‎ ‎【答案】解：设，则，‎ 若向量与向量同向，则有，‎ 若，则，‎ 解可得或，‎ 当时，，与向量反向，不合题意，舍去；‎ 当时，，与向量同向，‎ 则B的坐标为；‎ 若向量与向量的夹角是钝角，‎ 则有且，‎ 解可得且，‎ 故k的取值范围是．‎ ‎【解析】根据题意，设，易得向量的坐标，分析可得且，解可得x、y的值，验证向量与向量是否同向，即可得答案；‎ 根据题意，由向量数量积的计算公式可得且，解可得k的取值范围，即可得答案．‎ 本题考查向量数量积的计算，关键是掌握向量数量积的坐标计算公式．‎ 1. 如图，A、B是海面上位于东西方向相距海里的两个观测点，现位于A点北偏东，B点北偏西的D点有一艘轮船发出求救信号，位于B点南偏西且与B点相距海里的C点的救援船立即从C处出发沿直线CD航行前往营救，其航行速度为30海里小时，试求：‎ 轮船D与观测点B的距离；‎ 救援船到达D点所需要的时间．‎ ‎【答案】解：由D在A的北偏东，在B的北偏西，‎ ‎，， ‎ ‎；‎ 由正弦定理得， ‎ ‎；‎ 又， ‎ ‎； ‎ 答：轮船D与观测点B的距离为海里； ‎ 中，，，，‎ ‎， ‎ ‎，解得；‎ 小时；‎ 答：救援船到达D所需的时间为1小时 ‎【解析】由方向坐标求得、，‎ 利用三角形内角和定理与正弦定理求得BD的值；‎ 中，利用余弦定理求得DC的值，‎ 再计算救援船到达D所需的时间．‎ 本题考查了正弦、余弦定理的实际应用问题，是基础题．‎ ‎21.如图，边长为2的菱形ABCD中，，E、F分别是BC、DC的中点，G为 BF、DE的交点，若，．‎ 试用，表示；求的值．‎ ‎【答案】解：由题意若，．‎ ‎，‎ E、F分别是BC，DC的中点，G为 BF、DE的交点，‎ 所以G为的重心，，‎ 若，．‎ ‎，‎ ‎．‎ ‎【解析】利用向量的加法以及三角形的重心坐标关系推出结果即可．‎ 表示出向量，利用数量积化简求解即可．‎ 本题考查向量的数量积的应用，向量在三角形中的应用，考查计算能力．‎ 1. 在锐角中，角A，B，C的对边分别为a，b，c，且满足．求角C的大小；                              ‎ 若，求ab的取值范围．‎ ‎【答案】解：由得，‎ 即，‎ 即，‎ 因为在中，，所以，‎ 即．‎ 又因为，所以，‎ 因此，即得．‎ 为锐角三角形，‎ 故，解得，‎ 因此．‎ 所以．‎ 因此 由余弦定理，得，‎ 所以，‎ 故 解得．‎ ‎【解析】本题考查了正弦定理，两角和与差的三角函数公式，解三角形的应用，余弦定理和函数的图象与性质．‎ 利用正弦定理得，再利用两角和与差的三角函数公式得，最后利用题目条件计算得结论 利用解三角形的应用得，再利用函数的值域得，再利用余弦定理，最后计算得结论．‎