- 2021-05-13 发布 |
- 37.5 KB |
- 6页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
宁夏六盘山高级中学2020届高三下学期第1次周练卷数学(理)试题
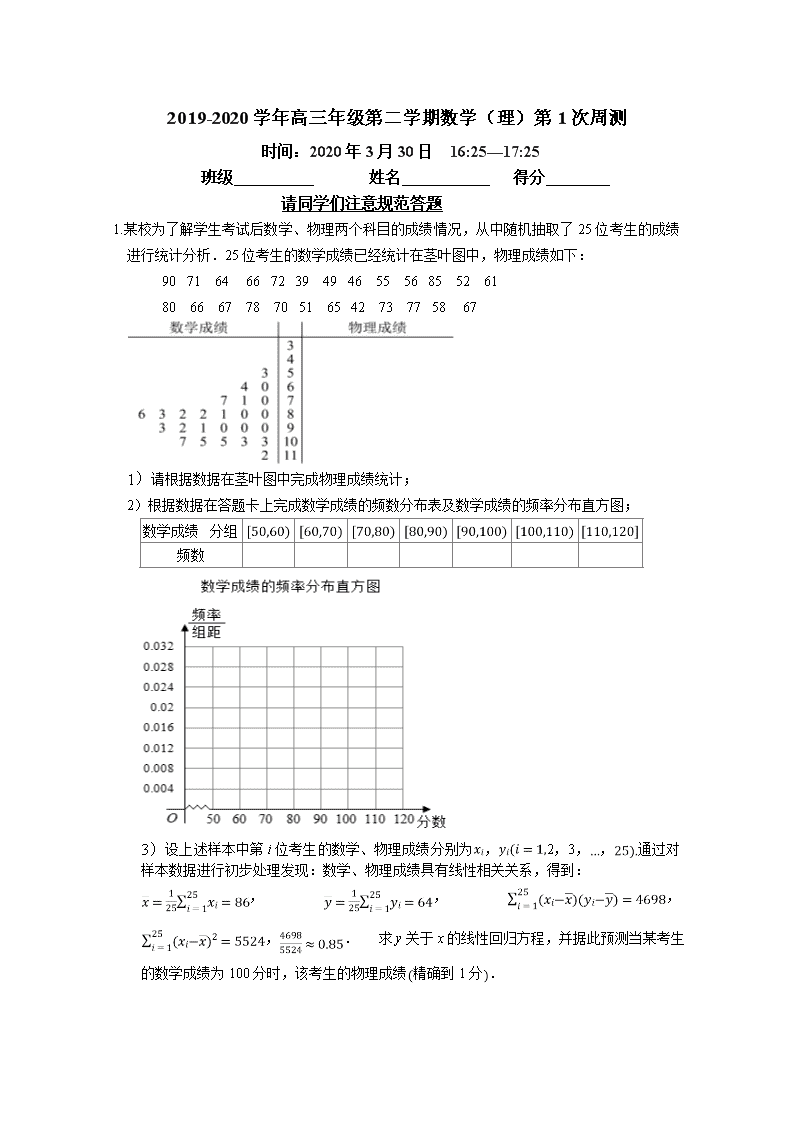
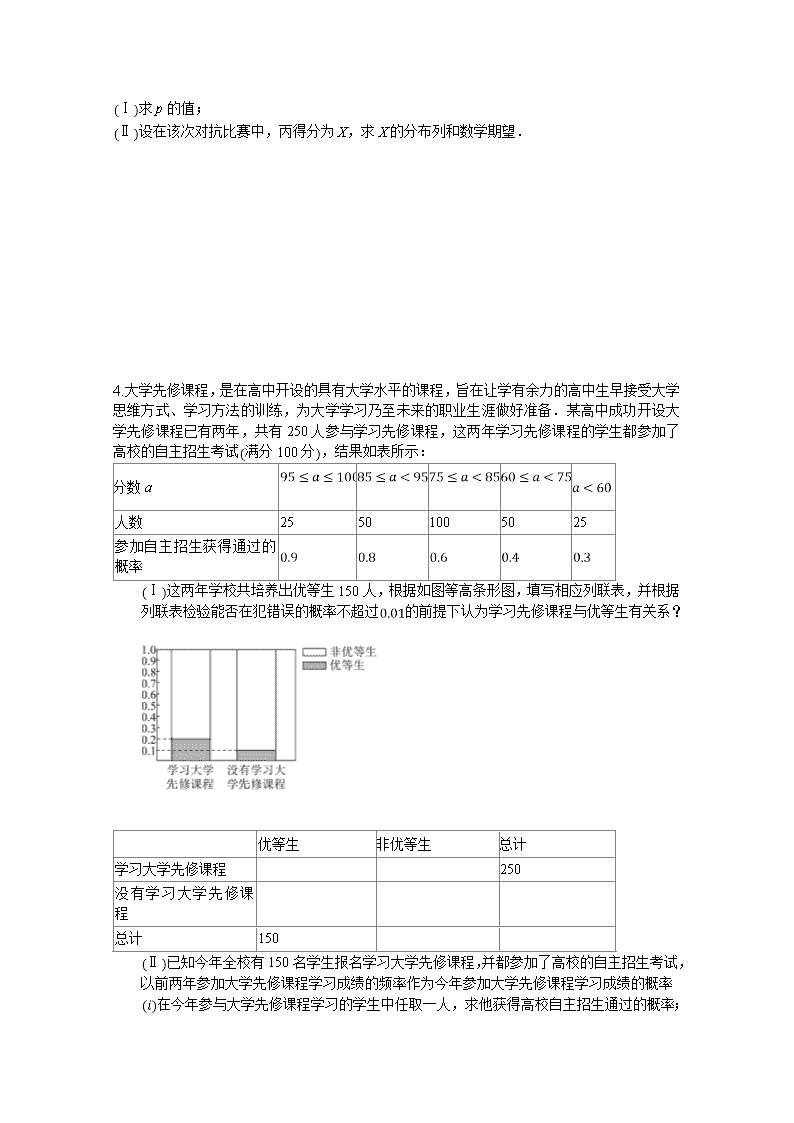
2019-2020学年高三年级第二学期数学(理)第1次周测 时间:2020年3月30日 16:25—17:25 班级 姓名 得分 请同学们注意规范答题 1.某校为了解学生考试后数学、物理两个科目的成绩情况,从中随机抽取了25位考生的成绩进行统计分析.25位考生的数学成绩已经统计在茎叶图中,物理成绩如下: 90 71 64 66 72 39 49 46 55 56 85 52 61 80 66 67 78 70 51 65 42 73 77 58 67 1)请根据数据在茎叶图中完成物理成绩统计; 2)根据数据在答题卡上完成数学成绩的频数分布表及数学成绩的频率分布直方图; 数学成绩 分组 频数 3)设上述样本中第i位考生的数学、物理成绩分别为,2,3,,通过对样本数据进行初步处理发现:数学、物理成绩具有线性相关关系,得到: ,,,,. 求y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩精确到1分 . 附:回归直线方程的斜率和截距的最小二乘估计公式分别为:,. 2. 某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为和现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立. Ⅰ求至少有一种新产品研发成功的概率; Ⅱ若新产品A研发成功,预计企业可获利润120万元;若新产品B研发成功,预计企业可获利润100万元,求该企业可获利润的分布列和数学期望. 3. 为备战2018年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单,现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得3分,负者得0分,在每一场比赛中,甲胜乙的概率为,丙胜甲的概率为,乙胜丙的概率为p,且各场比赛结果互不影响,若甲获第一名且乙获第三名的概率为. Ⅰ 求p的值; Ⅱ设在该次对抗比赛中,丙得分为X,求X的分布列和数学期望. 4.大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有250人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试满分100分,结果如表所示: 分数a 人数 25 50 100 50 25 参加自主招生获得通过的概率 Ⅰ这两年学校共培养出优等生150人,根据如图等高条形图,填写相应列联表,并根据列联表检验能否在犯错误的概率不超过的前提下认为学习先修课程与优等生有关系? 优等生 非优等生 总计 学习大学先修课程 250 没有学习大学先修课程 总计 150 Ⅱ已知今年全校有150名学生报名学习大学先修课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率 在今年参与大学先修课程学习的学生中任取一人,求他获得高校自主招生通过的概率; 某班有4名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为X,求X的分布列,试估计今年全校参加大学先修课程学习的学生获得高校自主招生通过的人数. 参考数据: 参考公式:,其中 参考答案 1.解:Ⅰ物理成绩的茎叶图如图所示: Ⅱ数学成绩的频数分布表: 数学成绩分组 频数 1 2 3 7 6 5 1 数学成绩的频率分布直方图: Ⅲ由已知得,, , 时,, 预测当某考生的数学成绩为100分时,该考生的物理成绩为76分. 2.解:Ⅰ设至少有一种新产品研发成功的事件为事件A且事件B为事件A的对立事件,则事件B为一种新产品都没有成功, 因为甲,乙研发新产品成功的概率分别为和. 则, 再根据对立事件的概率公式可得, 故至少有一种新产品研发成功的概率为. Ⅱ由题可得设企业可获得利润为X,则X的取值有0,120,100,220, 由独立试验的概率计算公式可得, , , , , 所以X的分布列如下: X 0 120 100 220 则数学期望. 3.解:Ⅰ由已知,甲获第一名且乙获第三名的概率为. 即甲胜乙、甲胜丙且丙胜乙概率为,分 ,分 Ⅱ依题意丙得分X可以为0,3,6,丙胜甲的概率为,丙胜乙的概率为分 ,,分 X 0 3 6 P 分 4.解:Ⅰ列联表如下: 优等生 非优等生 总计 学习大学先修课程 50 200 250 没有学习大学先修课程 100 900 1000 总计 150 1100 1250 由列联表可得. 在犯错误的概率不超过的前提下认为学习先修课程与优等生有关系. Ⅱ由题意得所求概率为: . 设获得高校自主招生通过的人数为X,则, ,1,2,3,4, 的分布列为: X 0 1 2 3 4 P 估计今年全校参加大学先修课程学习的学生获得高校自主招生通过的人数为.查看更多