中考压轴题4三角形相似三角形综合

中考压轴题4三角形相似三角形综合

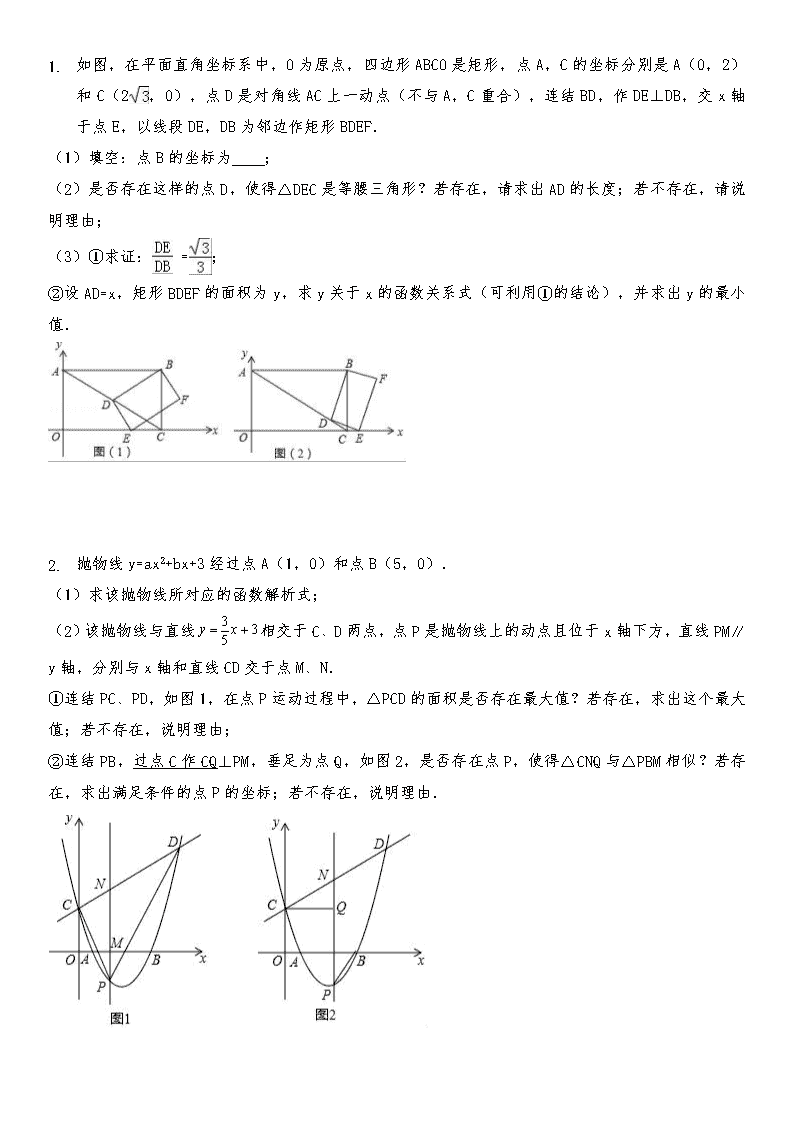
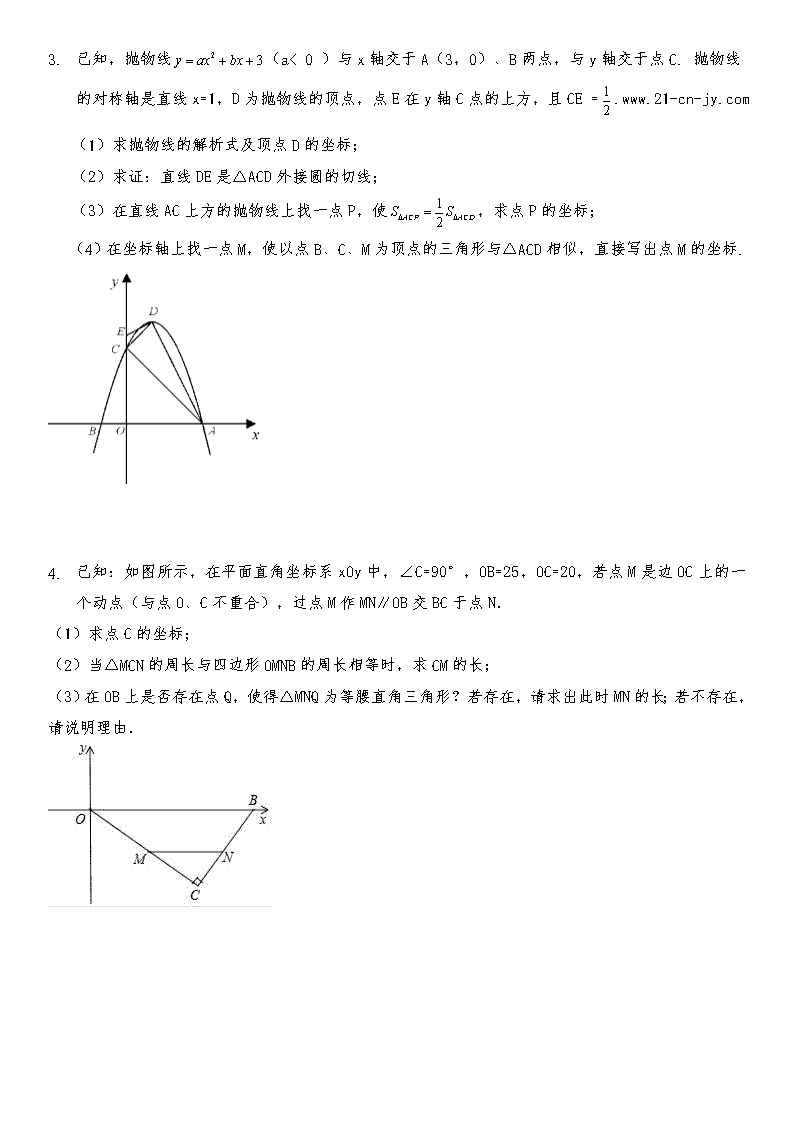
1. 如图，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A（0，2）和C（2，0），点D是对角线AC上一动点（不与A，C重合），连结BD，作DE⊥DB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF．‎ ‎（1）填空：点B的坐标为　　；‎ ‎（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长度；若不存在，请说明理由；‎ ‎（3）①求证： =；‎ ‎②设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用①的结论），并求出y的最小值．‎ 2. 抛物线y=ax2+bx+3经过点A（1，0）和点B（5，0）．‎ ‎（1）求该抛物线所对应的函数解析式；‎ ‎（2）该抛物线与直线相交于C、D两点，点P是抛物线上的动点且位于x轴下方，直线PM∥y轴，分别与x轴和直线CD交于点M、N．‎ ‎①连结PC、PD，如图1，在点P运动过程中，△PCD的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；‎ ‎②连结PB，过点C作CQ⊥PM，垂足为点Q，如图2，是否存在点P，使得△CNQ与△PBM相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由．‎ 1. 已知，抛物线（a< 0 ）与x轴交于A（3，0）、B两点，与y轴交于点C. 抛物线的对称轴是直线x=1，D为抛物线的顶点，点E在y轴C点的上方，且CE =.www.21-cn-jy.com ‎（1）求抛物线的解析式及顶点D的坐标；‎ ‎（2）求证：直线DE是△ACD外接圆的切线；‎ ‎（3）在直线AC上方的抛物线上找一点P，使，求点P的坐标；‎ ‎（4）在坐标轴上找一点M，使以点B、C、M为顶点的三角形与△ACD相似，直接写出点M的坐标.‎ 2. 已知：如图所示，在平面直角坐标系xOy中，∠C=90°，OB=25，OC=20，若点M是边OC上的一个动点（与点O、C不重合），过点M作MN∥OB交BC于点N．‎ ‎（1）求点C的坐标；‎ ‎（2）当△MCN的周长与四边形OMNB的周长相等时，求CM的长；‎ ‎（3）在OB上是否存在点Q，使得△MNQ为等腰直角三角形？若存在，请求出此时MN的长；若不存在，请说明理由．‎ 1. 已知抛物线y=ax2+bx+c，其中2a=b＞0＞c，且a+b+c=0．‎ ‎（1）直接写出关于x的一元二次方程ax2+bx+c=0的一个根；‎ ‎（2）证明：抛物线y=ax2+bx+c的顶点A在第三象限；‎ ‎（3）直线y=x+m与x，y轴分别相交于B，C两点，与抛物线y=ax2+bx+c相交于A，D两点．设抛物线y=ax2+bx+c的对称轴与x轴相交于E．如果在对称轴左侧的抛物线上存在点F，使得△ADF与△BOC相似，并且S△ADF=S△ADE，求此时抛物线的表达式．‎ 2. 如图，已知抛物线的对称轴是y轴，且点（2，2），（1，）在抛物线上，点P是抛物线上不与顶点N重合的一动点，过P作PA⊥x轴于A，PC⊥y轴于C，延长PC交抛物线于E，设M是O关于抛物线顶点N的对称点，D是C点关于N的对称点．‎ ‎（1）求抛物线的解析式及顶点N的坐标；‎ ‎（2）求证：四边形PMDA是平行四边形；‎ ‎（3）求证：△DPE∽△PAM，并求出当它们的相似比为时的点P的坐标．‎ 1. 如图，已知抛物线y=ax2+x+c与x轴交于A，B两点，与y轴交于丁C，且A（2，0），C（0，﹣4），直线l：y=﹣x﹣4与x轴交于点D，点P是抛物线y=ax2+x+c上的一动点，过点P作PE⊥x轴，垂足为E，交直线l于点F．‎ ‎（1）试求该抛物线表达式；‎ ‎（2）如图（1），过点P在第三象限，四边形PCOF是平行四边形，求P点的坐标；‎ ‎（3）如图（2），过点P作PH⊥y轴，垂足为H，连接AC．‎ ‎①求证：△ACD是直角三角形；‎ ‎②试问当P点横坐标为何值时，使得以点P、C、H为顶点的三角形与△ACD相似？‎ 2. 如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．‎ ‎（1）如图1，若BD=BA，求证：△ABE≌△DBE；‎ ‎（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AF•AC．‎ 1. 有两个内角分别是它们对角的一半的四边形叫做半对角四边形． ‎ ‎(1)如图1，在半对角四边形ABCD中，∠B＝ ∠D，∠C＝ ∠A，求∠B与∠C的度数之和； 21*cnjy*com ‎(2)如图2，锐角△ABC内接于⊙O，若边AB上存在一点D，使得BD＝BO．∠OBA的平分线交OA于点E，连结DE并延长交AC于点F，∠AFE＝2∠EAF．求证：四边形DBCF是半对角四边形； ‎ ‎(3)如图3，在（2）的条件下，过点D作DG⊥OB于点H，交BC于点G．当DH＝BG时，求△BGH与△ABC的面积之比． ‎ 1. 已知抛物线c1的顶点为A（﹣1，4），与y轴的交点为D（0，3）．‎ ‎（1）求c1的解析式；‎ ‎（2）若直线l1：y=x+m与c1仅有唯一的交点，求m的值；‎ ‎（3）若抛物线c1关于y轴对称的抛物线记作c2，平行于x轴的直线记作l2：y=n．试结合图形回答：当n为何值时，l2与c1和c2共有：①两个交点；②三个交点；③四个交点；‎ ‎（4）若c2与x轴正半轴交点记作B，试在x轴上求点P，使△PAB为等腰三角形．‎ 2. 如图1，点A坐标为（2，0），以OA为边在第一象限内作等边△OAB，点C为x轴上一动点，且在点A右侧，连接BC，以BC为边在第一象限内作等边△BCD，连接AD交BC于E．‎ ‎（1）①直接回答：△OBC与△ABD全等吗？‎ ‎②试说明：无论点C如何移动，AD始终与OB平行；‎ ‎（2）当点C运动到使AC2=AEAD时，如图2，经过O、B、C三点的抛物线为y1．试问：y1上是否存在动点P，使△BEP为直角三角形且BE为直角边？若存在，求出点P坐标；若不存在，说明理由；‎ ‎（3）在（2）的条件下，将y1沿x轴翻折得y2，设y1与y2组成的图形为M，函数y=x+m的图象l与M有公共点．试写出：l与M的公共点为3个时，m的取值．‎ 1. 如图1，经过原点的抛物线与轴交于另一点，在第一象限内与直线交于点．‎ ‎（1）求这条抛物线的表达式；‎ ‎（2）在第四象限内的抛物线上有一点，满足以为顶点的三角形的面积为2，求点的坐标；%]‎ ‎（3）如图2，若点在这条抛物线上，且，在（2）的条件下，是否存在点，使得∽?若存在，求出点的坐标；若不存在，请说明理由．‎