- 2021-05-12 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2014高考数学新人教A版大一轮复习特训 立体几何 Word版含解析
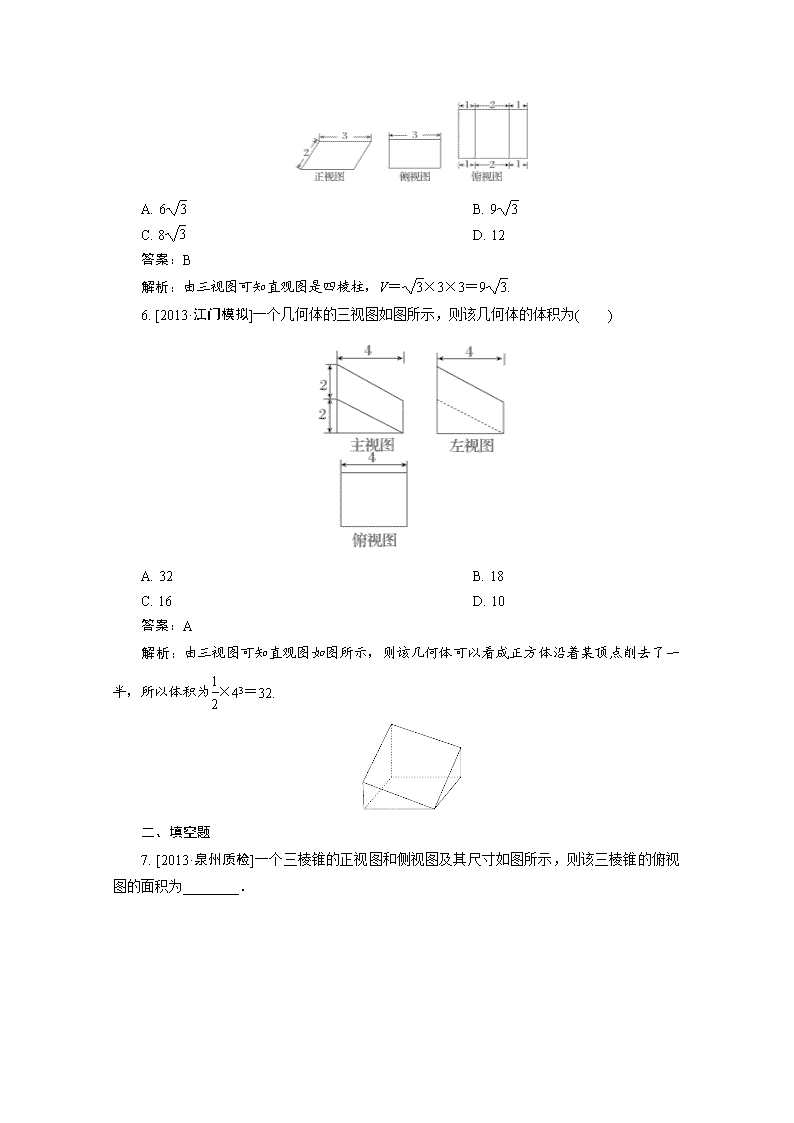
第七章 第2讲 (时间:45分钟 分值:100分) 一、选择题 1. [2013·福建质检]某几何体的三视图如图所示,且该几何体的体积是,则正视图中的x的值是 ( ) A. 2 B. C. D. 3 答案:C 解析:由三视图知,该几何体为四棱锥,其体积是×[×(1+2)×2]x=,故x=. 2. [2013·西安质检]右图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是( ) A. 20+3π B. 24+3π C. 20+4π D. 24+4π 答案:A 解析:根据几何体的三视图可知,该几何体是一个正方体和一个半圆柱的组合体,其中,正方体的棱长为2,半圆柱的底面半径为1,母线长为2.故该几何体的表面积为4×5+2×π+2×π=20+3π. 3. [2013·温州模拟]某几何体的正(主)视图与俯视图如图所示,侧(左)视图与正视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( ) A. B. C. 6 D. 4 答案:A 解析:由三视图得几何体的直观图如图所示, 其构成是一个正方体的上方除掉了一个正四棱锥, 故V=23-×22×1=. 4. 一个几何体的三视图如图所示,则这个几何体的表面积为( ) A. 6+ B. 6+2 C. 8+ D. 8+2 答案:D 解析:由三视图知,该几何体是一个底面为直角三角形的直棱柱,其表面积等于2×(×1×2)+(2×+1×2+2×2)=8+2,选D. 5. 如图,某几何体的正视图是平行四边形,侧视图和俯视图都是矩形,则该几何体的体积为( ) A. 6 B. 9 C. 8 D. 12 答案:B 解析:由三视图可知直观图是四棱柱,V=×3×3=9. 6. [2013·江门模拟]一个几何体的三视图如图所示,则该几何体的体积为( ) A. 32 B. 18 C. 16 D. 10 答案:A 解析:由三视图可知直观图如图所示,则该几何体可以看成正方体沿着某顶点削去了一半,所以体积为×43=32. 二、填空题 7. [2013·泉州质检]一个三棱锥的正视图和侧视图及其尺寸如图所示,则该三棱锥的俯视图的面积为________. 答案:1 解析:由题意可知,该三棱锥的俯视图是一个底为2,高为1的三角形,则其面积为1. 8. 某旋转体中间被挖掉一部分后,剩下部分的三视图如图所示,则该几何体的体积为________. 答案:π 解析:由三视图可知,该几何体是一个圆柱挖去一个球,圆柱的底面半径为,高为2,球的半径为,V=π×()2×2-π×()3=π. 9. [2013·青岛模拟]若一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为________. 答案:π 解析:由正视图知,三棱柱的底面边长为2,高为1,外接球的球心在上下两个三角形中心连线的中点上,连接球心和任意一个顶点的线段长为球的半径,则R2= ()2+()2=(其中R为球的半径).则球的表面积S=4πR2=4π×=π. 三、解答题 10. 如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm). (1)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积. 解:(1)如图. (2)所求多面体的体积 V=V长方体-V正三棱锥=4×4×6-×(×2×2)×2=(cm3). 11. [2013·山东模拟] 已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.求 (1)该几何体的体积V; (2)该几何体的侧面积S. 解:由三视图可知,该几何体底面是边长为8和6的矩形,高为4.顶点在底面射影恰为底面矩形的中心的四棱柱.如图,E、F分别为CD、BC的中点,易求PE=4,PF=5. ∴(1)V=S矩形ABCD·PO=×6×8×4=64. (2)S=2×(BC·PF+CD·PE) =2×(×8×5+×6×4)=40+24. 12. [2013·吉林模拟]一几何体按比例绘制的三视图如图所示(单位:m): (1)试画出它的直观图; (2)求它的表面积和体积. 解:(1)直观图如图所示. (2)由三视图可知该几何体是长方体被截去一个角,且该几何体的体积是以A1A,A1D1,A1B1为棱的长方体的体积的, 在直角梯形AA1B1B中,作BE⊥A1B1于E, 则四边形AA1EB是正方形, ∴AA1=BE=1, 在Rt△BEB1中,BE=1,EB1=1, ∴BB1=, ∴几何体的表面积 S=S正方形ABCD+S矩形A1B1C1D1+2S梯形AA1B1B+S矩形BB1C1C+S正方形AA1D1D =1+2×1+2××(1+2)×1+1×+1=7+(m2). ∴几何体的体积V=×1×2×1=(m3), ∴该几何体的表面积为(7+) m2,体积为 m3.查看更多