- 2021-05-12 发布 |
- 37.5 KB |
- 5页


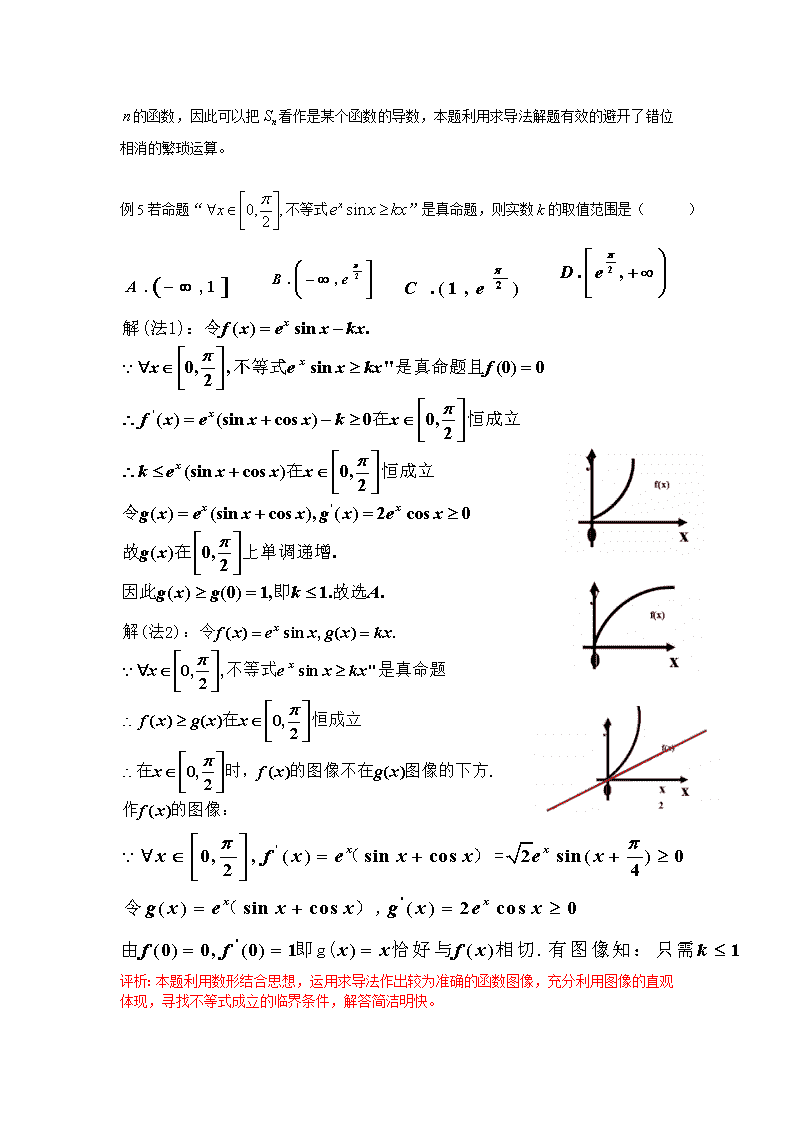
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习求导法学案(全国通用)
求 导 法 一、内容概述 求导法之所以成为高中阶段必须掌握的基本办法和技能,是基于求导法在函数问题中应用广泛,许多函数不等式或相关的函数问题都需借助求导法,通过判断单调性,通过分析单调区间、最值、极值等函数性质加以解决。 评析:利用求导法判断函数单调性寻求最值,方法直接简洁。 评析:求函数值域是中学教学中的难点,一般可以通过观察图像或不等式性质来解,也可以通过函数单调性求最值,本题形式较为复杂,较难作出函数图像,可采用求导法判断函数的单调性来解。 评析:利用求导法证明不等式,关键是如何根据不等式的结构特征构造辅助函数(函数与方程思想),把不等式的证明转化为利用导数研究函数的单调性或最值,从而证明不等式。 评析: 数列是一种特殊的函数,它有通项公式和前项和公式,并且和都是关于 的函数,因此可以把看作是某个函数的导数,本题利用求导法解题有效的避开了错位相消的繁琐运算。 例5若命题“不等式”是真命题,则实数的取值范围是( ) 评析:本题利用数形结合思想,运用求导法作出较为准确的函数图像,充分利用图像的直观体现,寻找不等式成立的临界条件,解答简洁明快。 练习题 1若函数在单调递增,则a的取值范围。 2.利用导数求和: 3. 利用求导法证明下列不等式 (1)已知:,求证; (2)已知:,求证:。 参考答案 1. 解析:此题考察恒成立问题,对原函数求导可得,若原函数在R上单调递增,则恒成立,设,,分别带入和,解得. 2.解析:∵, 两边都是关于x的函数,求导得。 令x=1得 , 即证。 3.解析(1)令,由x>0,∴t>1, 原不等式等价于 令f(t)=t-1-lnt, ∵当时,有,∴函数f(t)在递增 ∴f(t)>f(1) 即t-1查看更多