中考数学填空题专项训练
中考数学填空题专项训练(一)
二、填空题(每小题3分,共21分)
9. 写出一个大于的负整数___________.
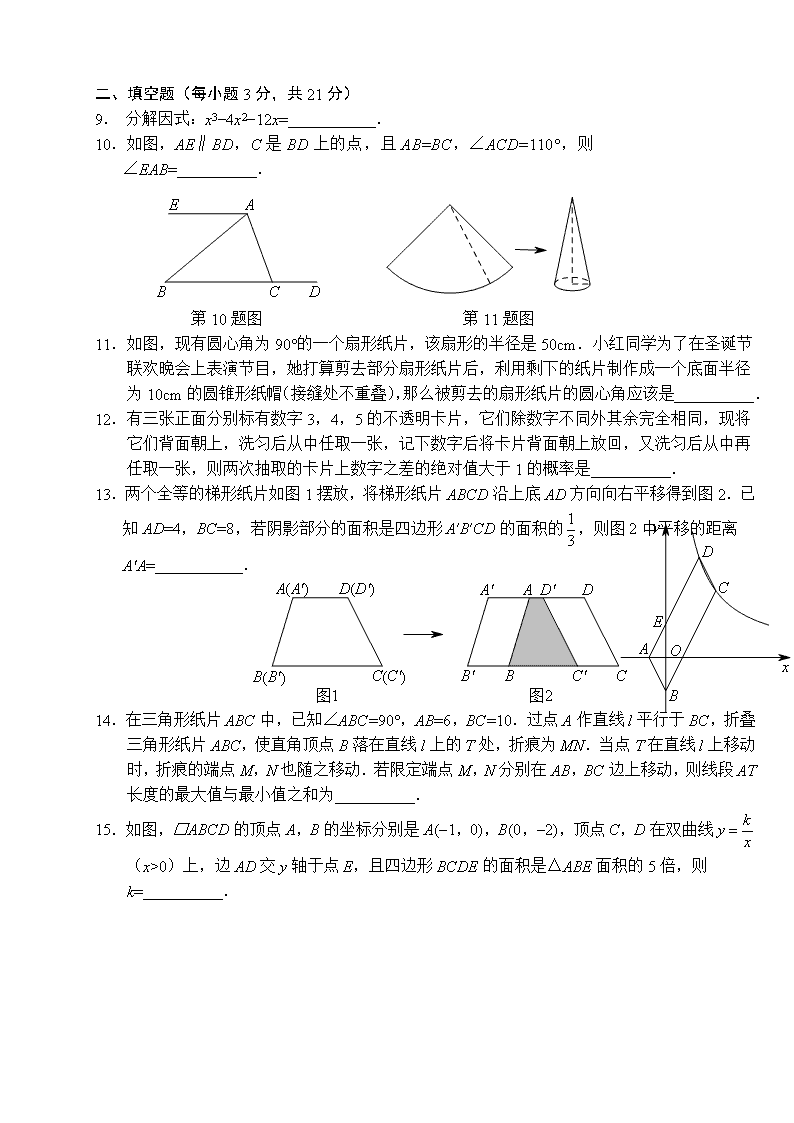
10. 如图,在△ABC中,∠C=90°,若BD∥AE,∠DBC=20°,则∠CAE的度数是___________.
第10题图 第11题图 第12题图 第13题图
11. 如图,一次函数y1=ax+b(a≠0)与反比例函数的图象交于A(1,4),B(4,1)两点,若使y1>y2,则x的取值范围是___________.
12. 在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是___________.
13. 如图所示,正方形ABCD内接于⊙O,直径MN∥AD,则阴影部分面积占圆面积的____________.
14. 如图,在五边形ABCDE中,∠BAE=125°,∠B=∠E=90°,AB=BC,AE=DE,在BC,DE上分别找一点M,N,使得△AMN周长最小时,∠AMN+∠ANM的度数为__________.
15. 已知□ABCD的周长为28,自顶点A作AE⊥DC于点E,AF⊥BC于点F.若AE=3,AF=4,则CE-CF=____________.
中考数学填空题专项训练(二)
二、填空题(每小题3分,共21分)
9. 分解因式:x3-4x2-12x=___________.
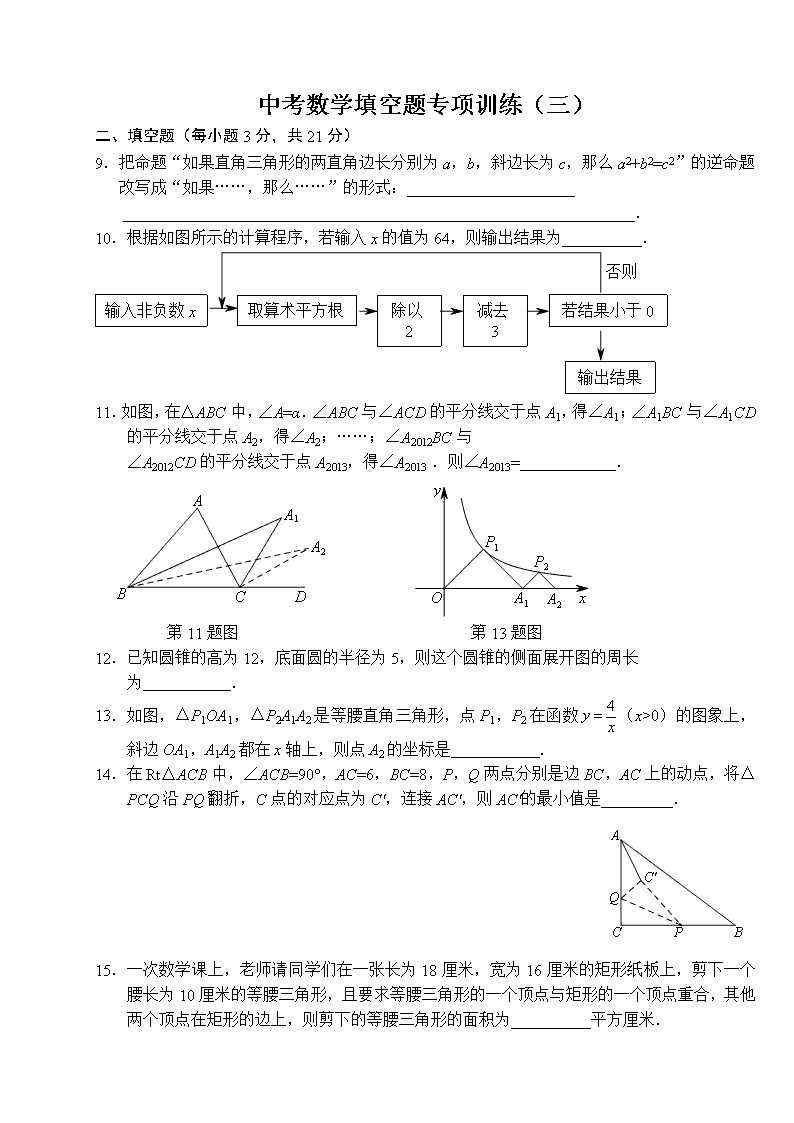
10. 如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则
∠EAB=__________.
第10题图 第11题图
11. 如图,现有圆心角为90°的一个扇形纸片,该扇形的半径是50cm.小红同学为了在圣诞节联欢晚会上表演节目,她打算剪去部分扇形纸片后,利用剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),那么被剪去的扇形纸片的圆心角应该是__________.
12. 有三张正面分别标有数字3,4,5的不透明卡片,它们除数字不同外其余完全相同,现将它们背面朝上,洗匀后从中任取一张,记下数字后将卡片背面朝上放回,又洗匀后从中再任取一张,则两次抽取的卡片上数字之差的绝对值大于1的概率是__________.
13. 两个全等的梯形纸片如图1摆放,将梯形纸片ABCD沿上底AD方向向右平移得到图2.已知AD=4,BC=8,若阴影部分的面积是四边形A′B′CD的面积的,则图2中平移的距离A′A=___________.
14. 在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=10.过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直线l上移动时,折痕的端点M,N也随之移动.若限定端点M,N分别在AB,BC边上移动,则线段AT长度的最大值与最小值之和为__________.
15. 如图,□ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),顶点C,D在双曲线(x>0)上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k=__________.
中考数学填空题专项训练(三)
二、填空题(每小题3分,共21分)
9. 把命题“如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2”的逆命题改写成“如果……,那么……”的形式:_____________________
________________________________________________________________.
否则
输出结果
若结果小于0
输入非负数x
10. 根据如图所示的计算程序,若输入x的值为64,则输出结果为__________.
取算术平方根
除以2
减去3
11. 如图,在△ABC中,∠A=α.∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线交于点A2,得∠A2;……;∠A2012BC与
∠A2012CD的平分线交于点A2013,得∠A2013 .则∠A2013= .
第11题图 第13题图
12. 已知圆锥的高为12,底面圆的半径为5,则这个圆锥的侧面展开图的周长为 .
13. 如图,△P1OA1,△P2A1A2是等腰直角三角形,点P1,P2在函数(x>0)的图象上,斜边OA1,A1A2都在x轴上,则点A2的坐标是 .
14. 在Rt△ACB中,∠ACB=90°,AC=6,BC=8,P,Q两点分别是边BC,AC上的动点,将△PCQ沿PQ翻折,C点的对应点为C′,连接AC′,则AC′的最小值是_________.
15. 一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其他两个顶点在矩形的边上,则剪下的等腰三角形的面积为__________平方厘米.
中考数学填空题专项训练(四)
二、填空题(每小题3分,共21分)
9. =___________.
10. 如图,在平行四边形ABCD中,DB=DC,∠A=65°,CE⊥BD于点E,则
∠BCE=_____________.
第10题图 第11题图
11. 如图,菱形ABCD的边长为2cm,∠A=60°.弧BD是以点A为圆心、AB长为半径的弧,弧CD是以点B为圆心、BC长为半径的弧.则阴影部分的面积为___________.
12. 哥哥与弟弟玩一个游戏:三张大小、质地都相同的卡片上分别标有数字1,2,3,将标有数字的一面朝下,哥哥从中任意抽取一张,记下数字后放回洗匀,然后弟弟从中任意抽取一张,计算抽得的两个数字之和,如果和为奇数,则弟弟胜,如果和为偶数,则哥哥胜.该游戏对双方__________(填“公平”或“不公平” ).
13. 如图,在等边三角形ABC中,点O在AC上,且AO=3,CO=6,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°,得到线段OD.要使点D恰好落在BC上,则AP的长是_______.
14. 如图,直线与y轴交于点A,与双曲线在第一象限交于B,C两点,且AB·AC=4,则k=__________.
15. 小明尝试着将矩形纸片ABCD(如图1,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图2);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图3).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD长与宽的比值为___________.
中考数学填空题专项训练(五)
二、 填空题(每小题3分,共21分)
9. 请写出一个二元一次方程组______________,使它的解是.
10. 如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC=__________.
第10题图 第13题图
11. 如果圆锥的底面周长是20π,侧面展开后所得的扇形的圆心角为120°,那么圆锥的母线长是__________.
12. 在不透明的口袋中,有四个形状、大小、质地完全相同的小球,四个小球上分别标有数字,2,4,,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数图象上,则点P落在正比例函数y=x图象上方的概率是__________.
13. 如图,在等边三角形ABC中,D是BC边上的一点,延长AD至E,使AE=AC,∠BAE的平分线交△ABC的高BF于点O,则tan∠AEO=_________.
14. 如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则矩形ABCD的面积为_______.
第14题图 第15题图
9. 如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x轴于点H.在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是____________________________________.
中考数学填空题专项训练(六)
二、填空题(每小题3分,共21分)
9. 计算:=________.
10. 如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A′处,若∠A′BC=15°,则∠A′BD的度数为__________.
第10题图 第11题图 第13题图
11. 如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 _________(结果保留π).
12. 有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字-2,-3和-4.小明从A布袋中随机取出一个小球,记其标有的数字为x,再从B布袋中随机取出一个小球,记其标有的数字为y,则满足x+y=-2的概率是 .
13. 如图,直线y=kx-2(k>0)与双曲线在第一象限内的交点为R,与x轴、y轴的交点分别为P,Q.过R作RM⊥x轴,垂足为M,若△OPQ与△PRM的面积相等,则k的值为________.
14. 已知菱形ABCD的边长是8,点E在直线AD上,若DE=3,连接BE,与对角线AC相交于点M,则的值是_________.
15. 在矩形ABCD中,AB=3,AD=4,将其沿对角线BD折叠,顶点C的对应位置为G(如图1),BG交AD于E;再折叠,使点D落在点A处,折痕MN交AD于F,交DG于M,交BD于N,展开后得图2,则折痕MN的长为___________.
中考数学填空题专项训练(七)
二、填空题(每小题3分,共21分)
9. 方程的解为___________.
10. 如图,在菱形ABCD中,点E,F分别是BD,CD的中点,若EF=6cm,则AB=____________cm.
第10题图 第11题图
11. 王红和刘芳两人在玩转盘游戏,如图,把转盘甲、乙分别分成3等份,并在每一份内标上数字,游戏规则是:转动两个转盘,停止后指针所指的两个数字之和为7时,王红胜;数字之和为8时,刘芳胜.那么这二人中获胜可能性较大的是___________.
12. 如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数(k>0)的图象与正方形的一个交点.若图中阴影部分的面积等于9,则该反比例函数的解析式为_________.
第12题图 第13题图
13. 如图所示,正方形ABCD中,E是AD边上一点,以E为圆心、ED为半径的半圆与以B为圆心、BA为半径的圆弧外切,则sin∠EBA的值为_________.
14. 如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是_______________.
第14题图 第15题图
9. 如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,2),将矩形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E.那么点D的坐标为__________________.
中考数学填空题专项训练(八)
二、填空题(每小题3分,共21分)
9. -2tan45°=_____________.
10. 如图所示,四边形ABCD中,AE,AF分别是BC,CD的垂直平分线,∠EAF=80°,∠CBD=30°,则∠ABC的度数为______________.
11. 数学老师布置10道选择题作业,批阅后得到如下统计表.根据表中数据可知,这45名同学答对题数组成的样本的中位数是________题.
答对题数
7
8
9
10
人数
4
18
16
7
12. 二次函数y=-(x-2)2+的图象与x轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有___________个.(提示:必要时可利用下面的备用图画出图象来分析)
第12题图 第13题图
13. 如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为______________.
14. 如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为_______________.
第14题图 第15题图
15. 如图,在矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点B落在边AD上的点处,折痕为CE.在折痕CE上存在一点P到边AD的距离与到点B的距离相等,则此相等距离为______________.
中考数学填空题专项训练(九)
二、填空题(每小题3分,共21分)
9. 在数轴上与表示的点的距离最近的整数点所表示的数是________.
10. 如图所示,已知O是四边形ABCD内一点,OB=OC=OD,∠BCD=∠BAD=75°,则∠ADO+∠ABO=________.
第10题图 第13题图
11. 已知在△ABC中,AB=6,AC=8,∠A=90°,把Rt△ABC绕直线AC旋转一周得到一个圆锥,其表面积为S1,把Rt△ABC绕直线AB旋转一周得到另一个圆锥,其表面积为S2,则S1:S2等于________.
12. 有四张正面分别标有数字-3,0,1,5的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使关于x的分式方程有正整数解的概率为_______.
13. 如图,直线与双曲线(x>0)交于点A.将直线向右平移个单位后,与双曲线(x>0)交于点B,与x轴交于点C,若,则k=_____.
14. 如图,在等腰Rt△ABC中,∠A=90°,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转90°,得到线段OD,要使点D恰好落在BC上,AP的长度为__________.
第14题图 第15题图
15. 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P
的运动过程中,使△PMC为等腰三角形的点P有__________个.
中考数学填空题专项训练(十)
二、填空题(每小题3分,共21分)
9. 计算:=___________.
10. 如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于_________.
第10题图 第11题图
11. 如图,将△ABC绕点B逆时针旋转到△A′BC′,使A,B,C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则线段AC扫过的面积是_________.
12. 甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为a,再由乙猜甲刚才所想数字,把乙所猜数字记为b,且a,b分别取0,1,2,3,若a,b满足|a-b|≤1,则称甲、乙两人“心有灵犀”.现任意找两人玩这个游戏,得出“心有灵犀”的概率为___________.
13. 如图,已知AB=12,AB⊥BC于点B,AB⊥AD于点A,AD=5,BC=10.若点E是CD的中点,则AE的长是___________.
14. 如图,正方形OABC的面积是4,点B在反比例函数(k>0,x<0)的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足分别为M,N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S,则当S=m(m为常数,且0
0),(x>0),点P为双曲线上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA,PB分别交双曲线于D,C两点,则△PCD的面积为______.
14. 如图,正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,且始终保持AM⊥MN.当BM=______时,四边形ABCN的面积最大.
第14题图 第15题图
15. 一个自然数的立方可以分裂成若干个连续奇数的和,例如:23,33和43分别可以按如图所示的方式“分裂”出2个、3个和4个连续奇数的和,即23=3+5,33=7+9+11,43=13+15+17+19,…,若63
也按照此规律进行“分裂”,则“分裂”出的奇数中,最大的那个奇数是______.
中考数学填空题专项训练(十五)
二、填空题(每小题3分,共21分)
9. 写出一个在实数范围内能用平方差公式分解因式的多项式:_____________.
10. 如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转180°得到△FEC,连接AE,BF.当∠ACB为_________度时,四边形ABFE为矩形.
第10题图 第11题图 第12题图
11. 如图所示,A,B是边长为1的小正方形组成的5×5网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是_________.
12. 如图,Rt△ABC中,∠ACB=90°,∠B=30°,AB=12cm,以AC为直径的半圆O交AB于点D,点E是AB的中点,CE交半圆O于点F,则图中阴影部分的面积为________.
13. 如图,以等腰Rt△ABC的斜边AB为边作等边△ABD,C,D在AB的同侧,连接DC,以DC为边作等边△DCE,B,E在CD的同侧.若AB=,则BE=_______.
14. 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=_________.
第14题图 第15题图
9. 如图,P是抛物线对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x,抛物线交于A,B两点.若△ABP是以点A或点B为直角顶点的等腰直角三角形,则满足条件的t值为______________________.
中考数学填空题专项训练(十六)
二、填空题(每小题3分,共21分)
9. 当x=_______时,分式无意义.
10. 两位同学在描述同一反比例函数的图象时,甲同学说:“从这个反比例函数图象上任意一点向x轴,y轴作垂线,与两坐标轴所围成的矩形的面积为6”,乙同学说:“这个反比例函数图象与直线y=-x有两个交点”.则这两位同学所描述的反比例函数的表达式为_____________.
11. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.若∠ACD=114°,则∠MAB的度数为__________.
第11题图 第13题图
12. 小刚、小强、小红利用假期到某个社区参加义务劳动,为决定到哪个社区,他们约定用“剪刀、石头、布”的方式确定,则在同一回合中,三人都出剪刀的概率是_______.
13. 如图,在△ABC中,∠ACB=90°,以AC为一边在△ABC外侧作等边△ACD,过点D作DE⊥AC,垂足为F,DE与AB相交于点E,连接CE,AB=15cm,BC=9cm,P是射线DE上的一点.连接PC,PB,则△PBC周长的最小值为_______.
14. 如图,在矩形ABCD中,AB=6,BC=8,E是BC边上的一定点,P是CD边上的一动点(不与点C,D重合),M,N分别是AE,PE的中点.在点P运动的过程中,MN的长度不断变化,设MN=d,则d的变化范围是_______.
第14题图 第15题图
9. 如图,点M是直线y=2x+3上的动点,过点M作MN⊥x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形?小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,△MNP为等腰直角三角形.请你写出y轴上其他符合条件的点P的坐标__________________.
中考数学填空题专项训练(十七)
二、填空题(每小题3分,共21分)
9. 函数的自变量x的取值范围是__________.
10. 如图,AB∥CD,EF与AB,CD分别相交于点E,点F,∠BEF的平分线EG交CD于点G,若∠1=50°,则∠2=__________度.
第10 题图 第11题图 第13题图
11. 如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为___________.
12. 在一个不透明的盒子里装有5个分别写有数字-2,-1,0,1,2的小球,它们除数字不同外其余全部相同.现从盒子里随机取出一个小球,将该小球上的数字作为点P的横坐标,将该数的平方作为点P的纵坐标,则点P落在抛物线y=-x2+2x+5与x轴所围成的区域内(不含边界)的概率是___________.
13. 已知:如图,直线与双曲线(x<0)相交于A,B两点,与x轴、y轴分别相交于D,C两点,若AB=5,则k=__________.
14. 如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点运动到端点时,另一个动点也随之停止运动,那么,当以A,P,Q为顶点的三角形与△ABC相似时,运动时间为_________秒.
15. 已知:如图,AB=10,点C,D在线段AB上,且AC=DB=2,P是线段CD上的动点,分别以AP
,PB为边在线段AB的同侧作等边三角形AEP和等边三角形PFB,连接EF,设EF的中点为点G.当点P从点C运动到点D时,点G移动的路径长是___________.
二、填空题(每小题3分,共21分)
9. 计算:=____________.
10. 如图,直线a∥b,直线l分别与a,b交于E,F两点,FP平分∠EFD,交a于P点,若∠1=70°,则∠2=___________.
第10题图 第12题图
11. 已知圆锥的底面直径和母线长都是10cm,则圆锥的侧面积为_________.
12. “五一”黄金周期间,梁先生驾驶汽车从甲地经过乙地到丙地游玩.甲地到乙地有2条公路,乙地到丙地有3条公路,每一条公路的长度如图所示(单位:km).梁先生任选一条从甲地到丙地的路线,这条路线正好是最短路线的概率是________.
13. 如图,正方形ABCD的顶点C,D均在双曲线的第一象限分支上,顶点A,B分别在x轴、y轴上,则此正方形的边长为_______.
14. 动手操作:在一张长12cm、宽5cm的矩形纸片内折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH(图1),小明同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB,从而折出菱形AECF(图2).则小颖和小明同学的折法中,________折出的菱形面积较大(填“小颖”或“小明”).
15. 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,P点的坐标为_______.
中考数学填空题专项训练(十九)
二、填空题(每小题3分,共21分)
9. 已知方程xy=16,写出两对满足此方程的x与y的值______________.
10. 如图,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC=____度.
第10题图 第13题图
11. 在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:对于多项式x4-y4,因式分解的结果是(x-y)(x+y)(x2+y2),若取x=9,y=9,则各个因式的值是:(x-y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3-xy2,取x=10,y=10时,用上述方法产生的密码可能是_______.(写出一个即可)
12. 某校举行以“保护环境,从我做起”为主题的演讲比赛.经预赛,七、八年级各有一名同学进入决赛,九年级有两名同学进入决赛.前两名都是九年级同学的概率是________.
13. 如图,反比例函数(x>0)的图象经过矩形OABC对角线的交点M,分别与AB,BC相交于点D,E.若四边形ODBE的面积为6,则k的值为________.
14. 如图,把矩形ABCD对折,折痕为MN(图1),展开后再折叠,使点B落在折痕MN上的B′处,得到Rt△AB′E(图2),延长EB′交AD于F,则
∠EFA=________.
第14题图 第15题图
15. 如图所示,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发,沿着A→B→A的方向运动,设运动时间为t(s)(0≤t<3),连接EF,当t为________s时,△BEF是直角三角形.
中考数学填空题专项训练(二十)
二、填空题(每小题3分,共21分)
9. 分解因式:=________________.
10. 如图,AB∥CD,EG⊥AB,垂足为G.若∠1=50°,则∠E=_______.
第10题图 第11题图 第12题图
11. 一个几何体由圆锥和圆柱组成,其尺寸如图所示,则该几何体的全面积(即表面积)为_______.(结果保留π)
12. 已知菱形ABCD中,对角线AC=8cm,BD=6cm,在菱形内部(包括边界)任取一点P,得到△ACP,则△ACP的面积大于6cm2的概率为___________.
13. 身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形纸片ABCD(矩形纸片要足够长),我们按如下步骤操作可以得到一个特定的角:
(1)以点A所在直线为折痕,折叠纸片,使点B落在AD边上,折痕与BC交于点E;
(2)将纸片展平后,以E所在直线为折痕,再一次折叠纸片,使点A落在
BC上,折痕EF交AD于点F,则∠AFE=____________.
14. 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,BC=,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,垂足为点E,则DE的长为_______.
第14题图 第15题图
9. 如图是反比例函数(x>0)的图象,点C的坐标为(0,2),若点A是函数图象上一点,点B是x轴正半轴上一点,当△ABC是等腰直角三角形时,点B的坐标为___________.
中考数学填空题专项训练(二十一)
二、填空题(每小题3分,共21分)
9. 写出一个3到4之间的无理数________.
10. 如图,在直角三角形纸片ABC中,∠A=90°,剪去这个直角后得到一个四边形BEFC,则∠BEF+∠CFE的度数是_______.
第10题图 第12题图 第13题图
11. 对于平面内任意一个四边形ABCD,现从以下四个关系式:①AB=CD;
②AD=BC;③AB∥CD;④∠A=∠C中任取两个作为条件,能够得出四边形ABCD是平行四边形的概率是_______.
12. 如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域的面积是_______.
13. 如图,正方形ABCD的边AB在x轴的正半轴上,C(2,1),D(1,1).反比例函数(x>0)的图象与边BC交于点E,与边CD交于点F.若BE:CE=3:1,则DF:FC=________.
14. 如图,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A,D重合的一动点,Q是边BC上的任意一点,连接AQ,DQ,过P作PE∥DQ,交AQ于点E,作PF∥AQ,交DQ于点F,则△PEF面积的最大值是_______.
15. 已知在Rt△ABC中,∠C=90°,AC=6,BC=8,将它的一个锐角翻折,使该锐角顶点落在其对边的中点D处,折痕交另一直角边于点E,交斜边于点F,则tan∠CDE的值为
_______.
中考数学填空题专项训练(二十二)
二、填空题(每小题3分,共21分)
9. 如果在等式5(x+2)=2(x+2)的两边同除以(x+2)就会得到5=2.我们知道5≠2,由此可以猜测(x+2)等于_______.
10. 如图,在边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则tan∠APD的值是___________.
第10题图 第11题图
11. 如图,以边长为6的正三角形ABC的顶点A为圆心,作弧DE与BC相切,分别交AB,AC于点D,E,若用阴影部分围成一个圆锥,则圆锥底面半径是_______.
12. 一只不透明的箱子中放了3副黑色手套和1副白色手套,假设手套不分左右,小明从这只箱子中任意取出2只手套,恰好配成两只颜色相同的一副手套的概率是_______.
13. 如图1,矩形ABCD中,AB=3cm,BC=4cm.沿对角线AC剪开,将△ABC向右平移至△A1BC1的位置,如图2,若重叠部分的面积为3cm2,则平移的距离AA1=______.
14. 如图,正三角形ABO的顶点B的坐标为(-2,0),过点C(2,0)作直线CE交AO于点D,交AB于点E,点E在双曲线(x<0)的图象上,若S△ADE=S△OCD,则k=_____.
第14题图 第15题图
15. 将三角形纸片ABC按如图所示的方式折叠,使点B落在边AC上的点B′处,折痕为EF.已知AB=AC=3,BC=4,若以点,F,C为顶点的三角形与△ABC相似,则BF的长是________.
中考数学填空题专项训练(二十三)
二、填空题(每小题3分,共21分)
9. 数轴上表示的点与原点的距离为________.
10. 如图,将正方形纸片ABCD分别沿AE,BF折叠(点E,F是边CD上的两点),使点C与点D在正方形内重合于点P处,则∠EPF=_______.
第10题图 第11题图 第12题图
11. 如图,有一块直径为2m的圆形铁皮,要从中裁出一个圆心角为90°的最大扇形,做成一个圆锥形容器,那么这个圆锥形容器的底面直径约为_______.
(精确到0.1m)
12. 如图,一个正方形花坛分成编号为①、②、③、④的四块,现有红、黄、蓝、紫四种颜色的花供选种.要求每块只种一种颜色的花,且相邻的两块种不同颜色的花,如果编号为①的那块已经种上红色花,那么其余三块不同的种法有_______种.
13. 如图,在△ABC中,E是BC边上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF=______.
14. 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-1,0),
B(1,1),将△ABC沿x轴的正方向平移,在第一象限内B,C两点的对应点B1,C1正好落在反比例函数的图象上,则k=______.
第14题图 第15题图
9. 如图,将正三角形ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小正三角形,若,则△ABC的边长为_________.
中考数学填空题专项训练(二十四)
二、填空题(每小题3分,共21分)
9. 若关于x的方程x2-2x-m=0有两个相等的实数根,则m的值是___________.
10. 在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,如果AE=2,△ADE的面积与四边形BCED的面积之比为4:5,那么AB的长为_________.
第10题图 第11题图 第13题图
11. 已知:如图,点E是⊙O上的点,B,C分别是劣弧AD的三等分点,∠AED=69°,则∠OBC的度数为_________.
12. 小兰和小潭用掷A,B两枚骰子的方法来确定P(x,y)的位置,她们规定:小兰掷得的点数为x,小谭掷得的点数为y,那么,她们各掷一次所确定的点落在直线y=-2x+6上的概率为________.
13. 已知函数y=-x+3的图象与x轴、y轴分别交于点C,B,与双曲线交于点A,D,若AB+CD=BC,则k的值为_________.
14. 如图,在正方形ABCD中,点E在边DC上,DE=2,EC=1,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F,C两点的距离为_________.
第14题图 第15题图
9. 如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点C,D分别落在C′,D′处,且C′D′经过点B,EF为折痕,当D′E⊥AD时,的值为_________.
中考数学填空题专项训练(二十五)
二、填空题(每小题3分,共21分)
9. 函数的自变量x的取值范围是__________________.
10. 如图所示,某江段江水流向经过B,C,D三点拐弯后与原来相同,若
∠ABC=120°,∠BCD=80°,则∠CDE的度数为______________.
第10题图 第11题图
11. 如图,在平面直角坐标系中,点A是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为_____________.
12. 小江玩投掷飞镖的游戏,他设计了一个如图所示的靶子,点E,F分别是矩形ABCD的两边AD,BC上的点,EF∥AB,点M,N是EF上任意两点,则投掷一次,飞镖落在阴影部分的概率为_______________.
第12题图 第13题图
13. 以正方形ABCD的边BC为直径作半圆O,过点D作半圆O的切线,交AB边于点E,切点为F.则△ADE与直角梯形EBCD的周长之比为_______.
14. 如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,点D在AC边上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么线段DE的长为_____________.
第14题图 第15题图
15. 如图,在Rt△ABC中,∠C=90°,∠ABC=45°,AB=6,点D在AB边上,点E在BC边上(不与B,C两点重合).若DA=DE,则AD的取值范围是___________________.
中考数学填空题专项训练(二十六)
二、填空题(每小题3分,共21分)
9. 不等式组的解集是________.
10. 已知一次函数y=kx+b(k≠0)的图象经过点(0,1),且y随x的增大而增大,请你写出一个符合上述条件的函数______________.
11. 如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿EF折叠后,D,C两点分别落在点D′,C′的位置,并利用量角器量得∠EFB=65°,则∠AED′= 度.
第11题图 第12题图
12. 如图是某几何体的三视图及相关数据(单位:cm),则该几何体的表面积为_______cm2.
13. 如图,O是正方形ABCD的两条对角线BD,AC的交点,EF过点O,若图中阴影部分的面积为1,则正方形ABCD的周长为_________.
14. 如图,将Rt△ABC绕点C按顺时针方向旋转90°到△A′B′C的位置,已知斜边AB=10cm,BC=6cm,设M是A′B′的中点,连接AM,则AM=_________cm.
第14题图 第15题图
9. 如图,直线与x轴交于点A,与y轴交于点B,将此直线向上平移4个单位后与双曲线y=(x>0)交于C,D两点,若CD=2AB,则k=_________.
中考数学填空题专项训练(二十七)
二、填空题(每小题3分,共21分)
9. 计算:=_____________.
10. 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=_________.
第10题图 第12题图 第13题图
11. 小明要给刚结识的朋友小林打电话,他只记住了电话号码的前4位,后3位是3,6,8三个数字的某一种排列顺序,但具体顺序忘记了,那么小明第一次就拨通电话的概率是_________.
12. 如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,点B的坐标是___________.
13. 如图,在梯形ABCD中,AB∥CD,∠A+∠B=90°,CD=5,AB=11,点M,N分别为AB,CD的中点,则线段MN=_________.
14. 如图是某公园的一角,∠AOB=90°,弧AB的半径OA的长是8米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是_______.
第14题图 第15题图
9. 二次函数的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2013在y轴的负半轴上,B1,B2,B3,…,B2013在二次函数第三象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2012B2013A2013都为等边三角形,则△A2012B2013A2013的边长为_________.
中考数学填空题专项训练(二十八)
二、填空题(每小题3分,共21分)
9. 若不等式组的解集是x>3,则m的取值范围是___________.
10. 如图是一个上下底密封的纸盒的三视图,根据图中数据,这个密封纸盒的表面积为_______________(结果保留根号).
第10题图 第11题图 第13题图
11. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=6,Rt△AB'C'可以看作由Rt△ABC绕点A逆时针旋转60°得到的,则线段B′C的长为__________.
12. 一个口袋中有12个白球和若干个黑球,在不允许将球倒出来数的前提下,小亮为估计口袋中黑球的个数,采用了如下的方法:每次先从口袋中摸出10个球,求出其中白球数与10的比值,再把球放回口袋中摇匀.重复上述过程5次,得到的白球数与10的比值分别为:0.4,0.1,0.2,0.1,0.2.根据上述数据,小亮可估计口袋中大约有_________个黑球.
13. 如图,在平面直角坐标系中,点A的坐标为(0,2),点C是第二象限内一点,且AC=1,则∠AOC的取值范围是_____________.
14. 如图,矩形ABCD中,AB=4,BC=8,E为CD边的中点,点P,Q为BC边上两个动点,且PQ=2,当BP=_________时,四边形APQE的周长最小.
第14题图 第15题图
9. 如图所示,点A1,A2,A3在x轴上,且OA1=A1A2=A2A3,分别过点A1,A2,A3作y轴的平行线,与反比例函数(x>0)的图象分别交于点B1,B2,B3,分别过点B1,B2,B3作x轴的平行线,分别交y轴于点C1,C2,C3,连接OB1,OB2,OB3,则图中阴影部分的面积之和为_________.
中考数学填空题专项训练(二十九)
二、填空题(每小题3分,共21分)
9. 计算:=_______.
10. 一个函数具有下列性质:①它的图象不经过第三象限;②图象经过点(-1,1);③当x>-1时,函数值y随自变量x的增大而增大.试写出一个满足上述三条性质的函数的解析式____________________.
11. 在“五一”来临之际,小明一家人决定从人民公园、世纪欢乐园、海洋馆、动物园四处景点中选两处去旅游,则恰好选中世纪欢乐园、动物园两处景点的概率是_______.
12. 如图,扇形的圆心角∠AOB=135°,C为扇形弧上的一点,∠BOC=45°,设扇形BOC,△AOC,弓形AmC的面积分别为S1,S2,S3,则它们之间的大小关系是_________________.
第12题图 第13题图 第14题图
13. 如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边的中点,过D点作DE⊥DF,交AB于点E,交BC于点F,若AE=4,FC=3,则EF=______.
14. 已知:如图,双曲线(k<0,x>0)的图象经过Rt△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k=_______.
15. 将长方形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图1);再沿过点E的直线折叠,使点D落在BE边上的点D′处,折痕为EG(如图2);再展平纸片(如图3),则图3中tan∠α=_______.
中考数学填空题专项训练(三十)
二、填空题(每小题3分,共21分)
9. 分解因式:a4-16a2=_________.
10. “一根弹簧原长为10cm,在弹性限度内最多可挂质量为5kg的物体,挂上物体后弹簧伸长的长度与所挂物体的质量成正比,,则弹簧的总长度y(cm)与所挂物体质量x(kg)之间的函数关系式为y=10+0.5x(0≤x≤5).”王刚同学在阅读上面材料时发现部分内容被墨迹污染,被污染的部分是确定函数关系式的一个条件,你认为该条件可以是:_____________________.(只需写出1个)
11. 把一个体积是64立方厘米的立方体木块的表面涂上红漆,然后锯成体积为1立方厘米的小立方体,从中任取一块,则取出的这一块至少有一面涂红漆的概率是_________.
12. 如图,圆心角都为90°的扇形OAB与扇形OCD叠放在一起,OA=1,OC=3,将扇形OAB绕O点旋转一定的角度得到右图(0°<∠AOC<90°),分别连接AC,BD,则图中阴影部分的面积为__________.
第12题图 第13题图
13. 如图,直线与x轴交于点C,与y轴交于点D,以CD为边作矩形CDAB,点A在x轴上,双曲线(k<0,x>0)经过点B,与直线CD交于点E,EM⊥x轴于点M,则S四边形BEMC=__________.
14. 如图,在直线m上摆放着三个正三角形:△ABC,△HFG,△DCE,已知BC=CE,F,G分别是BC,CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S2,S3,若S1+S3=10,则S2=______.
15. 在□ABCD中,AB=6,AD=8,∠B是锐角,将△ACD沿对角线折叠,点D落在△ABC所在平面内的点E处,如果AE恰好经过BC的中点,则□ABCD的面积是______.
2014年中考数学填空题专项训练(一)答案
9. -4(答案不唯一) 10. 70° 11.1
查看更多