第二次统测数学试卷1

第二次统测数学试卷1

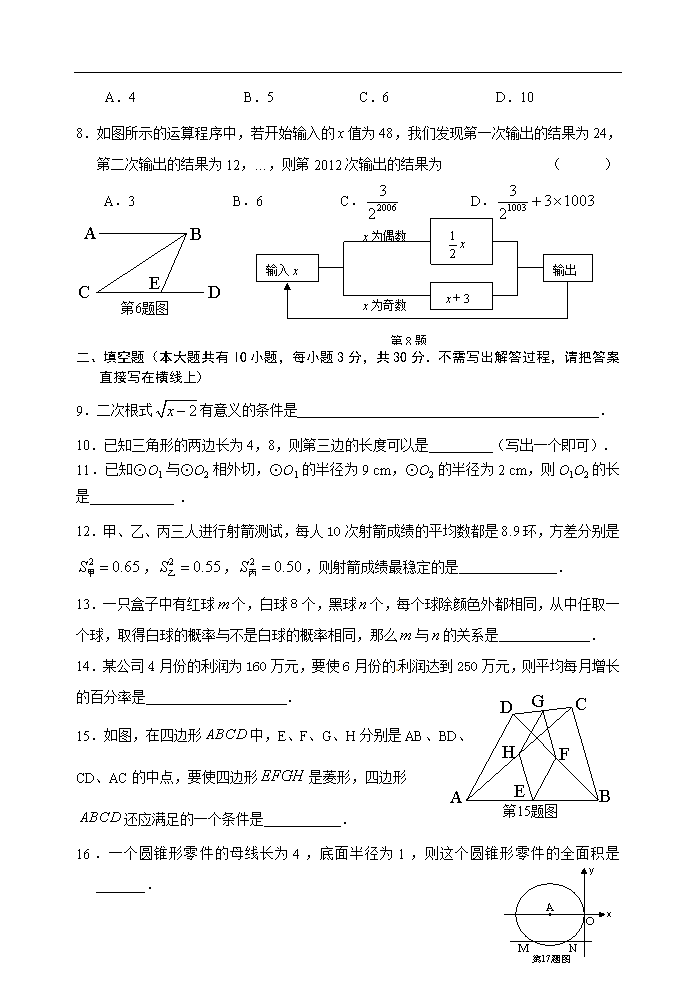
‎2011-2012学年度第二学期九年级第二次统测 考试时间：共120分钟 试卷满分150分 欢迎你参加第二次统测，祝你取得好成绩！‎ 温馨提示：本次考试分试卷和答题纸两部分，所有答案一律写在答题纸规定范围内，写在试卷上，答题无效。‎ 数 学 试 题 一、选择题(本大题共有8小题，每小题3分，共24分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填在括号内)‎ ‎1．下列各组数中，互为相反数的是 （ ）‎ A．2和－2 B．－2和 C．－2和－ D．和2‎ ‎2．据中新社北京2011年l‎2月8日电2011年中国粮食总产量达到546 400 000吨，用科学记数法表示为 （ ）‎ A．吨 B．吨 C．吨 D．吨 ‎3．下列四个几何体中，主视图是三角形的是 （ ） ‎ A．‎ B．‎ C．‎ D．‎ ‎4．下列运算正确的是 （ ）‎ A． B． C． D．‎ ‎5．设，在两个相邻整数之间，则这两个整数是 （ ）‎ A．1和2 B．2和3 C．3和4 D．4和5‎ ‎6．如图，已知AB∥CD，BC平分∠ABE，∠C＝34°，则∠BED的度数是 （ )‎ ‎ A． B． C． D．‎ ‎7．某车间5名工人日加工零件数分别为6，10，4，5，4，则这组数据的中位数是（ ）‎ A．4 B．5 C．6 D．10‎ ‎8．如图所示的运算程序中，若开始输入的x值为48，我们发现第一次输出的结果为24，第二次输出的结果为12，…，则第2012次输出的结果为 （ ）‎ 输出 输入x x＋3‎ x为偶数 x为奇数 第8题 A．3　　　 B．6　　 C．　　　　　D．‎ 二、填空题（本大题共有lO小题，每小题3分，共30分．不需写出解答过程，请把答案直接写在横线上)‎ ‎9．二次根式有意义的条件是 ．‎ ‎10．已知三角形的两边长为4，8，则第三边的长度可以是 （写出一个即可）.‎ ‎11．已知⊙O1与⊙O2相外切，⊙O1的半径为9 cm，⊙O2的半径为2 cm，则O1O2的长是 .‎ ‎12．甲、乙、丙三人进行射箭测试，每人10次射箭成绩的平均数都是环，方差分别是，，，则射箭成绩最稳定的是 ．‎ ‎13．一只盒子中有红球个，白球8个，黑球个，每个球除颜色外都相同，从中任取一个球，取得白球的概率与不是白球的概率相同，那么与的关系是 ．‎ ‎14．某公司4月份的利润为160万元，要使6月份的利润达到250万元，则平均每月增长的百分率是 ．‎ ‎15．如图，在四边形中，E、F、G、H分别是AB、BD、‎ CD、AC的中点，要使四边形是菱形，四边形 还应满足的一个条件是 ．‎ ‎16．一个圆锥形零件的母线长为4，底面半径为1，则这个圆锥形零件的全面积是_______．‎ ‎17．如图，在平面直角坐标系中，与轴相切于原点，‎ 平行于轴的直线交于、两点，若点的坐标 是，则弦M的长为 ．‎ ‎18．如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第（是大于0的整数）个图形需要黑色棋子的个数是 ．‎ 三、解答题（共96分）‎ ‎19．（本题满分8分）计算：‎ ‎20．（本题满分8分）先化简，然后从不等组的解集中，选取一个你认为符合题意的x的值代入求值．‎ ‎21．（本题8分) 如图，、是平行四边形对角线上的两点，∥．‎ 求证：．‎ ‎22．（本题满分9分）今年“五一”假期，某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点，再从B点沿斜坡BC到达山顶C点，路线如图所示.斜坡AB的长为1040米，斜坡BC的长为400米，在C点测得B点的俯角为30°,已知A点海拔121米，C点海拔721米.‎ ‎（1）求B点的海拔；‎ ‎（2）求斜坡AB的坡度．‎ ‎23．（本题满分8分）初中生对待学习的态度一直是教育工作者关注的问题之一．为此市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣），并将调查结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：‎ ‎（1）此次抽样调查中，共调查了 名学生；‎ ‎（2）将图①补充完整；‎ ‎（3）求出图②中C级所占的圆心角的度数；‎ ‎（4）根据抽样调查结果，请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标（达标包括A级和B级）？‎ 人数 ‎120‎ ‎100‎ ‎50‎ ‎50‎ ‎120‎ A级 B级 C级 学习态度层级 图①‎ 图②‎ ‎25%‎ A级 B级 C级 ‎60%‎ 图②‎ ‎ ‎ ‎24．（本题满分10分）甲、乙、丙、丁四位同学进行一次乒乓球单打比赛，要从中选出两位同学打第一场比赛，‎ ‎⑴请用树状图法或列表法，求恰好选中甲、乙两位同学的概率；‎ ‎⑵若已确定甲打第一场，再从其余三位同学中随机选取一位，求恰好选中乙同学的概率．‎ ‎25．（本题满分11分）如图，在平面直角坐标系xOy中，一次函数y＝kx＋b(k≠0)的图象与反比例函数y＝ (m≠0)的图象交于二、四象限内的A、B两点，与x轴交于C点，点B的坐标为(6，n)，线段OA＝5，E为x轴负半轴上一点，且sin∠AOE＝．‎ ‎(1)求该反比例函数和一次函数；‎ ‎(2)求△AOC的面积．‎ ‎26. （本题满分11分） 如图，已知二次函数的图象与坐标轴交于点A（-1， 0）和点B（0，-5）．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）已知该函数图象的对称轴上存在一点P，使得△ABP的周长最小．请求出点P的坐标．‎ x O A ‎（第26题图）‎ B y ‎27．（本题满分11分）我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定他们的大小，即要比较代数式M、N的大小，只要作出它们的差M－N，若M－N＞0，则M＞N；若M－N＝0，则M＝N；若M－N＜0，则M＜N．‎ a a a a b b b b 图1‎ 如图1，把边长为a＋b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，试比较两个小正方形面积之和M与两个矩形面积之和N的大小．‎ 解：由图可知：M＝a2＋b2，N＝2ab． ∴M－N＝a2＋b2－2ab＝(a－b)2．‎ ‎∵a≠b，∴(a－b)2＞0． ∴M－N＞0． ∴M＞N．‎ 类别应用 ‎(1)已知小丽和小颖购买同一种商品的平均价格分别为元/千克和 元/千克(a、b是正数，且a≠b)，试比较小丽和小颖所购买商品的平均价格的高低．‎ ‎(2)试比较图2和图3中两个矩形周长M1、N1的大小(b＞c)．‎ ‎(3)联系拓广：小刚在超市里买了一些物品，用一个长方体的箱子“打包”，这个箱子的尺寸如图4所示(其中b＞a＞c＞0)，售货员分别可按图5、图6、图7三种方法进行捆绑，问哪种方法用绳最短？哪种方法用绳最长？请说明理由．‎ ‎28．（本题满分12分）如图，已知 四边形OABC为直角梯形，A（4，0），B（3，4），C（0，4）． 点从 出发以每秒2个单位长度的速度向运动；点从同时出发，以每秒1个单位长度的速度向运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点作垂直轴于点，连结AC交NP于Q，连结MQ． ‎ ‎（1）点 （填M或N）能到达终点；‎ ‎（2）求△AQM的面积S与运动时间t的函数关系式，并写出自变量t的取值范围，当t为何值时，S的值最大；‎ ‎（3）是否存在点M，使得△AQM为直角三角形？若存在，求出点M的坐标，若不存在，说明理由．‎