【数学】宁夏中卫市2020届高三下学期高考第三次模拟考试试题（文）（解析版）

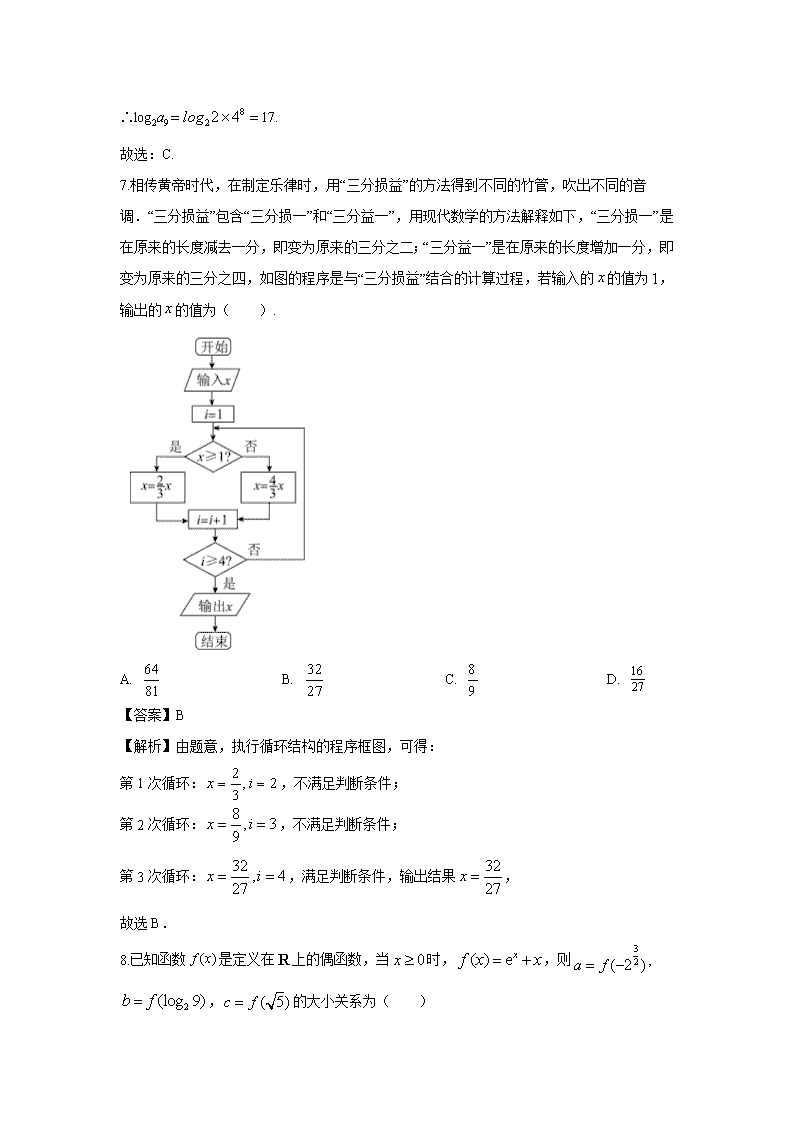
【数学】宁夏中卫市2020届高三下学期高考第三次模拟考试试题（文）（解析版）

宁夏中卫市2020届高三下学期高考第三次模拟考试 数学试题（文） ‎ 第Ⅰ卷 一、选择题（本大题共12个小题，每小题5分，共60分.每小题给出的选项中，只有一项是符合题目要求的）‎ ‎1.若复数z=，则|z|=（ ）‎ A. 1 B. C. 5 D. 5‎ ‎【答案】B ‎【解析】|z|===，‎ 故选：B.‎ ‎2.已知集合，，则（ ）‎ A. B. ‎ C. D. 或 ‎【答案】C ‎【解析】由题,因为,则,即,所以,‎ 所以,‎ 故选:C.‎ ‎3.已知、为实数，则是的（ ）条件 A. 充分不必要 B. 必要不充分 C. 充要条件 D. 不充分也不必要 ‎【答案】A ‎【解析】由得，此时成立，‎ 由，此时当、有负数时，不成立，‎ 即“”是“”的充分不必要条件，‎ 故选：A.‎ ‎4.已知数列，，，…，是首项为1，公差为2得等差数列，则等于( )‎ A. 9 B. ‎5 ‎C. 4 D. 2‎ ‎【答案】A ‎【解析】‎ 故选：A.‎ ‎5.某学校为落实学生掌握社会主义核心价值观的情况，用系统抽样的方法从全校2400名学生中抽取30人进行调查.现将2400名学生随机地从1～2400编号，按编号顺序平均分成30组（1～80号，81～160号，…，2321～2400号），若第3组与第4组抽出的号码之和为432，则第6组抽到的号码是（ ）‎ A. 416 B. ‎432 ‎C. 448 D. 464‎ ‎【答案】A ‎【解析】设第组抽到的号码是，则构成以80为公差的等差数列，‎ 所以，，‎ 所以，解得，‎ 所以.‎ 故选A.‎ ‎6.已知数列{an}是各项均为正数的等比数列，a1＝2，a3＝‎2a2+16，则log‎2a9＝（ ）‎ A. 15 B. ‎16 ‎C. 17 D. 18‎ ‎【答案】C ‎【解析】∵数列{an}是各项均为正数的等比数列，a1＝2，a3＝‎2a2+16，‎ ‎∴2q2＝2×2q+16，且q＞0，‎ 解得q＝4，‎ ‎∴log‎2a917.‎ 故选：C.‎ ‎7.相传黄帝时代，在制定乐律时，用“三分损益”的方法得到不同的竹管，吹出不同的音调．“三分损益”包含“三分损一”和“三分益一”，用现代数学的方法解释如下，“三分损一”是在原来的长度减去一分，即变为原来的三分之二；“三分益一”是在原来的长度增加一分，即变为原来的三分之四，如图的程序是与“三分损益”结合的计算过程，若输入的的值为，输出的的值为（ ）.‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】由题意，执行循环结构的程序框图，可得：‎ 第1次循环：，不满足判断条件；‎ 第2次循环：，不满足判断条件；‎ 第3次循环：，满足判断条件，输出结果，‎ 故选B．‎ ‎8.已知函数是定义在上的偶函数，当时，，则,，的大小关系为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】依题意得，，‎ 当时，，因为，所以在上单调递增，又在上单调递增，所以在上单调递增，‎ ‎，即，‎ 故选：C.‎ ‎9.已知菱形的边长为2，为的中点，，则的值为（ ）‎ A. 4 B. ‎-3 ‎C. D. ‎ ‎【答案】B ‎【解析】菱形的边长为2，，‎ ‎∴，‎ ‎∵为的中点，‎ ‎∴，，‎ ‎∴ ．‎ 故选B．‎ ‎10.已知实数，满足约束条件，则的最小值是（ ）‎ A. B. C. D. 1‎ ‎【答案】B ‎【解析】由约束条件作出可行域，‎ 是由， ，三点所围成的三角形及其内部，‎ 如图中阴影部分，‎ 而可理解为可行域内的点到原点距离的平方，‎ 显然原点到所在的直线的距离是可行域内的点到原点距离的最小值，‎ 此时，‎ 故选：B.‎ ‎11.已知双曲线的左、右焦点分别为，点在双曲线的右支上，点为的中点，为坐标原点，，则该双曲线的离心率为（ ）‎ A. B. ‎2 ‎C. D. ‎ ‎【答案】C ‎【解析】双曲线左、右焦点分别为，为坐标原点，‎ 由为的中点，所以，且，‎ ‎，故，即，‎ 设双曲线的焦距为‎2c，双曲线中满足 所以，化简可得 故双曲线的离心率为.‎ 故选:C.‎ ‎12.函数的定义域为，其导函数为，，且为偶函数，则（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】由于为偶函数，所以函数关于对称.由于，所以当时，递减，当时，，递增.所以.‎ 故选：A.‎ Ⅱ卷（非选择题共90分）‎ 二、填空题：（本大题共4小题，每小题5分，共20分）‎ ‎13.已知l，m是平面外的两条不同直线．给出下列三个论断：‎ ‎①l⊥m；②m∥；③l⊥．‎ 以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．‎ ‎【答案】如果l⊥α，m∥α，则l⊥m或如果l⊥α，l⊥m，则m∥α.‎ ‎【解析】将所给论断，分别作为条件、结论，得到如下三个命题：‎ ‎（1）如果l⊥α，m∥α，则l⊥m. 正确；‎ ‎（2）如果l⊥α，l⊥m，则m∥α.正确；‎ ‎（3）如果l⊥m，m∥α，则l⊥α.不正确，有可能l与α斜交、l∥α.‎ ‎14.已知函数，则不等式的解集为 .‎ ‎【答案】.‎ ‎【解析】若，则，‎ 若：则，故不等式的解集是.‎ ‎15.已知，，，均为锐角，则___________‎ ‎【答案】‎ ‎【解析】由于都是锐角，所以，‎ 所以，，‎ 所以 ‎．‎ 故答案：.‎ ‎16.已知椭圆，作倾斜角为的直线交椭圆C于A、B两点，线段的中点M，O为坐标原点，与的夹角为，且，则____________‎ ‎【答案】‎ ‎【解析】设，‎ 则，，‎ 两式相减，得．‎ 两点直线的倾斜角为，，‎ ‎，即，‎ 设直线的倾斜角为，则或 所以，因为，‎ 所以，解得，即 故答案为：.‎ 三、解答题：（本大题共6小题，满分70分，解答须写出文字说明，证明过程或演算步骤）‎ ‎17.设的内角A，B，C的对边分别为a，b，c，已知，且.‎ ‎（1）求角C的大小；‎ ‎（2）若向量与共线，求的周长.‎ 解：（1）因为，所以 所以，所以 所以，所以 因为是的内角，所以 ‎（2）因为向量与共线 所以，即 由余弦定理可得，即 解得 所以的周长为 ‎18.如图，四棱锥的底面是平行四边形，是等边三角形且边长是4，.‎ ‎（1）证明：；‎ ‎（2）若，求四棱锥的体积.‎ 证明：取AP中点M，连接DM，BM，‎ ‎，，‎ ‎，，‎ ‎，平面DMB．‎ 又平面DMB，‎ 解：由知，平面BDM，‎ 在等边三角形PAB中，由边长为4，得，‎ 在等腰三角形ADP中，由，，得，‎ 又，，得．‎ ‎．‎ 则．‎ ‎．‎ ‎19.2019年双十一落下帷幕，天猫交易额定格在268（单位：十亿元）人民币（下同），再创新高，比去年218（十亿元）多了50（十亿元）．这些数字的背后，除了是消费者买买买的表现，更是购物车里中国新消费的奇迹，为了研究历年销售额的变化趋势，一机构统计了2010年到2019年天猫双十一的销售额数据y（单位：十亿元），绘制如表：‎ 年份 ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎2018‎ ‎2019‎ 编号x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 销售额y ‎0.9‎ ‎8.7‎ ‎22.4‎ ‎41‎ ‎65‎ ‎94‎ ‎132.5‎ ‎172.5‎ ‎218‎ ‎268‎ 根据以上数据绘制散点图，如图所示 ‎（1）根据散点图判断，与哪一个适宜作为销售额关于的回归方程类型？（给出判断即可，不必说明理由）‎ ‎（2）根据（1）的判断结果及如表中的数据，建立关于的回归方程，并预测2020年天猫双十一销售额；（注：数据保留小数点后一位）‎ ‎（3）把销售超过100（十亿元）的年份叫“畅销年”，把销售额超过200（十亿元）的年份叫“狂欢年”，从2010年到2019年这十年的“畅销年”中任取2个，求至少取到一个“狂欢年”的概率．‎ 参考数据：‎ 参考公式：‎ 对于一组数据，其回归直线的斜率和截距的最小二乘估计公式分别，．‎ 解：（1）由散点图可知，适宜作为销售额关于的回归方程类型；‎ ‎（2）令，则．，‎ ‎，‎ ‎，则关于的回归方程为，取，得（十亿元）．‎ 预测2020年天猫双十一销售额为324.7（十亿元）；‎ ‎（3）2010年到2019年这十年中“畅销年”有4年，其中“狂欢年”有2年．‎ 从中任取2个，基本事件总数为共6个 至少取到一个“狂欢年”的事件数为共5个 则至少取到一个“狂欢年”的概率为．‎ ‎20.已知抛物线：的焦点为，点为抛物线上一点，且点到焦点的距离为4，过作抛物线的切线（斜率不为0），切点为.‎ ‎（Ⅰ）求抛物线的标准方程；‎ ‎（Ⅱ）求证：以为直径的圆过点.‎ ‎（1）解：由题知，，‎ ‎∴，解得，‎ ‎∴抛物线的标准方程为.‎ ‎（Ⅱ）证明：设切线的方程为，，‎ 联立，消去可得，‎ 由题意得，即，‎ ‎∴切点，‎ 又，∴.‎ ‎∴，故以为直径的圆过点.‎ ‎21.已知函数（，），.‎ ‎（Ⅰ）讨论的单调性；‎ ‎（Ⅱ）若对任意的，恒成立，求实数的取值范围.‎ 解：（Ⅰ）（），‎ 当时，在单调递减，在单调递增；‎ 当时，在单调递增，在单调递减.‎ ‎（Ⅱ）（），即，（）.‎ 令（），‎ 则，‎ 令，，故在单调递增，‎ 注意到，，‎ 于是存在使得，‎ 可知在单调递增，在单调递减.‎ ‎∴.‎ 综上知，.‎ 选考题：（请考生在第22、23两道题中任选一题作答.如果多做，则按所做的第一题记分.作答时请用2B铅笔在答题卡上把所选题目的题号涂黑）‎ 选修4-4：坐标系与参数方程 ‎22.在直角坐标系中，曲线的参数方程为（为参数，将曲线经过伸缩变换后得到曲线.在以原点为极点，轴正半轴为极轴的极坐标系中，直线的极坐标方程为.‎ ‎（1）说明曲线是哪一种曲线，并将曲线的方程化为极坐标方程；‎ ‎（2）已知点是曲线上的任意一点，又直线上有两点和，且，又点的极角为，点的极角为锐角.求：‎ ‎①点的极角；‎ ‎②面积的取值范围.‎ 解：（1）因为曲线的参数方程为（为参数），‎ 因为则曲线的参数方程 所以的普通方程为.所以曲线为圆心在原点，半径为2的圆.‎ 所以的极坐标方程为，即.‎ ‎（2）①点的极角为，代入直线的极坐标方程得点 极径为，且，所以为等腰三角形，‎ 又直线的普通方程为，‎ 又点的极角为锐角，所以，所以，‎ 所以点的极角为.‎ ‎②解法1：直线的普通方程为.‎ 曲线上的点到直线的距离 ‎.‎ 当，即（）时，‎ 取到最小值为.‎ 当，即（）时，‎ 取到最大值为.‎ 所以面积的最大值为；‎ 所以面积的最小值为；‎ 故面积取值范围.‎ 解法2：直线的普通方程为.‎ 因为圆的半径为2，且圆心到直线的距离，‎ 因，所以圆与直线相离.‎ 所以圆上的点到直线的距离最大值为，‎ 最小值为.‎ 所以面积的最大值为；‎ 所以面积的最小值为；‎ 故面积的取值范围.‎ 选修4—5：不等式选讲 ‎23.已知函数，且．‎ ‎（1）若，求的最小值，并求此时的值；‎ ‎（2）若，求证:．‎ 解：（1），‎ 法一:，，‎ 的最小值为，此时；‎ 法二:，‎ ‎，即的最小值为，此时；‎ 法三：由柯西不等式得：‎ ‎，‎ ‎,即的最小值为，此时；‎ ‎（2），，‎ 又，‎ ‎.‎