中考一轮复习教案之图形及其变换（四）15-17

中考一轮复习教案之图形及其变换（四）15-17

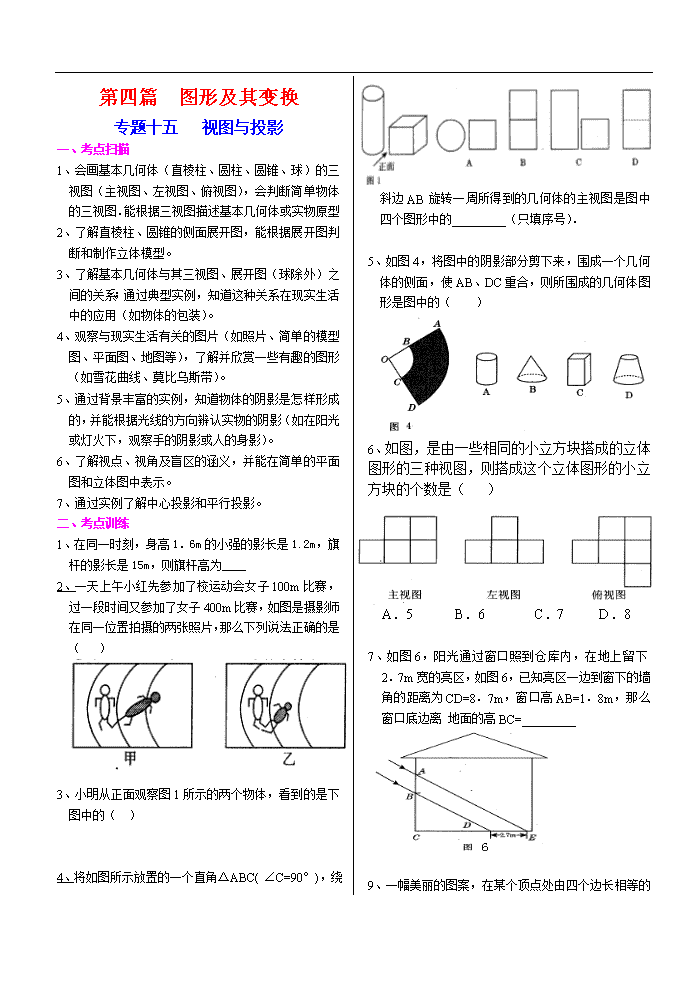
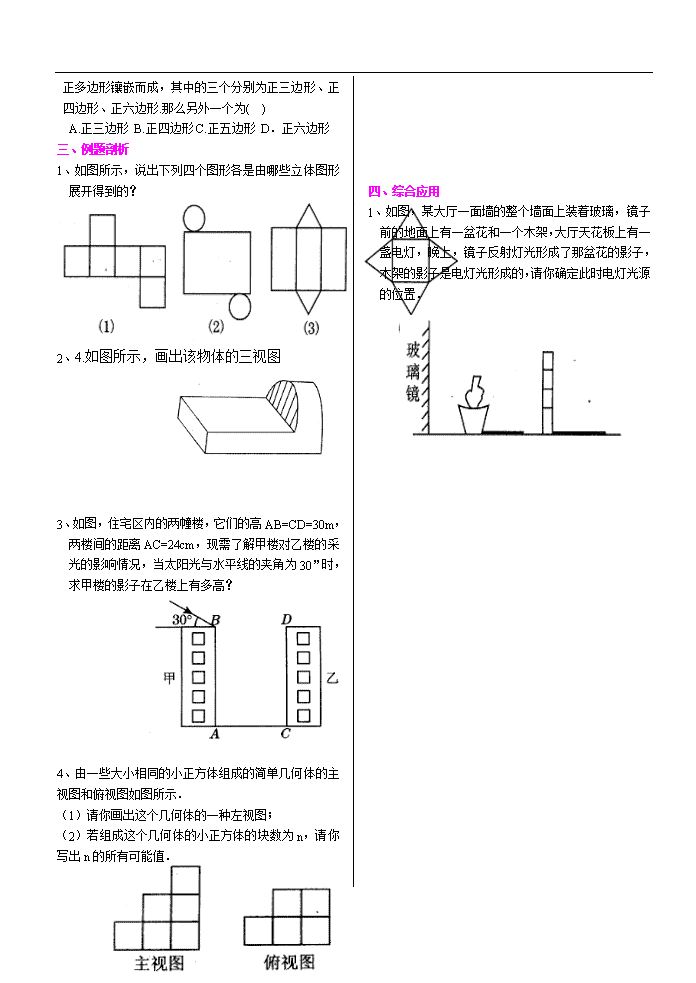
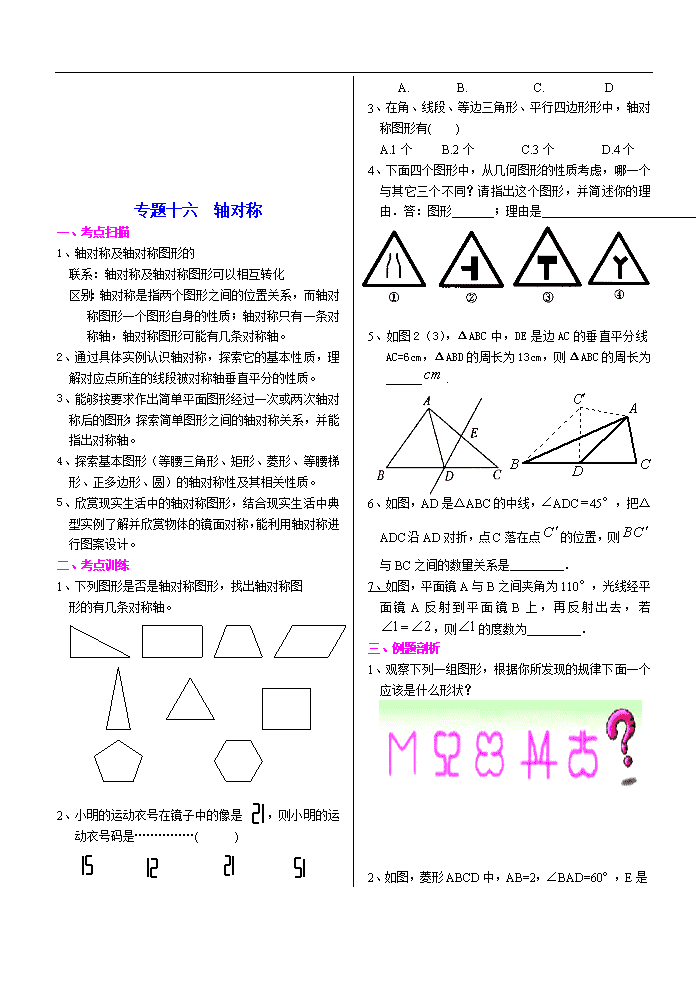
第四篇 图形及其变换 专题十五 视图与投影 一、考点扫描 ‎1、会画基本几何体（直棱柱、圆柱、圆锥、球）的三视图（主视图、左视图、俯视图），会判断简单物体的三视图．能根据三视图描述基本几何体或实物原型 ‎2、了解直棱柱、圆锥的侧面展开图，能根据展开图判断和制作立体模型。‎ ‎3、了解基本几何体与其三视图、展开图（球除外）之间的关系；通过典型实例，知道这种关系在现实生活中的应用（如物体的包装）。‎ ‎4、观察与现实生活有关的图片（如照片、简单的模型图、平面图、地图等），了解并欣赏一些有趣的图形（如雪花曲线、莫比乌斯带）。‎ ‎5、通过背景丰富的实例，知道物体的阴影是怎样形成的，并能根据光线的方向辨认实物的阴影（如在阳光或灯火下，观察手的阴影或人的身影）。‎ ‎6、了解视点、视角及盲区的涵义，并能在简单的平面图和立体图中表示。‎ ‎7、通过实例了解中心投影和平行投影。‎ 二、考点训练 ‎1、在同一时刻，身高1．‎6m的小强的影长是‎1.2m，旗杆的影长是‎15m，则旗杆高为 ‎ ‎2、一天上午小红先参加了校运动会女子‎100m比赛，过一段时间又参加了女子‎400m比赛，如图是摄影师在同一位置拍摄的两张照片，那么下列说法正确的是（ ）‎ ‎3、小明从正面观察图1所示的两个物体，看到的是下图中的（ ）‎ ‎4、将如图所示放置的一个直角△ABC( ∠C=90°)，绕斜边AB旋转一周所得到的几何体的主视图是图中四个图形中的_________（只填序号）．‎ ‎5、如图4，将图中的阴影部分剪下来，围成一个几何体的侧面，使AB、DC重合，则所围成的几何体图形是图中的（ ）‎ ‎6、如图，是由一些相同的小立方块搭成的立体图形的三种视图，则搭成这个立体图形的小立方块的个数是（ ）‎ ‎ A．5 B．‎6 C．7 D．8‎ ‎7、如图6，阳光通过窗口照到仓库内，在地上留下2．‎7m宽的亮区，如图6，已知亮区一边到窗下的墙角的距离为CD=8．‎7m，窗口高AB=1．‎8m，那么窗口底边离 地面的高BC=_________‎ ‎9、‎ 一幅美丽的图案，在某个顶点处由四个边长相等的正多边形镶嵌而成，其中的三个分别为正三边形、正四边形、正六边形.那么另外一个为( )‎ ‎ A.正三边形 B.正四边形C.正五边形 D．正六边形 三、例题剖析 ‎1、如图所示，说出下列四个图形各是由哪些立体图形展开得到的？‎ ‎2、4.如图所示，画出该物体的三视图 ‎　　　　　　　　　　　　　　　　　　　　　　‎ ‎3、如图，住宅区内的两幢楼，它们的高AB=CD=‎30m，两楼间的距离AC=‎24cm，现需了解甲楼对乙楼的采光的影响情况，当太阳光与水平线的夹角为‎30”‎时，求甲楼的影子在乙楼上有多高？‎ ‎4、由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图所示．‎ ‎（1）请你画出这个几何体的一种左视图；‎ ‎（2）若组成这个几何体的小正方体的块数为n，请你写出n的所有可能值．‎ 四、综合应用 ‎1、如图，某大厅一面墙的整个墙面上装着玻璃，镜子前的地面上有一盆花和一个木架，大厅天花板上有一盏电灯，晚上，镜子反射灯光形成了那盆花的影子，木架的影子是电灯光形成的，请你确定此时电灯光源的位置．‎ 专题十六 轴对称 一、考点扫描 ‎1、轴对称及轴对称图形的 联系：轴对称及轴对称图形可以相互转化 区别：轴对称是指两个图形之间的位置关系，而轴对称图形一个图形自身的性质；轴对称只有一条对称轴，轴对称图形可能有几条对称轴。‎ ‎2、通过具体实例认识轴对称，探索它的基本性质，理解对应点所连的线段被对称轴垂直平分的性质。‎ ‎3、能够按要求作出简单平面图形经过一次或两次轴对称后的图形；探索简单图形之间的轴对称关系，并能指出对称轴。‎ ‎4、探索基本图形（等腰三角形、矩形、菱形、等腰梯形、正多边形、圆）的轴对称性及其相关性质。‎ ‎5、欣赏现实生活中的轴对称图形，结合现实生活中典型实例了解并欣赏物体的镜面对称，能利用轴对称进行图案设计。‎ 二、考点训练 ‎1、下列图形是否是轴对称图形，找出轴对称图 形的有几条对称轴。‎ ‎2、小明的运动衣号在镜子中的像是 ，则小明的运动衣号码是……………( )‎ A. B. C. D ‎3、在角、线段、等边三角形、平行四边形形中，轴对称图形有( )‎ A.1个 B.2个 C.3个 D.4个 ‎4、下面四个图形中，从几何图形的性质考虑，哪一个与其它三个不同？请指出这个图形，并简述你的理由．答：图形 ；理由是 ：‎ ‎5、如图2（3），ΔABC中，DE是边AC的垂直平分线AC=‎6cm，ΔABD的周长为‎13cm，则ΔABC的周长为______.‎ ‎6、如图，AD是△ABC的中线，∠ADC＝45°，把△ADC沿AD对折，点C落在点的位置，则与BC之间的数量关系是 ．‎ ‎7、如图，平面镜A与B之间夹角为110°，光线经平面镜A反射到平面镜B上，再反射出去，若，则的度数为 ．‎ 三、例题剖析 ‎ ‎1、观察下列一组图形，根据你所发现的规律下面一个应该是什么形状？‎ ‎2、如图，菱形ABCD中，AB=2，∠BAD=60°，E是 AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是　　　 ．‎ ‎3、如图，P在∠AOB内，点M、N分别是点P关于AO、BO的对称点，MN分别交OA、OB于E、F.‎ ‎⑴若△PEF的周长是20cm，求MN的长. ‎ ‎⑵若∠AOB=30°试判断△MNO的形状，并说明理由 ‎4、将一张长方形的纸对折，如图5所示可得到一条折痕（图中虚线）．续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么对折四次可以得到 条折痕．如果对折n次，可以得到 条折痕．‎ 四、综合应用 ‎1、做一做:‎ 用四块如图1的瓷砖拼成一个正方形,使拼成的图案成轴对称图形.请你在图2、图3、图4中各画出一种拼法（要求三种拼法各不相同，所画图案中的阴影部分用斜线表示）.‎ ‎2、（05福州）已知如图，在直角梯形ABCD中，AD∥BC，‎ ‎ BC=‎5cm，CD=‎6cm，∠DCB=60º，∠ ABC=90º，等边三角形MNP（N为不动点）的边长为a cm，边MN和直角梯形ABCD的底边BC都在直线l上，NC=‎8 cm ,将直角梯形ABCD向左翻折180º，翻折一次得图形①，翻折二次得图形②，如此翻折下去。‎ ‎(1)、将直角梯形ABCD向左翻折二次，如果此时等边三角形MNP的边长a≥‎2cm，这时两图形重叠部分的面积是多少？‎ ‎(2)、将直角梯形ABCD向左翻折三次，如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积就等于直角梯形ABCD的面积，这时等边三角形MNP的边长a至少应为多少？‎ ‎(3)、将直角梯形ABCD向左翻折三次，如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积的一半，这时等边三角形MNP的边长a应为多少？‎ A B P M N ‎②‎ ‎①‎ D C 专题十七 平移与旋转 一、考点扫描 ‎1、图形的平移 ‎①通过具体实例认识平移，探索它的基本性质，理解对应点连线平行且相等的性质。‎ ‎②能按要求作出简单平面图形平移后的图形。‎ ‎③利用平移进行图案设计，认识和欣赏平移在现实生活中的应用。‎ ‎2、图形的旋转 ‎①通过具体实例认识旋转，探索它的基本性质，理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质。‎ ‎②了解平行四边形、圆是中心对称图形。中心对称的概念和性质。‎ ‎③能够按要求作出简单平面图形旋转后的图形。‎ ‎④欣赏旋转在现实生活中的应用。‎ ‎⑤探索图形之间的变换关系（轴对称、平移、旋转及其组合）。‎ ‎⑥灵活运用轴对称、平移和旋转的组合进行图案设计。‎ 二、考点训练 ‎1、下列说法正确的是（ ）‎ A．旋转后的图形的位置一定改变 ‎ ‎ B．旋转后的图形的位置一定不变 C．旋转后的图形的位置可能不变 ‎ ‎ D．旋转后的图形的位置和形状都发生变化 ‎2、下列关于旋转和平移的说法错误的是（ ）‎ A．旋转需旋转中心和旋转角，而平移需平移方向和平移距离 B．旋转和平移都只能改变图形的位置 C．旋转和平移图形的形状和大小都不发生变化 D．旋转和平移的定义是相同的 ‎3、在“党”“在”“我”“心”“中”五个汉字中，旋转180o后不变的字是_____，在字母“X”、“V”、“Z”、“H”中绕某点旋转不超过180后能与原图形重合的是____。‎ ‎4、△ABC是等腰直角三角形，如图，A B=A C，∠BA C＝90°，D是BC上一点，△ACD经过旋转到达△ABE的位置，则其旋转角的 度数为（ ）‎ A．90° B．120° C．60° D．45°‎ ‎5、有以下图形：平行四边形、矩形、等腰三角形、线段、圆、菱形，其中既是轴对称图形又是中心对称图形的有（ ）‎ ‎ A．4个 B．5个 C．6个 D．3个 ‎6、如图2的图案中，可以看出由图案自身的部分经过平移而得到的是（ ） ‎ ‎ 图2‎ ‎7、有以下现象：①温度计中，液柱的上升或下降；②打气筒打气时，活塞的运动；③钟摆的摆动；④传送带上瓶装饮料的移动，其中属于平移的是（ ）‎ ‎ A、①③ B、①② C、②③ D、②④‎ ‎8、如图1，若将△ABC绕点C顺时针旋转90°后得到 ‎△，则A点的对应点A′的坐标是（ ）‎ A、（－3，－2）B、（2，2） C、（3，0）D、（2，1）‎ 三、例题剖析 ‎1、如图，在△ABC中，∠C=90°，AC=‎2cm，把这个三角形在平面内绕点C顺时针旋转90°，那么点A移动所走过的路线长是 cm．(不取近似值)‎ ‎2、将两块含30°角且大小相同的直角三角板如图3摆放。‎ ‎(1)将图3中△绕点C顺时针旋转45°得图4，点与AB的交点，求证：；‎ ‎(2)将图4中△绕点C顺时针旋转30°到△（如图5），点与AB的交点。线段之间存在一个确定的等量关系，请你写出这个关系式并说明理由；‎ 图3 图4‎ 图5‎ 图6‎ ‎（3）将图5中线段绕点C顺时针旋转60°到 （如图6），连结，求证：⊥AB.‎ 四、综合应用 ‎1、把两个全等的等腰直角三角板ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针方向旋转（旋转角α满足条件：0°＜α＜90°)，四边形CHGK是旋转过程中两三角板的重叠部分（如图②）.‎ ‎(1)在上述旋转过程中，BH与CK有怎样的数量关系？四边形CHGK的面积有何变化？证明你发现的结论；‎ ‎(2)连接HK，在上述旋转过程中，设BH=，△GKH的面积为，求与之间的函数关系式，并写出自变量的取值范围；‎ ‎(3)在(2)的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的？若存在，求出此时的值；若不存在，说明理由.‎ A G(O)‎ E C B F ‎①‎