甘肃省高三第一次高考诊断考试月文科数学试卷 word
2016 年甘肃省第一次高考诊断考试
文科数学
第 I 卷 (选择题,共 60 分) 2016.3.17
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只
有一项是
符合题目要求的.
1.已知集合 A={0,1},B={ -1,0,a+2},且 A B,则实数 a=
A.0 B.-1 C.-2 D.-3
2.复数 z= (i 为虚数单位)在复平面内对应点的坐标是
A.(1,4) B.(4,-1) C.(4,1) D.(- 1,4)
3.设 p:l
1,则 P 是 q 成立的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.下列函数中,既是偶函数又存在零点的是
A.y=x2 +1 B.y=2|x| C.y= lnx D.y=cosx
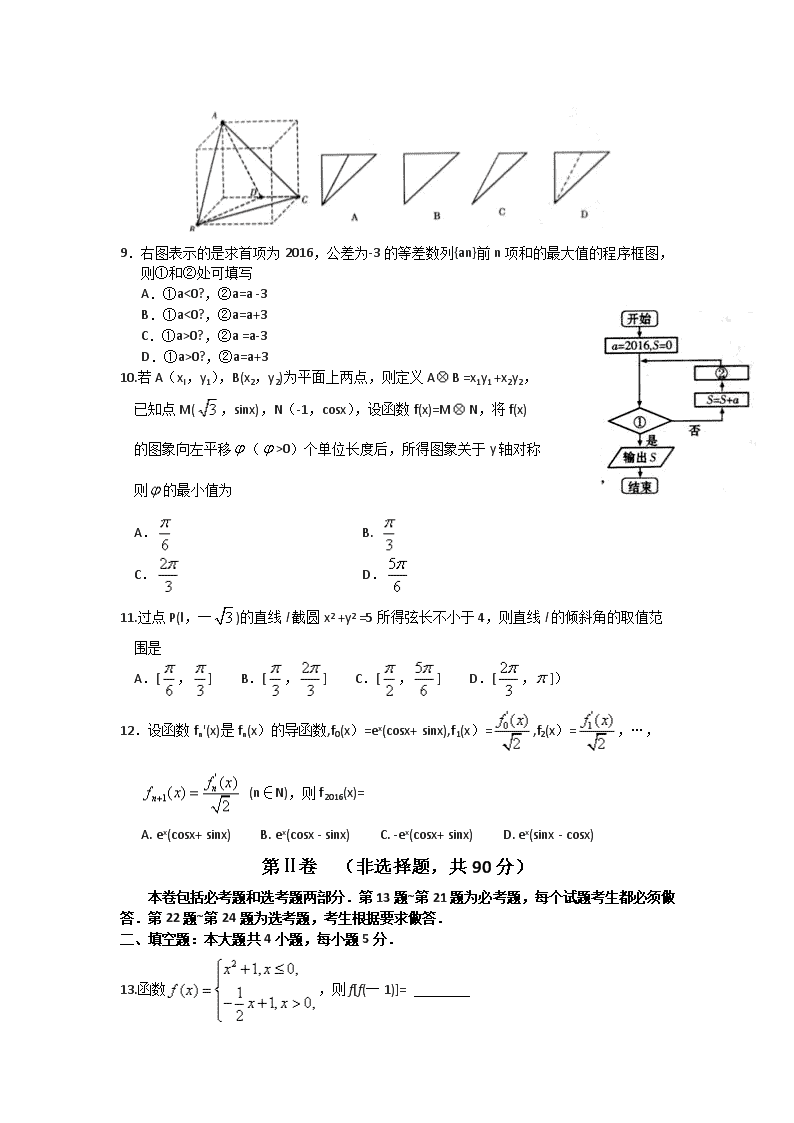
5.为了了解学生参加体育锻炼的情况,现抽取了 n 名学
生进行调查,结果显示这些学生每月的锻炼时间(单
位:小时)都在[10,50],其中锻炼时间在[30,50]的学
生有 134 人,频率分布直方图如图所示,则 n=
A.150 B.160
C.180 D.200
6.若变量 x,y,满足约束条件 ,且 z=x+y 的
最大值和最小值分别为 m 和 n.则
m -n =
A.5 B.6 C.7 D.8
7.设非零向量 a,b,c 满足|a|=|b|=|c|,a+b= c,则向量 a 与向量 c 的夹角为
A. 150° B.120° C.60° D.30°
8.如图三棱锥 A - BCD,则该三棱锥的俯视图是
9.右图表示的是求首项为 2016,公差为-3 的等差数列{an}前 n 项和的最大值的程序框图,
则①和②处可填写
A.①a<0?,②a=a -3
B.①a<0?,②a=a+3
C.①a>0?,②a =a-3
D.①a>0?,②a=a+3
10.若 A(xl,y1),B(x2,y2)为平面上两点,则定义 A B =x1y1 +x2y2,
已知点 M( ,sinx),N(-1,cosx),设函数 f(x)=M N,将 f(x)
的图象向左平移 ( >0)个单位长度后,所得图象关于 y 轴对称
则 的最小值为
A. B.
C. D.
11.过点 P(l,一 )的直线 l 截圆 x2 +y2 =5 所得弦长不小于 4,则直线 l 的倾斜角的取值范
围是
A.[ , ] B.[ , ] C.[ , ] D.[ , ])
12.设函数 fn'(x)是 fn(x)的导函数,f0(x)=ex(cosx+ sinx),f1(x)= ,f2(x)= ,…,
(n∈N),则 f2016(x)=
A. ex(cosx+ sinx) B. ex(cosx - sinx) C. -ex(cosx+ sinx) D. ex(sinx - cosx)
第Ⅱ卷 (非选择题,共 90 分)
本卷包括必考题和选考题两部分.第 13 题~第 21 题为必考题,每个试题考生都必须做
答.第 22 题~第 24 题为选考题,考生根据要求做答.
二、填空题:本大题共 4 小题,每小题 5 分.
13.函数 ,则 f[f(一 1)]=
14.已知α,β∈(0,π),cosa= ,cos(α十β)= ,则 cosβ= .
15.已知双曲线 =l(a>0,b>0)的一条渐近线与直线 2x+y 一 3=0 垂直,则该双曲
线
的离心率为_______.
16.已知正四面体 ABCD 的棱长为 l,E 是 AB 的中点,过 E 作其外接球的截面,则此截面面积
的最小值为______.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分 12 分)
在等差数列{an}中,公差 d≠0,a1=2,a1,a3,a7 成等比数列.
(I)求数列{an}的通项公式 an;
(Ⅱ)设 bn= ,求数列{bn}的前 n 项和 Sn.
18.(本小题满分 12 分)
如图,在三棱锥 P - ABC 中,E、F、G、H 分别是棱 PB、PC、
AB、BC 的中点,PA⊥平面 ABC,AB⊥ AC.PA =AB =AC =2.
( I)证明:FG⊥AH;
(Ⅱ)求三棱锥 E - FGH 的体积,
19.(本小题满分 12 分)
某期《我是歌手》中有 7 位歌手(1 至 7 号)参加比赛,由 500
名大众评审现场投票决定歌手名次.根据年龄将大众评审分为五组,各组的人数如下:
组别 A B C D E
人数 50 100 150 150 50
( I)为了调查大众评审对 7 位歌手的支持状况,现用分层抽样方法从各组中抽取若干评
审,其中从 B 组抽取了 6 人,请将其余各组抽取的人数填入下表;
组别 A B C D E
人数 50 100 150 150 50
抽取人数 6
(Ⅱ)在(I)中,若 A,B 两组被抽到的评审中各有 2 人支持 7 号歌手,现从这两组被抽到
的评审中分别任选 1 人,求这 2 人都支持 7 号歌手的概率.
20.(本小题满分 12 分)
已知 F1,F2 为椭圆 =l(a>b>0)的左、右焦点,B1,B2 椭圆短轴的端点,四边形
F1B1,F2B2 为正方形且面积等于 50.
(I)求椭圆方程;
(Ⅱ)过焦点 Fl 且倾斜角为 30°的直线 l 交椭圆于 M,N 两点,求△F2MN 内切圆的半径.
21.(本小题满分 12 分)
设函数 f(x)=(a +b)ex,g(x)=一 x2+cx+d.若函数 f(x)和 g(x)的图象都过点 P(0,1),
且在点 P 处有相同的切线 y= 2x +1.
(I)求 a,b,c,d 的值;
(Ⅱ)当 x [0,+∞)时,判断函数 h(x)=f(x)一 g(x)的单调性.
请考生在第 22、23、24 三题中任选一题做答,如果多做,则按所做的第一题记分.
22.(本小题满分 10 分)选修 4-1:几何证明选讲
如图所示,AB 为圆 D 的直径,BC 为圆 O 的切线,过 A 作 OC
的平行线交圆 O 于 D,BD 与 OC 相交于 E.
(I)求证:CD 为圆 O 的切线;
(Ⅱ)若 OA =AD =4,求 OC 的长.
23.(本小题满分 10 分)选修 4-4:坐标系与参数方程
已知在直角坐标系 xOy 中,曲线 C 的方程是(x-2)2 +(y-l)2 =4,直线 l 经过点 P(3, ),
倾斜角为 ,以 O 为极点,x 轴的正半轴为极轴建立极坐标系.
(I)写出曲线 C 的极坐标方程和直线 Z 的参数方程;
(II)设直线 l 与曲线 C 相交于 A,B 两点,求|OA|·|OB|的值
24.(本小题满分 10 分)选修 4-5:不等式选讲
设函数 f(x)= |x - a|(a∈R).
(I)当 a=3 时,解不等式 f(x)≥4 - |x +l|;
(Ⅱ)若不等式 f(x)≤l 的解集为[1,3],且 (m>0,n>0),求 m+2n 的最小值,