百校联考2020年高考考前冲刺必刷卷(三) 数学(文)
百校联考2020年高考考前冲刺必刷卷(三)
文科数学
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
2.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置。
3.全部答案写在答题卡上,写在本试卷上无效。
4.本试卷满分150分,测试时间120分钟。
5.考试范围:必修1,必修4,必修5第1章,选修1-1第1章,第3章。
第I卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x|x2+2x=0},B={x|2|x-1|=2},则A∪B=
A.{0} B.{0,2} C.{0,-2} D.{-2,0,2}
2.已知A(-1,2),B(2,-1),若点C满足,则点C坐标为
A.(,) B.(-3,3) C.(3,-3) D.(-4,5)
3.已知命题p:对x∈(-∞,0),x2019
0)的图象的相邻两个交点的距离为2π,若f(x)在(-m,m)(m>0)上是增函数,则m的取值范围是
A.(0,] B.(0,] C.(0,] D.(0,]
7.已知定义在R上的奇函数f(x)满足f(x)+f(2-x)=0,则下列结论错误的是
A.f(x)的图象关于点(1,0)对称 B.f(x+2)=f(x)
C.f(3-x)=f(x-1) D.f(x-2)=f(x)
8.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,用现代式子表示即为:在△ABC中,角A,B,C所对的边分别为a,b,c,则△ABC的面积S=。根据此公式,若acosB+(b+3c)cosA=0,且a2-b2-c2=2,则△ABC的面积为
A. B.2 C. D.2
9.已知单位向量a,b满足|a-b|=,若a-c,b-c共线,则|c|的最小值为
A. B.1 C. D.
10.已知a=,b=ln,c满足2c=,则下列关系正确的是
A.a>b>c B.c>a>b C.a>c>b D.b>c>a
11.已知函数f(x)=sin(ωx+φ)(ω>0),若存在实数a,使得f(a)=f(a+1)=-,且f(x)在(a,a+1)上有最小值,没有最大值,则f(x)在(0,2019)上的零点个数最少为
A.1344 B.1345 C.1346 D.1347
12.设[x]表示不超过x的最大整数,若f(x)=ex-lnx的最小值为M,则[M]=
A.-1 B.0 C.1 D.2
第II卷
二、填空题:本大题共4小题,每小题5分。
13.若,且f(a)=2,则a= 。
14.tan67.5°-tan22.5°= 。
15.如图所示的平面直角坐标系中,网格小正方形的边长为1,若向量a,b,c满足c=xa+yb,且(ka-b)·c=0,则= 。
16.在△ABC中,角A,B,C所对的边分别为a,b,c,若bcosC=2ccosB,且c=2,则△ABC面积的最大值为 。
三、解答题:解答应写出文字说明,证明过程和解题步骤。
17.(本小题满分10分)
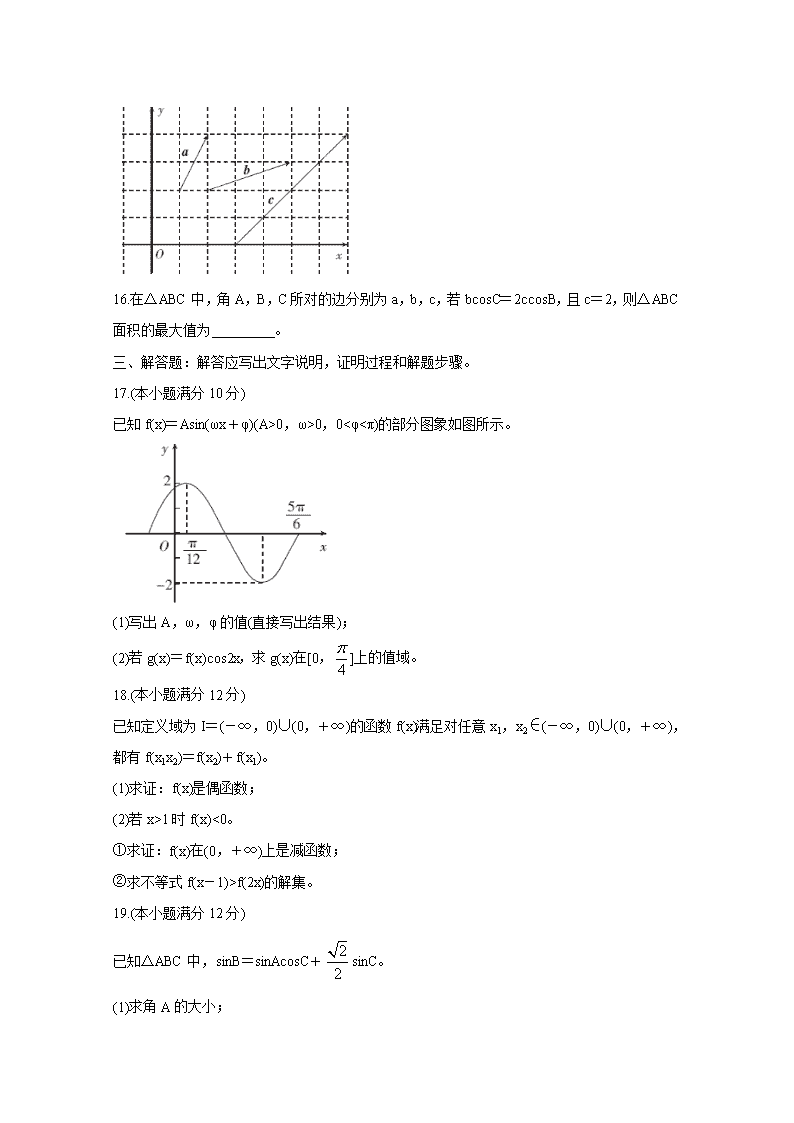
已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示。
(1)写出A,ω,φ的值(直接写出结果);
(2)若g(x)=f(x)cos2x,求g(x)在[0,]上的值域。
18.(本小题满分12分)
已知定义域为I=(-∞,0)∪(0,+∞)的函数f(x)满足对任意x1,x2∈(-∞,0)∪(0,+∞),都有f(x1x2)=f(x2)+f(x1)。
(1)求证:f(x)是偶函数;
(2)若x>1时f(x)<0。
①求证:f(x)在(0,+∞)上是减函数;
②求不等式f(x-1)>f(2x)的解集。
19.(本小题满分12分)
已知△ABC中,sinB=sinAcosC+sinC。
(1)求角A的大小;
(2)若AB=2AC,点D在边BC上,且BD=2DC,AD=,求AB。
20.(本小题满分12分)
已知函数f(x)=2a(x+1)ex-(x2+4x)。
(1)讨论f(x)的单调性;
(2)若x>-2时f(x)>2,求实数a的取值范围。
21.(本小题满分12分)
中国共产党十六届五中全会提出要按照“生产发展、生活富裕、乡风文明、村容整洁、管理民主”的要求,扎实推进社会主义新农村建设,2018年4月习近平近日作出重要指示强调,要结合实施农村人居环境整治三年行动计划和乡村振兴战略,建设好生态宜居的美丽乡村。为推进新农村建设某自然村计划在村边一块废弃的五边形荒地上设置一个绿化区,如图所示,边界AB,BC,CD,DE,EA以及对角线BE均为绿化区小路(不考虑宽度),∠BCD=∠CDE=∠BAE=120°,BC=CD=100m,DE=400m。
(1)求四边形BCDE的面积;
(2)求绿化区所有小路长度之和的最大值。
22.(本小题满分12分)
已知函数f(x)=lnx-ax2+(1-2a)x(a∈R)。
(1)求f(x)的极值;
(2)若a=-1,正数m,n满足f(m)+f(n)=(m+2)(n+2),求证:m+n>2。