苏教版数学九年级上册教案2-2圆的对称性（2）

苏教版数学九年级上册教案2-2圆的对称性（2）

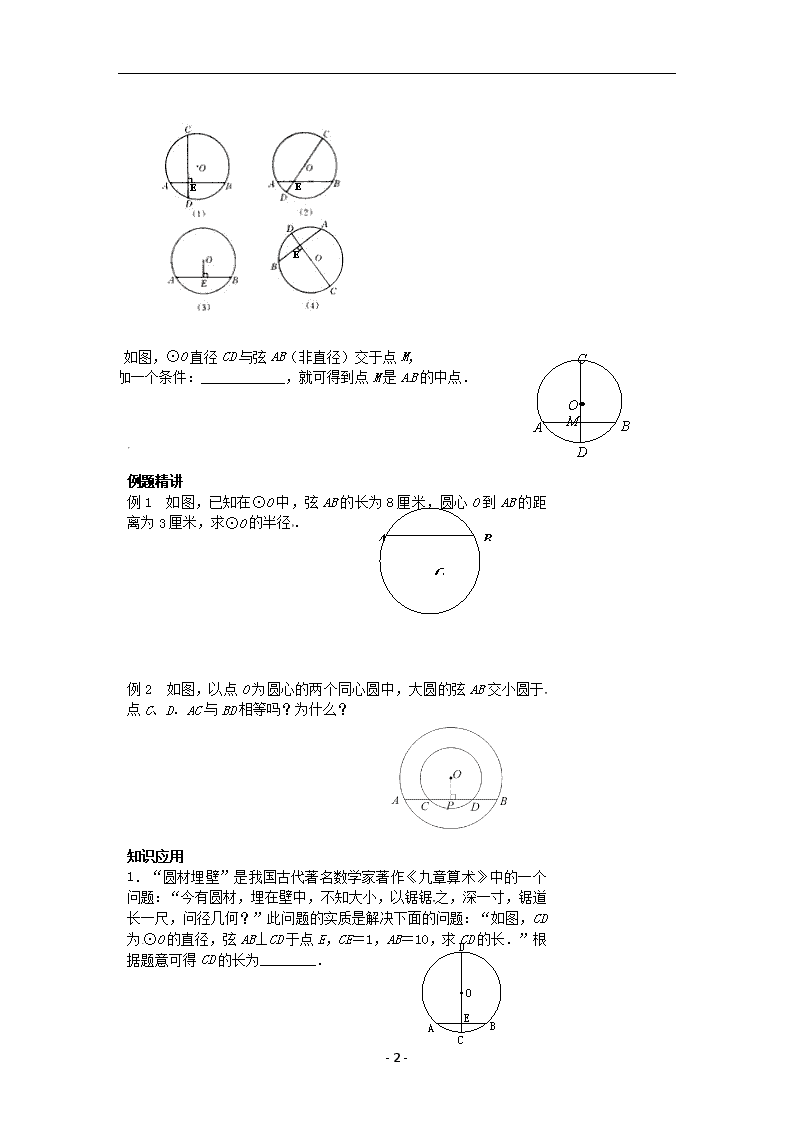
- 1 - 2.2 圆的对称性（2） 教学目标 【知识与能力】 会利用圆的轴对称性探究垂径定理、证明垂径定理. 【过程与方法】 能利用垂径定理进行相关的计算和证明 【情感态度价值观】 在经历探索与证明垂径定 理 的过程中，进一步体会和理解研究几何图形的各种方法，明白 圆的问题依旧要化归为直线形问题解决. 教学重难点 【教学重点】 垂径定理的证明及其简单应用. 【教学难点】 垂径定理的证明. 课前准备 无 教学过程 情境引入 圆是什么对称图形？你是如何验证的？ 实践探索一 圆的轴对称性． 1．圆是轴对称图形吗？如果是，它的对称轴是什么？你能找到多少 条对称轴？你是如何验证的？ 2．如何确定圆形纸片的圆心？动手试一试！ 实践探索二 垂径定理． 1．操作、探索 学生拿出事先准备好的透明的纸片，在上面画一个圆 O，再任意画一 条非直径的弦 CD，作一直径 AB 与 CD 垂直，交点为 P（如图 1）．沿 着直径将圆对折（如图 2），你有什么发现？ 图 1 图 2 2．请你用文字语言概括你对垂直于弦的直 径的研究过程中发现的结 论，其中条件和结论分别是什么？请用几何语言表示． 3．请证明你的发现． 定理巩固训练 1．下列图形中，哪些能使用垂 径定理，为什么？ - 2 - 2．如图，⊙O 直径 CD 与弦 AB（非直径）交于点 M， 添加一个条件：____________，就可得到点 M 是 AB 的中点． 例题精讲 例 1 如图，已知在⊙O 中，弦 AB 的长为 8 厘米，圆心 O 到 AB 的距 离为 3 厘米，求⊙O 的半径． 例 2 如图，以点 O 为圆心的两个同心圆中，大圆的弦 AB 交小圆于点 C、D．AC 与 BD 相等吗？为什么？ 知识应用 1．“圆材埋壁”是我国古代著名数学家著作《九章算术》中的一个 问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道 长一尺，问径几何？”此问题的实质是解决下面的问题：“如图，CD 为⊙O 的直径，弦 AB⊥CD 于点 E，CE＝1，AB＝10，求 CD 的长．”根 据题意可得 CD 的长为________． · A M D O B C . A B O B A C E D O - 3 - 1． 已知⊙O 的直径 50cm，弦 AB∥CD，且 AB＝40cm，CD＝48cm， 求 AB、CD 之间的距离． 拓展延伸 如图，AB、CD 是⊙O 的两条弦，AB∥CD，⌒AC 与⌒BD 相 等吗？为什么？ 小结与反思 通过本节课的学习，你对圆的对称性有哪些认识？