黑龙江省哈尔滨市第一中学2020届高三6月第一次模拟数学（文）试题

黑龙江省哈尔滨市第一中学2020届高三6月第一次模拟数学（文）试题

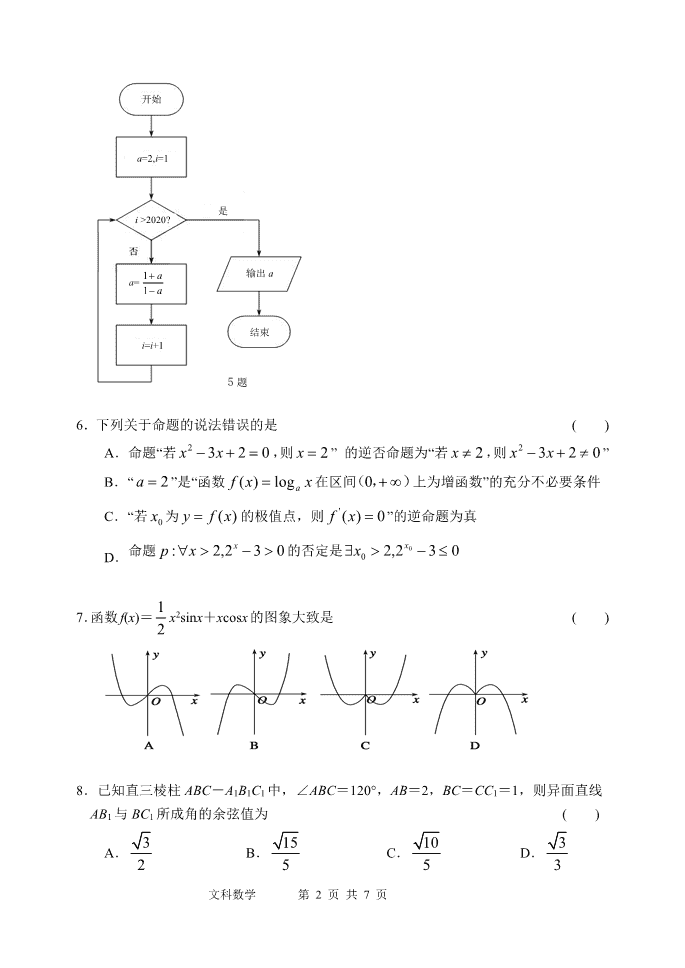
文科数学 第 1 页 共 7 页 哈尔滨市第一中学 2020 届高三学年六月第一次模拟考试 数 学（文史类） 第Ⅰ卷 （选择题，共 60 分） 考生须知： 1.本试卷分试题卷和答题卡，满分 150 分，考试时间 120 分钟。 2.答题前，在答题卡指定位置上填写学校、姓名和准考证号。 3.所有答案必须写在答题卡上，写在试卷上无效。 4.考试结束，只需上交答题卡。 一、选择题：（本大题共 12 个小题，每小题 5 分，共 60 分，在每个小题的四 个答案中，只有一项是符合题目要求的） 1．已知集合    02,3,2,1 2  mxxxBA ，若  2BA ，则集合 B ( ) A． 0 B． 2 C．  1 D． 20， 2．已知i 是虚数单位，则   i i 1 34 ( ) A． i55 B． i55 C． i2 5 2 5  D． i2 5 2 5  3．已知等比数列{ }na 满足 1 2a  ，且 1 2, ,6a a 成等差数列，则 4a  ( ) A． 6 B．8 C．16 D． 32 4．已知向量 a＝(1，m)，向量 b＝(3，－2)，且(a＋b)⊥b，则 m＝ ( ) A．－8 B．－6 C．6 D．8 5．执行如下图所示的程序框图，则输出的 a 值为 ( ) A．-3 B． 1 3 C． 2 1 D．2 文科数学 第 2 页 共 7 页 6．下列关于命题的说法错误的是 ( ) A．命题“若 0232  xx ，则 2x ” 的逆否命题为“若 2x ，则 0232  xx ” B．“ 2a ”是“函数 xxf alog)(  在区间 ），（ 0 上为增函数”的充分不必要条件 C．“若 0x 为 )(xfy  的极值点，则 0)(' xf ”的逆命题为真 D．命题 032,2:  xxp 的否定是 032,2 0 0  xx 7．函数f(x)＝ 1 2 x2sinx＋xcosx的图象大致是 ( ) 8．已知直三棱柱 ABC－A1B1C1 中，∠ABC＝120°，AB＝2，BC＝CC1＝1，则异面直线 AB1 与 BC1 所成角的余弦值为 ( ) A． 3 2 B． 15 5 C． 10 5 D． 3 3 5 题 开始 a=2,i=1 i >2020? 是 结束 输出 a i=i+1 a= 1 1 a a   文科数学 第 3 页 共 7 页 9．中国古代近似计算方法源远流长，早在八世纪，我国著名数学家、天文学家张隧（法 号：一行）为编制《大衍历》发明了一种近似计算的方法——二次插值算法（又称一 行算法，牛顿也创造了此算法，但是比我国张隧晚了上千年）：对于函数 ( )y f x ， 若  1 1 ,y f x  2 2 ,y f x  3 3 ,y f x 1 2 3x x x  ，则在区间 1 3,x x 上 ( )f x 可以 用二次函数     1 1 1 2 1 2( )f x y k x x k x x x x      来近似代替，其中 2 1 1 2 1 ,y yk x x   3 2 3 2 y yk x x   ， 1 2 3 1 k kk x x   ，若令 1 0,x 2 ,2x  3x  ，请依据上述 算法，估算 2sin 5  的近似值是 （ ） A． 24 25 B． 17 25 C． 16 25 D． 4 5 10．已知 )1( xf 是定义在 R 上的奇函数， 2)2( f ，且对任意 11 x ， 12 x ， 21 xx  ， 0)()( 21 21   xx xfxf 恒成立，则使不等式 2)log2( 2  xf 成立的 x 的取值范 围是 ( ) A． )1,0( B． )2,0( C．  ,4 D． )4,1( 11．已知 P 为抛物线 2 4y x 上一个动点，Q 为圆  22 4 1x y   上一个动点，则点 P 到 点 Q 的 距 离 与 点 P 到 抛 物 线 的 准 线 的 距 离 之 和 最 小 值 是 ( ) A． 17 1 B． 2 5 2 C． 2 D． 17 12．已知方程 0)3( 23  xxax 有 4 个不同的实数根，则实数 a 的取值范围是( ) A． ），（  9 4 B． ），（  3 2 C． ），（ 0 D． ），（  2 1 文科数学 第 4 页 共 7 页 第Ⅱ卷（非选择题，共 90 分） 二．填空题：（本大题共 4 个小题，每小题 5 分，共 20 分。把答案填写在答 题纸相应位置上） 13．为了了解疫情期间哈一中高三学生的心理需求，更好的开展高考前的心理健康教育 工作，心理老师设计了两个问题，第一个问题是“你出生的月份是奇数吗？”；第二个 问题是“你是否需要心理疏导？”。让被调查者在保密的情况下掷一个均匀的骰子，其 他人不知道掷骰子的结果，要求：当出现 1 点或 2 点时，回答第一个问题；否则回答 第二个问题，由于其他人不知道他回答的是哪一个问题，因此，当他回答“是”时， 你也无法知道他是否有心理问题，这种调查既保护了他的隐私，也能反映真实情况， 可以从调查结果中得到需要的估计，若调查的 900 名学生中有 156 人回答“是”，由此 可估计我校高三需要心理疏导的学生所占的比例约为_________________ 14．将函数 )0)(3sin(2)(  xxf 的图象向右平移 3   个单位，得到函数 y＝g(x) 的图象，若 y＝g(x)在     40 ， 上为增函数，则ω的最大值为________． 15．若圆 9)1(3 22  yx ）（ 与双曲线 )0,0(12 2 2 2  bab y a x 经过第二、四象限 的渐近线交于 BA, 两点，且 62AB ，则此双曲线的离心率为________． 16．某几何体的三视图如图所示，正视图为等腰三角形，俯视图为等腰梯形，则该几何 体外接球的表面积是________． 16 题 文科数学 第 5 页 共 7 页 三．解答题:（本大题共 6 个小题，共 70 分.解答应写出文字说明，证明过程 或演算步骤.） 17．(本小题满分 12 分)在△ABC 中，AD 是 BC 边的中线，AB2＋AC2＋AB·AC＝BC2，且 △ABC 的面积为 3 . (1)求∠BAC 的大小及AB→·AC→的值； (2)若 AB＝4，求 AD 的长． 18．(本小题满分 12 分)某种植园在芒果临近成熟时，随机从一些芒果树上摘下 100 个芒 果，其质量分别在[100,150)，[150,200)，[200,250)，[250,300)，[300,350)，[350,400)(单 位：克)中，经统计得频率分布直方图如图所示． (1)经计算估计这组数据的中位数； (2)某经销商来收购芒果，以各组数据的中间数代表这组数据的平均值，用样本估计 总体，该种植园中还未摘下的芒果大约还有 10000 个，经销商提出如下两种收购方案： A：所有芒果以 10 元/千克收购； B：对质量低于 250 克的芒果以 2 元/个收购，高于或等于 250 克的以 3 元/个收购． 通过计算确定种植园选择哪种方案获利更多？ 文科数学 第 6 页 共 7 页 19．（本小题满分 12 分）如图，正方形 ADMN 与矩形 ABCD 所在平面互相垂直， 2 6AB AD  ，点 E 为线段 AB 上一点． （1）若点 E 是 AB 的中点，求证：BM∥平面 NDE； （2）若直线 EM 与平面 ABCD所成的线面角的大小为 π 6 ，求 CDMEADMNE VV  : ． 20．（本小题满分 12 分）已知椭圆 C： 2 2 2 2 1x y a b   (a>b>0)的离心率为 1 2 ，且过点 ）（ 2 3,1 ， 椭圆 C 的右顶点为 A，点 B 的坐标为 ）（ 0,2 1 . (1)求椭圆 C 的方程； (2)已知纵坐标不同的两点 P，Q 为椭圆 C 上的两个点，且 B，P，Q 三点共线， 线段 PQ 的中点为 R，求直线 AR 的斜率的取值范围． 21．（本小题满分 12 分）已知函数   2 lnf x ax bx x   ，a，b R ． （1）当 1a b  时，求曲线  y f x 在 1x  处的切线方程； （2）当 2 1b a  时，讨论函数  f x 的单调性； （3）当 1a  ， 3b  时，记函数  f x 的导函数  f x 的两个零点是 1x 和 2x  1 2x x ． 求证：    1 2 3 ln 24f x f x   ． EA B CD N M 文科数学 第 7 页 共 7 页 选考题：本题满分 10 分.请考生在第 22、23 题中任选一题作答.如果多做, 则按所做的第一题计分,作答时用 2B 铅笔在答题卡上把所选题目对应的题号 涂黑. 22．[选修 4—4:坐标系与参数方程] 在平面直角坐标系中，以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系， 已知曲线C 的极坐标方程为 ）（ 0cossin 2  aa  ，过点 ）（ 4,2 P 的直线l 的参数方程为         ty tx 2 24 2 22 （t 为参数），直线l 与曲线C 相交于 BA, 两点． （1）写出曲线C 的直角坐标方程和直线l 的普通方程； （2）若 2ABPBPA  ，求 a 的值． 23．[选修 4—5:不等式选讲] 已知 a>0，b>0，函数 f(x)＝|x＋a|＋|2x－b|的最小值为 1. (1)证明：2a＋b＝2； (2)若 a＋2b≥tab 恒成立，求实数 t 的最大值．