2019届二轮复习抛物线中的三角形面积问题学案（全国通用）

2019届二轮复习抛物线中的三角形面积问题学案（全国通用）

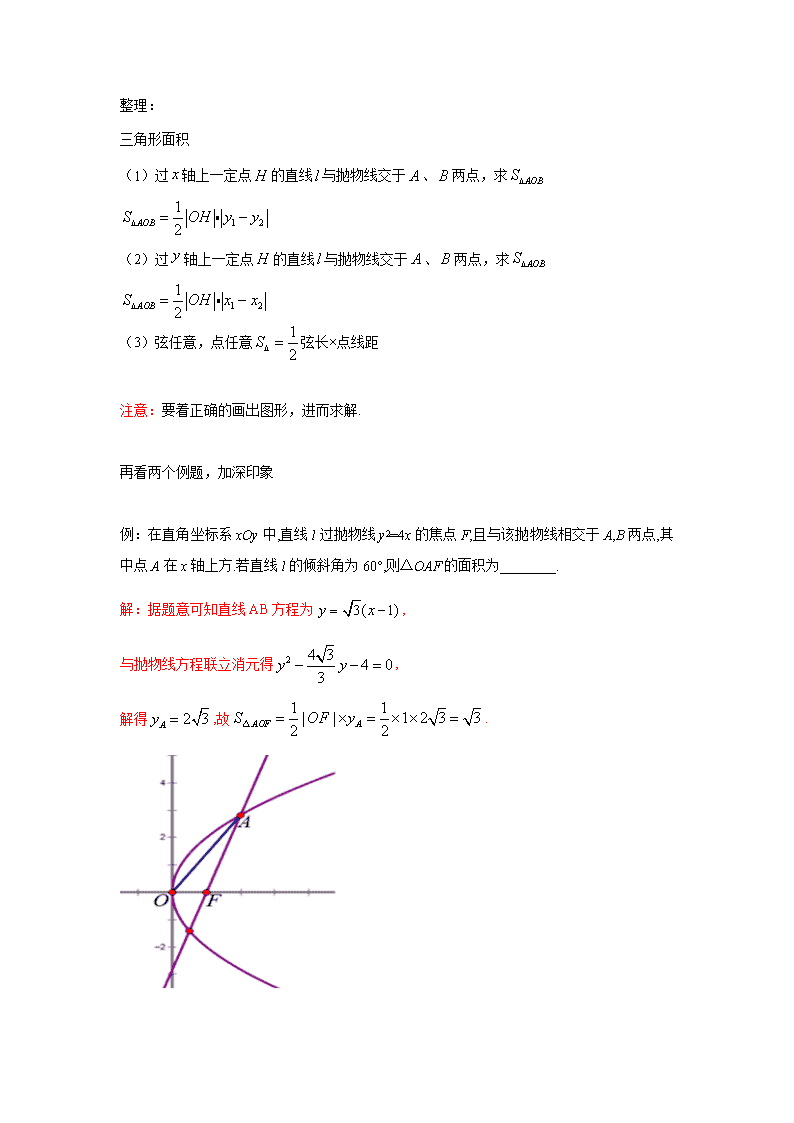
专题01 抛物线中的三角形面积问题 本内容主要研究抛物线中的面积问题.直线和抛物线相交，围成的平面图形种类很多，尤其以三角形最为常见，三角形面积的计算是重点，其他平面图形的面积可以转化为三角形面积的计算.直线和抛物线相交时联立方程，利用弦长公式，或者点线距公式，结合韦达定理解决问题.‎ 先看例题：‎ 例：已知直线l过抛物线C的焦点,且与C的对称轴垂直,l与C交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为( )‎ A.18‎ B.24‎ C.36‎ D.48‎ 整理：‎ 三角形面积 ‎（1）过轴上一定点的直线与抛物线交于、两点，求 ‎（2）过轴上一定点的直线与抛物线交于、两点，求 ‎（3）弦任意，点任意弦长×点线距 注意：要着正确的画出图形，进而求解.‎ 再看两个例题，加深印象 ‎ 例：在直角坐标系xOy中,直线l过抛物线y2=4x的焦点F,且与该抛物线相交于A,B两点,其中点A在x轴上方.若直线l的倾斜角为60°,则△OAF的面积为________.‎ ‎ ‎ 再看一个例题：‎ 例：已知抛物线y＝ax2－1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为________.‎ 解；本小题主要考查抛物线的方程及有关性质.‎ 总结：‎ ‎1.根据直线和抛物线的位置关系，如果弦任意，选择公式弦长×点线距.‎ ‎2.根据直线和抛物线的位置关系，如果直线过轴上一定点，设直线方程，代入抛物线方程计算弦长.‎ ‎3.根据直线和抛物线的位置关系，如果直线过轴上一定点，设直线方程，代入抛物线方程计算弦长.‎ 练习：‎ ‎1. O为坐标原点,F为抛物线C:的焦点,P为C上一点,若,则△POF的面积为( 　　)‎ A.2 B. C. D.4‎ ‎2. 连接抛物线x2=4y的焦点F与点M(1,0)所得的线段与抛物线交于点A,设点O为坐标原点,则三角形OAM的面积为( )‎ A. B. C. D. ‎ ‎3. 设斜率为2的直线l过抛物线y2=ax(a≠0)的焦点F,且和y轴交于点A.若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )‎ A.y2=±4x B.y2=±8x C.y2=4x D.y2=8x 答案：‎ ‎1.‎ ‎2.‎ ‎3.‎