- 2021-05-11 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
湖北省荆州三校2020届高三联考数学(文)试题
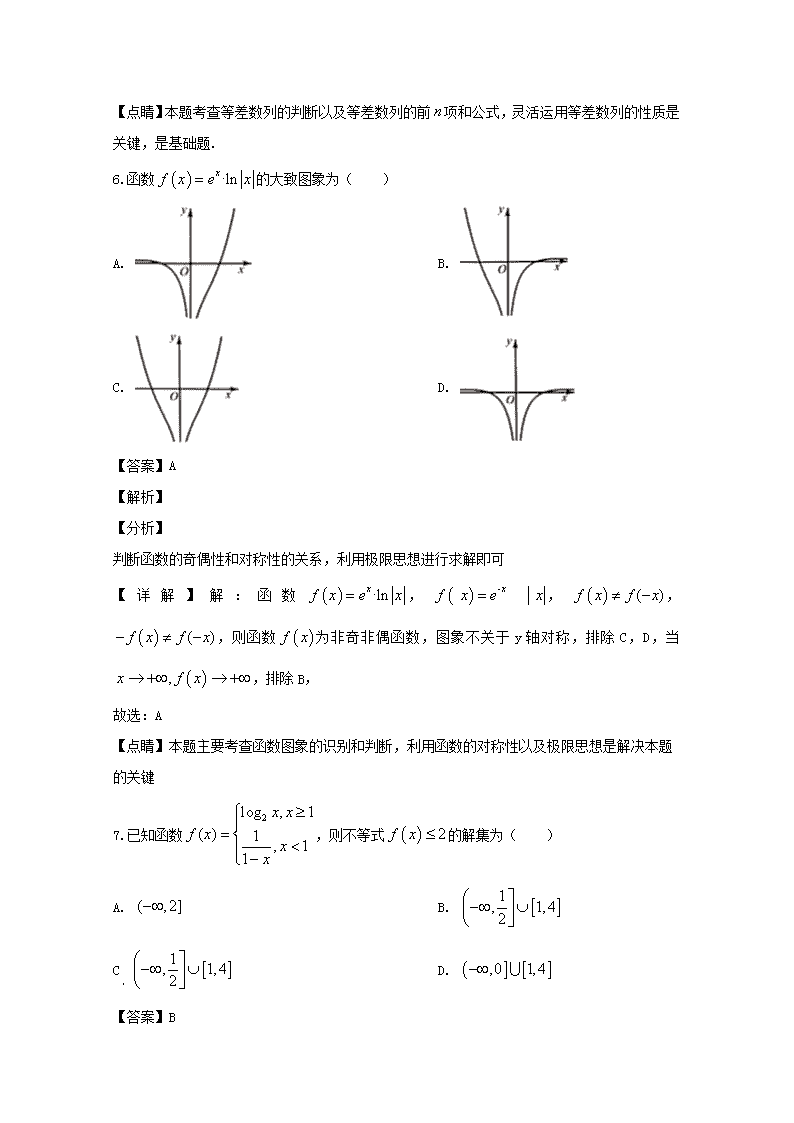
宜昌一中、荆州中学、龙泉中学三校联盟 高三11月联考 文科数学试题 一、选择题:(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。请将正确的答案填涂在答题卡上) 1.已知a为实数,若复数为纯虚数,则复数的虚部为( ) A. 3 B. 6 C. D. 6 【答案】D 【解析】 【分析】 根据复数为纯虚数,列方程求出的值,进而可得复数的虚部. 【详解】解:由已知,解得,故,其虚部为, 故选:D. 【点睛】本题考查复数的概念,注意纯虚数为实部为0,虚部不为0,是基础题. 2.已知,则( ) A. B. C. D. 【答案】B 【解析】 【分析】 求出集合中元素的具体范围,然后求交集即可. 【详解】解:, , , 故选:B. 【点睛】本题考查集合的交集运算,关键是要确定集合中的元素的范围,注意集合是求函数的定义域,不是值域,是基础题. 3.下列函数中,其定义域和值域与函数的定义域和值域相同的是( ) A. B. C. D. 【答案】C 【解析】 函数的定义域和值域均为,定义域值域都是,不合题意;函数的定义域为,值域为,不满足要求;函数的定义域为,值域为,不满足要求;函数的定义域和值域均为,满足要求,故选C. 4.三个数的大小顺序是 ( ) A. B. C. D. 【答案】D 【解析】 由题意得,,故选D. 5.数列满足,且,则( ) A. 95 B. 190 C. 380 D. 150 【答案】D 【解析】 【分析】 由条件可得数列是等差数列,利用等差数列的性质和前项和公式即可求. 【详解】解:,即为, 故数列等差数列, , 故选:D. 【点睛】本题考查等差数列的判断以及等差数列的前项和公式,灵活运用等差数列的性质是关键,是基础题. 6.函数的大致图象为( ) A. B. C. D. 【答案】A 【解析】 【分析】 判断函数的奇偶性和对称性的关系,利用极限思想进行求解即可 【详解】解:函数,,,,则函数为非奇非偶函数,图象不关于y轴对称,排除C,D,当,排除B, 故选:A 【点睛】本题主要考查函数图象的识别和判断,利用函数的对称性以及极限思想是解决本题的关键 7.已知函数,则不等式的解集为( ) A. B. C D. 【答案】B 【解析】 【分析】 分类讨论,分段解不等式,然后求并集. 【详解】解:当时,,解得; 当时,,解得, 综上所述不等式的解集为, 故选:B. 【点睛】本题考查分段函数不等式,注意每段中的范围,是基础题. 8.已知数列为等比数列,且,则( ) A. B. C. D. 【答案】B 【解析】 【详解】依题意,得,所以. 由,得,或(由于与同号,故舍去). 所以. . 故选A. 9.函数,则下列结论正确的是( ) A. 的最大值为1 B. 在上单调递增 C. 的图像关于直线对称 D. 的图像关于点对称 【答案】B 【解析】 【分析】 先将变形为的形式,然后根据三角函数的性质逐个判断选项的对错. 【详解】解:, 对A:,故A错误; 对B:令,解得, 因为Ü,故B正确; 对C:,1不是最值,故C错误; 对D:,的图像关于点对称,故D错误, 故选:B. 【点睛】本题考查函数的性质,是基础题. 10.下列判断正确的是( ) A. “”是“”的充分不必要条件 B. 命题“若则”的逆否命题为真 C. 命题“,”的否定是“,” D. 若命题p为真命题,命题q为假命题,则命题“”为真命题 【答案】D 【解析】 【分析】 对A利用任意角的三角函数的概念进行判断;对B直接就判断原命题的真假即可;对C利用全称命题的否定是特称命题,按照书写规律来判断;对D根据复合命题的真假规律来判断. 【详解】对A:当时,,但当时,不一定等于,则“”是“”的必要不充分条件,故A错; 对B:当时,若,则有,则命“题若则”是假命题,所以它的逆否命题也是假命题,故B错; 对C:命题“,”的否定是“,”,故C错; 对D:若命题p真命题,命题q为假命题,则命题为真命题,则命题“”为真命题,故D正确. 故选: D. 【点睛】本题考查充分性必要性的判断,互为逆否命题的真假判断,全称命题的否定以及复合命题的真假判断,是基础题. 11.已知函数在内不是单调函数,则实数的取值范围是( ) A. B. C. D. 【答案】A 【解析】 【分析】 求导f′(x)=2x,转化为f′(x)=2x在有变号零点,再分离参数求值域即可求解 【详解】∵f′(x)=2x,在内不是单调函数, 故2x在存在变号零点,即在存在有变号零点, ∴2查看更多
- 当前文档收益归属上传用户
- 下载本文档