- 2021-05-11 发布 |
- 37.5 KB |
- 20页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学上册第13章全等三角形13-5逆命题与逆定理第2课时线段垂直平分线作业课件新版华东师大版
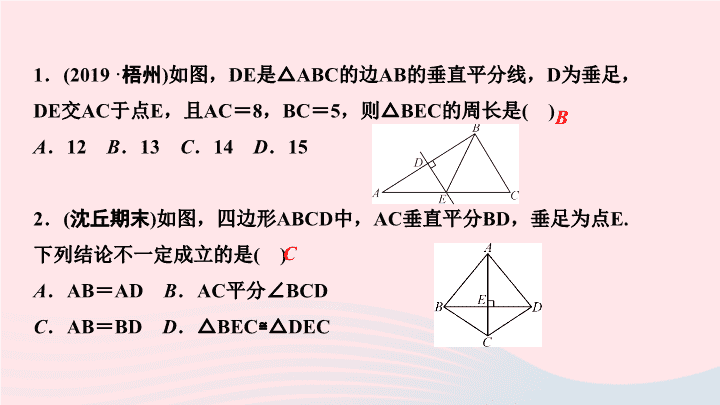
第13章 全等三角形 13.5 逆命题与逆定理 第2课时 线段垂直平分线 1 . (2019 · 梧州 ) 如图, DE 是△ ABC 的边 AB 的垂直平分线, D 为垂足, DE 交 AC 于点 E ,且 AC = 8 , BC = 5 ,则△ BEC 的周长是 ( ) A . 12 B . 13 C . 14 D . 15 2 . ( 沈丘期末 ) 如图,四边形 ABCD 中, AC 垂直平分 BD ,垂足为点 E. 下列结论不一定成立的是 ( ) A . AB = AD B . AC 平分∠ BCD C . AB = BD D .△ BEC≌△DEC B C 3 . ( 复习题 12 变式 ) 如图,已知 AB 比 AC 长 2 cm , BC 的垂直平分线 交 AB 于点 D ,交 BC 于点 E ,△ ACD 的周长是 14 cm ,求 AB 和 AC 的长. 解:∵ DE 垂直平分 BC ,∴ DB = DC. ∵AC + AD + DC = 14 cm ,∴ AC + AD + BD = 14 cm , 即 AC + AB = 14 cm . 又∵ AB - AC = 2 cm ,∴ AB = 8 cm , AC = 6 cm 4 .下列说法中错误的是 ( ) A .若直线 CD 为线段 AB 的垂直平分线,则 CA = CB , DA = DB B .若 CA = CB , DA = DB ,则直线 CD 垂直平分线段 AB C .若 CA = CB ,则点 C 在线段 AB 的垂直平分线上 D .若 DA = DB ,则经过点 D 的直线为线段 AB 的垂直平分线 D 5 .以线段 BC 为底边的等腰△ ABC 的顶点 A 在 ____________________ . 6 .如图, AC = AD , BC = BD , AB 与 CD 相交于点 O , 则 AB 与 CD 的关系是 ____________________ . 线段 BC 的垂直平分线上 AB 垂直平分 CD 7 . ( 习题 3 变式 ) 如图,在△ ABC 中, AC⊥BC , AD 平分∠ BAC , 交 BC 于点 D , DE⊥AB 于点 E. 求证:直线 AD 是 CE 的垂直平分线. 证明:易证△ ADE≌△ADC ,∴ AE = AC , DE = DC , ∴点 A , D 均在线段 CE 的垂直平分线上. 又∵两点确定一条直线,∴直线 AD 是 CE 的垂直平分线 8 .平面内到三角形三个顶点距离相等的点是 ( ) A .三角形三条角平分线的交点 B .三角形的三条中线的交点 C .三角形三边垂直平分线的交点 D .三角形三条高线的交点 C 9 . ( 海南中考 ) 已知△ ABC 的三边长分别为 4 , 4 , 6 , 在△ ABC 所在平面内画一条直线,将△ ABC 分割成两个三角形, 使其中的一个是等腰三角形,则这样的直线最多可画 ( ) A . 3 条 B . 4 条 C . 5 条 D . 6 条 B 10 . ( 南充中考 ) 如图,在△ ABC 中, AF 平分∠ BAC , AC 的垂直平分线 交 BC 于点 E ,∠ B = 70° ,∠ FAE = 19° ,则∠ C = ____ 度. 点 D 在线段 AB 的垂直平分线上. 11 .如图,在△ ABC 中,∠ C = 90° ,∠ A = 30° , BD 平分∠ ABC 交 AC 于点 D ,则点 D 在 ________________________ . 24 线段 AB 的垂直平分线上 12 .如图,在△ ABC 中, AB = AC , O 是△ ABC 内一点, 且 OB = OC ,点 P 是直线 OA 上一动点,求证: PB = PC. 证明:∵ AB = AC , OB = OC , ∴点 A , O 均在线段 BC 的垂直平分线上. ∵两点确定一条直线,∴直线 OA 垂直平分线段 BC ,∴ PB = PC 13 . ( 练习题 3 变式 ) 如图,在 △ ABC 中, AD 垂直平分 BC , 点 E 在 BC 的延长线上,且满足 AB + BD = DE , 求证:点 C 在线段 AE 的垂直平分线上. 证明: ∵ AD 是 BC 的垂直平分线, ∴ AB = AC , BD = CD. ∵ AB + BD = DE , ∴ AC + CD = DE , ∴ AC = DE - CD = CE , ∴ 点 C 在线段 AE 的垂直平分线上 14 .如图,在 △ ABC 中, ∠ A = 60° ,点 D 是 BC 边的中点, DE ⊥ BC , ∠ ABC 的平分线 BF 交 DE 于 △ ABC 内一点 P ,连结 PC. (1) 若 ∠ ACP = 24° ,求 ∠ ABP 的度数; (2) 若 ∠ ACP = m° , ∠ ABP = n° , 请直接写出 m , n 满足的关系式: ______________ . m + 3n = 120 解: (1) ∵ 点 D 是 BC 边的中点, DE ⊥ BC , ∴ PB = PC , ∴∠ PBC = ∠ PCB. ∵ BP 平分 ∠ ABC , ∴∠ PBC = ∠ ABP , ∴∠ PBC = ∠ PCB = ∠ ABP. ∵∠ A = 60° , ∠ ACP = 24° , ∴∠ PBC + ∠ PCB + ∠ ABP = 180° - 60° - 24° , ∴ 3 ∠ ABP = 96° , ∴∠ ABP = 32° (2)m + 3n = 120 提示: ∵ 点 D 是 BC 边的中点, DE ⊥ BC , ∴ PB = PC , ∴∠ PBC = ∠ PCB. ∵ BP 平分 ∠ ABC , ∴∠ PBC = ∠ ABP , ∴∠ PBC = ∠ PCB = ∠ ABP = n°. ∵∠ A = 60° , ∠ ACP = m° , ∴∠ PBC + ∠ PCB + ∠ ABP = 180° - 60° - m° , ∴ 3 ∠ ABP = 120° - m° , ∴ 3n° + m° = 120° ,故答案为 m + 3n = 120 15 .如图, △ ABC 中, AB = AC , ∠ BAC = 54° , ∠ BAC 的平分线与 AB 的垂直平分线 OD 交于点 O ,将 ∠ C 沿 EF(E 在 BC 上, F 在 AC 上 ) 折叠,点 C 与点 O 恰好重合,则 ∠ OEC 为 _______ 度. . 108 ∵ DO 是 AB 的垂直平分线, ∴ OA = OB , ∴∠ ABO = ∠ BAO = 27° , ∴∠ OBC = ∠ ABC - ∠ ABO = 63° - 27° = 36°. ∵ AO 为 ∠ BAC 的平分线, AB = AC , ∴△ AOB ≌△ AOC( S . A . S .) , ∴ OB = OC , ∴ 点 O 在 BC 的垂直平分线上, ∴∠ OCB = ∠ OBC = 36°. ∵ 将 ∠ C 沿 EF(E 在 BC 上, F 在 AC 上 ) 折叠, 点 C 与点 O 恰好重合, ∴ OE = CE , ∴∠ COE = ∠ OCB = 36° , ∴∠ OEC = 180° - ∠ COE - ∠ OCB = 180° - 36° - 36° = 108° 16 .如图,在 △ ABC 中, ∠ B = 22.5° ,边 AB 的垂直平分线 l 交 BC 于点 D , DF ⊥ AC 于点 F ,并与 BC 边上的高 AE 交于点 G. 求证: EG = EC. 证明:连结 AD , ∵ l 垂直平分 AB , ∴ AD = BD , ∴∠ BAD = ∠ B = 22.5° , ∴∠ ADE = ∠ BAD + ∠ B = 45°. ∵ AE ⊥ BC , ∴∠ DAE = 90° - 45° = 45° , ∴∠ ADE = ∠ DAE , ∴ AE = DE. ∵ DF ⊥ AC , AE ⊥ BC , ∴∠ EDG + ∠ C = 90° , ∠ EAC + ∠ C = 90° , ∴∠ EDG = ∠ EAC. 又 ∵∠ DEG = ∠ AEC = 90° , ∴△ DEG ≌△ AEC( A . S . A .) , ∴ EG = EC查看更多