- 2021-05-11 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级下册数学讲义-小升初复习: 第06讲 方程法解图形问题(下)(解析版)全国通用
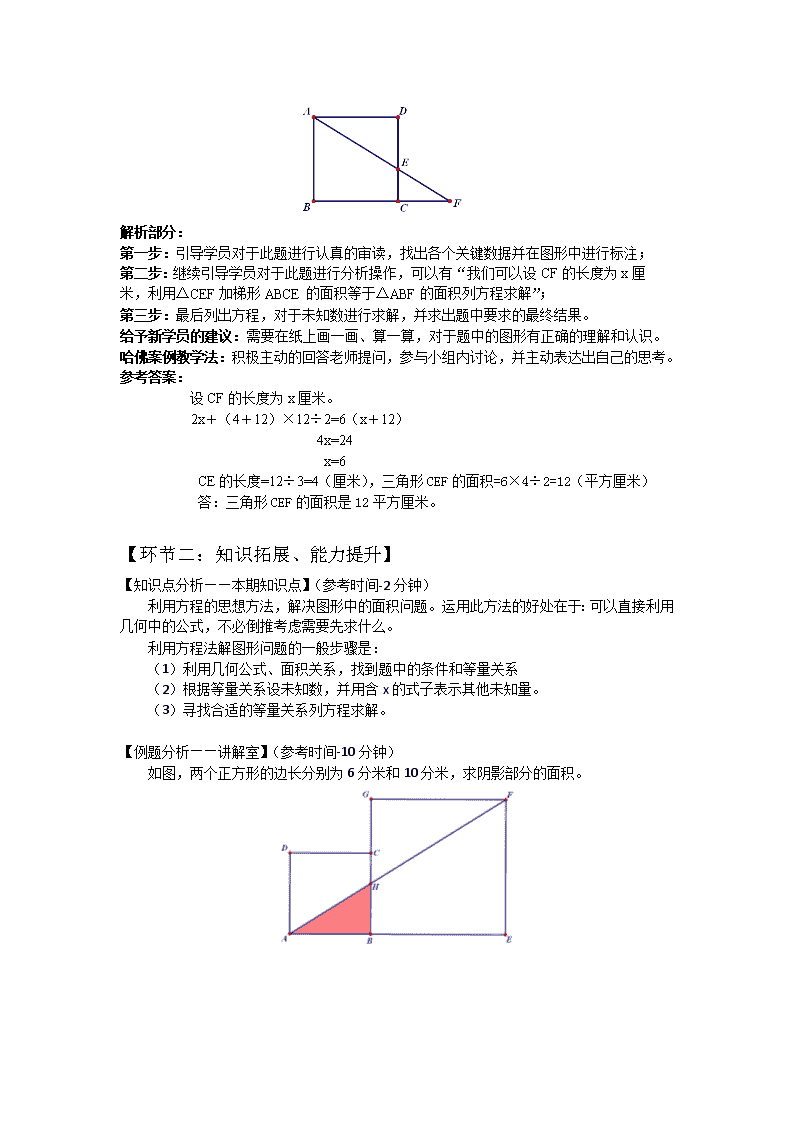
第06讲 方程法解图形问题(下) 教学目标: 1、列出非所求未知数,间接解答图形问题; 2、将方程代数途径与几何问题紧密的结合起来; 3、进一步培养学员的符号感、图形感和巧妙解题的意识。 教学重点: 图形中隐藏等量关系的寻找和利用以及公式的选择。 教学难点: 等积变形在列方程或用含x的式子表示未知量中的应用。 教学过程: 【环节一:预习讨论,案例分析】 【知识回顾——温故知新】(参考时间-2分钟) 利用方程的思想方法,解决图形中的面积问题。运用此方法的好处在于:可以直接利用几何中的公式,不必倒推考虑需要先求什么。 利用方程法解图形问题的一般步骤是: (1)利用几何公式、面积关系,找到题中的条件和等量关系 (2)根据等量关系设未知数,并用含x的式子表示其他未知量。 (3)寻找合适的等量关系列方程求解。 【知识回顾——上期巩固】(参考时间-3分钟) 大小两个正方形,已知它们的边长之差为12厘米,面积之差为984平方厘米,那么小正方形的边长为多少厘米? 解析部分: 第一步:引导学员对于此题进行认真的审读,找出各个关键数据进行相应的标注; 第二步:继续引导学员对于此题进行相应的计算操作,可以有“最终求的是两正方形的面积之和,我们可以先求出两个正方形的面积再求和。本题的等量关系是边长差等于12厘米,面积差等于984平方厘米。我们可以设小正方形的边长为x厘米,那么大正方形的边长就可以表示为(x+12)厘米”; 第三步:最后列出方程,并对于方程进行求解,进行结果的正确性和合理性的验证计算。 给予新学员的建议:分析各数据的意义,然后找出其之间的关联,纸上画一画、写一写。 哈佛案例教学法:引导学员进行问题的小组内讨论,鼓励学员积极说出自己的想法和思考。 参考答案: 设小正方形的边长为x厘米,大正方形的边长为x+12厘米。 12(x+12)+12x=984 24x=840 x=35 答:小正方形的边长为35厘米。 【预习题分析——本期预习】(参考时间-7分钟) 如图,正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,求三角形CEF的面积。 解析部分: 第一步:引导学员对于此题进行认真的审读,找出各个关键数据并在图形中进行标注; 第二步:继续引导学员对于此题进行分析操作,可以有“我们可以设CF的长度为x厘米,利用△CEF加梯形ABCE的面积等于△ABF的面积列方程求解”; 第三步:最后列出方程,对于未知数进行求解,并求出题中要求的最终结果。 给予新学员的建议:需要在纸上画一画、算一算,对于题中的图形有正确的理解和认识。 哈佛案例教学法:积极主动的回答老师提问,参与小组内讨论,并主动表达出自己的思考。 参考答案: 设CF的长度为x厘米。 2x+(4+12)×12÷2=6(x+12) 4x=24 x=6 CE的长度=12÷3=4(厘米),三角形CEF的面积=6×4÷2=12(平方厘米) 答:三角形CEF的面积是12平方厘米。 【环节二:知识拓展、能力提升】 【知识点分析——本期知识点】(参考时间-2分钟) 利用方程的思想方法,解决图形中的面积问题。运用此方法的好处在于:可以直接利用几何中的公式,不必倒推考虑需要先求什么。 利用方程法解图形问题的一般步骤是: (1)利用几何公式、面积关系,找到题中的条件和等量关系 (2)根据等量关系设未知数,并用含x的式子表示其他未知量。 (3)寻找合适的等量关系列方程求解。 【例题分析——讲解室】(参考时间-10分钟) 如图,两个正方形的边长分别为6分米和10分米,求阴影部分的面积。 Ø 本题中有哪些等量关系? Ø 设哪条线段或者哪个面积作为未知数? 解析部分: 第一步:引导学员对于此题进行认真仔细的审读,并对关键数据进行相应的标注; 第二步:继续引导学员对于此题进行具体的操作计算,我们可以利用S△ABH+S梯形BHFE=S△AEF,设BH=x分米,利用含x的式子表示图形的面积; 第三步:最后列出方程,对于方程进行求解,进行结果的正确性和合理性的验证和分析。 给予新学员的建议:认真仔细的观察图形,对于各个数据所指代的具体意义有正确的认识。 哈佛案例教学法:调动学员产生对于此题的热情,组织活跃的小组讨论,鼓励纸上实际操作。 参考答案: 设BH的长度为x分米。 3x+5(x+10)=80 8x=30 x=3.75 3.75×6÷2=11.25(平方厘米) 答:阴影部分面积11.25平方厘米。 【环节三:阶段复习】 【游戏环节——游乐场】(参考时间-2分钟) 游戏名称:五子棋 游戏规则: 两人一组,进行比赛,先将横向、竖向、斜向形成连续的相同色五个棋子的一方为胜。 参考答案:略。 【练习分析——练习场(一)】(参考时间-7分钟) 一个正方形,如果把它的一组对边各减少25厘米,另一组对边各减少10厘米;或者把它的一组对边各减少22.5厘米,另一组对边各各减少15厘米,则剩下的图形面积相等。原正方形面积是多少平方厘米? Ø 本题中有哪些等量关系? Ø 变化之后的图形是什么基本图形? 解析部分: 第一步:引导学员对于此题进行认真的审读,找出各个关键数据并在图形中进行标注; 第二步:继续引导学员对于此题进行分析操作,可以有“变化后的图形是长方形,本题中的等量关系是两次减少的图形面积相等。我们可以设原正方形的边长为x厘米,那么减少的部分我们就可以利用含x的式子表示出来”; 第三步:最后列出方程,对于未知数进行求解,并求出题中要求的最终结果。 给予新学员的建议:根据题意,分析各数据之间的关联,并可以进行准确而迅速的基础运算。 哈佛案例教学法:引导学员对于此题的积极思考,并鼓励学员能把自己的观点主动表达出来。 参考答案: 设原正方形的边长为x厘米。 25x+10(x-25)=22.5x+15(x-22.5) 2.5x=87.5 x=35 35×35=1225(平方厘米) 答:原正方形的面积是1225平方厘米。 【练习分析——练习场(二)】(参考时间-7分钟) 如图,在△ABC中,点E是BC边上的中点,点F是线段AE上的点,其中AE=3AF,已知延长BF与AC相交于D。若三角形ABC的面积为48,请问三角形AED的面积是多少? Ø 作为一题需要利用方程求解的问题,本题等量关系在哪里? Ø 设哪个未知量作为未知数? 解析部分: 第一步:引导学员对于此题进行认真仔细的审读,并对关键数据进行相应的标注; 第二步:继续引导学员对于此题进行具体的操作计算,可以有“ 因为E是中点,所以本题中等量关系可以有ABE的面积等于ACE的面积。我们设AFD的面积x,利用等积变形把其他图形面积用含x表示出来,△DEF=2x,而△CDE的面积无法直接利用含x的式子表示出来,但是我们可以利用△BDE的面积去表示”; 第三步:最后列出方程,对于方程进行求解,进行结果的正确性和合理性的验证和分析。 给予新学员的建议:认真观察题目中的图形,纸上实际操作尝试找出问题的解决突破口。 哈佛案例教学法:鼓励学员积极地参与小组内的讨论,并积极参与到课堂的各个环节中。 参考答案: 设△ADF的面积是x。 x+2x+(48÷2÷3×2+2x)=48÷2 5x=8 x=1.6 又由于AE=3AF,则 △AED的面积=1.6×3=4.8 答:△AED的面积是4.8。 【本节总结】 利用方程的思想方法,解决图形中的面积问题。运用此方法的好处在于:可以直接利用几何中的公式,不必倒推考虑需要先求什么。 利用方程法解图形问题的一般步骤是: (1)利用几何公式、面积关系,找到题中的条件和等量关系 (2)根据等量关系设未知数,并用含x的式子表示其他未知量。 (3)寻找合适的等量关系列方程求解。查看更多