- 2021-05-06 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级下册数学讲义-小升初复习:第06讲 重叠问题 (下) (解析版)全国通用
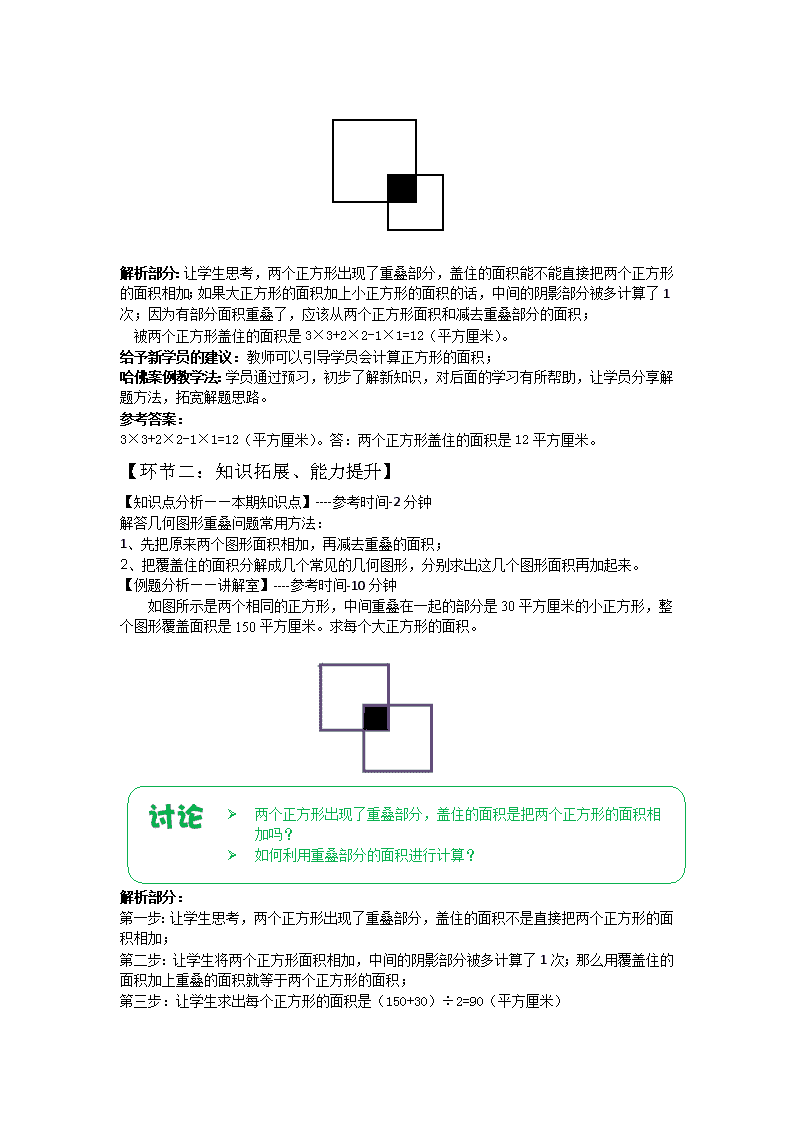
第06讲 重叠问题(下) 教学目标: 1、掌握解决几何图形重叠问题的一些基本策略,体验解决问题策略的多样性; 2、鼓励学员尽可能多的在纸上画一画,写一写重叠问题的相关问题,提升计算准度和速度; 3、进一步丰富对直观的认识,发展形象思维,养成善于观察、善于思考的良好学习品质。教学重点: 掌握几何图形重叠问题的解题思路和方法,体验解决问题策略的多样性。 教学难点: 掌握解决重叠问题的一些基本策略。 教学过程: 【环节一:预习讨论,案例分析】 【知识回顾——温故知新】----参考时间-2分钟 解答重叠问题常用方法: 解答重叠问题,必须从条件入手,要认真地进行分析,有时还要画出图示,借助图进行思考,找到哪些是重复的,重复了几次,明确求出的是哪一部分,从而找到解答方法。 【知识回顾——上期巩固】----参考时间-3分钟 有四块各长厘米的木板,钉成一块木板(如图),中间钉在一起重叠的部分是厘米,钉成的木板长多少厘米? 解析部分:引导学生思考, 画图分析 四根木板的长度是80×4=320(厘米)。钉在一起后,共有3个10厘米的重叠,要从总长度中把这多算的30厘米减掉,才是现在木板的长度. 给予新学员的建议:教师可以引导学员画图分析题意 哈佛案例教学法:鼓励学生独立完成,课堂上分享解题方法。 参考答案: 80×4-10×3=290(厘米) 答:钉成的木板长290厘米。 【预习题分析——本期预习】----参考时间-7分钟 如图所示,桌上有两个部分重叠的正方形,大正方形的边长为3厘米,小正方形的边长为2厘米,重叠部分是一个边长为1厘米的正方形,两个正方形盖住多大面积? 解析部分:让学生思考,两个正方形出现了重叠部分,盖住的面积能不能直接把两个正方形的面积相加;如果大正方形的面积加上小正方形的面积的话,中间的阴影部分被多计算了1次;因为有部分面积重叠了,应该从两个正方形面积和减去重叠部分的面积; 被两个正方形盖住的面积是3×3+2×2-1×1=12(平方厘米)。 给予新学员的建议:教师可以引导学员会计算正方形的面积; 哈佛案例教学法:学员通过预习,初步了解新知识,对后面的学习有所帮助,让学员分享解题方法,拓宽解题思路。 参考答案: 3×3+2×2-1×1=12(平方厘米)。答:两个正方形盖住的面积是12平方厘米。 【环节二:知识拓展、能力提升】 【知识点分析——本期知识点】----参考时间-2分钟 解答几何图形重叠问题常用方法: 1、先把原来两个图形面积相加,再减去重叠的面积; 2、把覆盖住的面积分解成几个常见的几何图形,分别求出这几个图形面积再加起来。 【例题分析——讲解室】----参考时间-10分钟 如图所示是两个相同的正方形,中间重叠在一起的部分是30平方厘米的小正方形,整个图形覆盖面积是150平方厘米。求每个大正方形的面积。 Ø 两个正方形出现了重叠部分,盖住的面积是把两个正方形的面积相加吗? Ø 如何利用重叠部分的面积进行计算? 解析部分: 第一步:让学生思考,两个正方形出现了重叠部分,盖住的面积不是直接把两个正方形的面积相加; 第二步:让学生将两个正方形面积相加,中间的阴影部分被多计算了1次;那么用覆盖住的面积加上重叠的面积就等于两个正方形的面积; 第三步:让学生求出每个正方形的面积是(150+30)÷2=90(平方厘米) 给予新学员的建议:引导学员理解几何图形的重叠部分如何计算; 哈佛案例教学法:引导学生进行分组讨论,让学生根据讨论问题找到解题方法。 参考答案: (150+30)÷2=90(平方厘米) 答:每个正方形的面积是90平方厘米。 【环节三:阶段复习】 【游戏环节——游乐场】----参考时间-2分钟 游戏名称:以物换物 游戏规则: 老师准备些各种各样的小物品,设置一些交换关系。让后分发给学生一些物品,老师保 留一些。让学生模仿以物换物的市场买卖,可以和学生换,也可以和老师换,最后看看 谁赚了,谁亏了。 参考答案:略 【练习分析——练习场(一)】----参考时间-7分钟 兔看到桌面有两张纸,有一部分重叠在一起,长方形的纸的长15厘米,宽8厘米,三角形纸的面积是50平方厘米,阴影部分是三角形与长方形纸的重叠部分,已知阴影部分面 积是20平方厘米,三角形与长方形覆盖住的面积是多少平方厘米? Ø 被覆盖住的面积是大三角形的面积加大正方形的面积吗? Ø 如何利用重叠原理解决此类面积问题? 解析部分:引导学员思考: 方法一:大长方形+两个小三角形; 方法二:大三角形面积+“L”形的面积; 方法三:将大长方形和大三角形的面积相加,因为有部分面积重叠了,应该再减去阴影部分的面积。 给予新学员的建议:让学员根据题意算出中间重叠部分。 哈佛案例教学法:引导学生进行分组讨论,让学生根据讨论问题找到解题方法。 参考答案: 方法一: 两个小三角形的面积:50-20=30(平方厘米) 大长方形面积:15×8=120(平方厘米) 纸片覆盖的面积是:120+30=150(平方厘米) 方法二: 一个“L”形状面积:15×8-20=100(平方厘米) 大三角形:50平方厘米 纸片覆盖的面积是:100+50=150(平方厘米) 方法三: 大长方形面积:15×8=120(平方厘米) 大三角形面积:50平方厘米 纸片覆盖的面积是:120+50-20=150(平方厘米) 答:三角形与长方形覆盖住的面积是150平方厘米。 【练习分析——练习场(二)】----参考时间-7分钟 如图所示,一个长方形与一个三角形(有一个角是直角,夹直角的两条边相等)重叠在一起,长方形的长为20厘米,宽为10厘米,大三角形的面积为200平方厘米,重叠部分的面积为160平方厘米,求三角形与长方形覆盖住的面积是多少平方厘米? Ø 被覆盖住的面积是由哪些图形组成的? Ø 如何利用重叠原理解决此类面积问题? 解析部分:让学生先求出长方形面积是20×10=200(平方厘米),长方形面积加上三角形的面积是200+200=400(平方厘米),重叠部分的面积是160平方厘米,所以,覆盖住的面积是400-160=240(平方厘米)。 给予新学员的建议:引导学员计算长方形的面积; 哈佛案例教学法:引导学生进行分组讨论,让学生根据讨论问题找到解题方法。 参考答案: 长方形面积是20×10=200(平方厘米) 覆盖住的面积是200+200-160=240(平方厘米)。 【本节总结】 解答几何图形重叠问题常用方法: 1、先把原来两个图形面积相加,再减去重叠的面积; 2、把覆盖住的面积分解成几个常见的几何图形,分别求出这几个图形面积再加起来。查看更多