- 2021-05-11 发布 |
- 37.5 KB |
- 28页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【新教材】2020-2021学年高中人教A版数学必修第二册课件:6-1 平面向量的概念
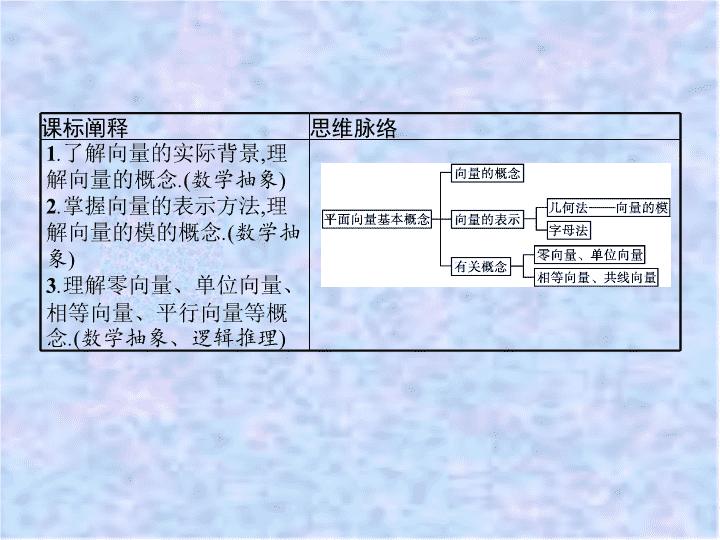
6.1 平面向量的概念 课标阐释 思维脉络 1 . 了解向量的实际背景 , 理解向量的概念 . ( 数学抽象 ) 2 . 掌握向量的表示方法 , 理解向量的模的概念 . ( 数学抽象 ) 3 . 理解零向量、单位向量、相等向量、平行向量等概念 . ( 数学抽象、逻辑推理 ) 激趣诱思 知识点拨 你昨天听天气预报了吗 ? 今天白天的天气情况如何 ? 温度 15 ~ 32 ℃ , 东南风 3 ~ 4 级 . 天气情况中涉及两个量 : 一个是温度 , 另一个是风力 . 前者在选定单位后 , 用一个实数就可以确切地表示 ; 而后者则不同 , 除说明它的大小外 , 同时还必须说明它的方向 . 回顾学习数的概念我们可以从一支笔、一棵树、一本书 …… 中抽象出只有大小的数量 “1” . 类似地 , 我们可以对力、位移 …… 这些量进行抽象 , 形成一种新的量 , 即本节知识 —— 向量 . 激趣诱思 知识点拨 知识点一、向量的概念 1 . 向量 : 在数学中 , 我们把既有 大小 又有 方向 的量叫做向量 . 2 . 数量 : 把只有 大小 没有 方向 的量称为数量 . 名师点析 向量不能比较大小 , 这是因为向量是由大小和方向两方面确定的 . 向量的大小是代数特征 , 方向是几何特征 . 微思考 在物理上 , 位移和距离这两个量有什么不同 ? 提示 : 位移既有大小又有方向 , 距离只有大小没有方向 . 激趣诱思 知识点拨 知识点二、向量的几何表示及相关概念 2 . 有向线段的三个要素 : 起点 、 方向 、 长度 . 知道了有向线段的起点、方向和长度 , 它的终点就唯一确定了 . 4 . 长度为 0 的向量叫做零向量 , 记作 0 . 5 . 长度等于 1 个单位长度的向量 , 叫做单位向量 . 6 . 向量也可以用字母 a , b , c , … 表示 . 激趣诱思 知识点拨 名师点析 (1) 零向量的长度为 0, 方向不确定 . (2) 单位向量只规定了向量的大小 ( 模长为 1), 并没有规定向量的方向 , 所以同一起点的单位向量有无数个 , 它们的终点构成一个单位圆 . 激趣诱思 知识点拨 微练习 (1) 下列说法正确的是 ( ) A. 身高是一个向量 B. 温度有零上温度和零下温度之分 , 故温度是向量 C. 有向线段由方向和长度两个要素确定 ( 2) 下列说法正确的是 ( ) A. 向量的模是一个正实数 B. 零向量没有方向 C. 单位向量的模等于 1 个单位长度 D. 零向量就是实数 0 激趣诱思 知识点拨 解析 : (1) 有向线段 的 起点与终点互换 , 其方向相反 , 长度相等 , 故 D 项正确 . (2) 向量的模是一个非负实数 ; 零向量的方向是任意的 , 但它不是实数 0, 故 A,B,D 均错 , 只有 C 项正确 . 答案 : (1)D (2)C 激趣诱思 知识点拨 知识点三、相等向量与共线向量 1 . 方向 相同或相反 的 非零 向量叫做平行向量 . 向量 a , b 平行 , 记作 a ∥ b . 平行向量也叫做共线向量 . 2 . 我们规定 : 零向量与任意向量平行 , 即对于任意向量 a , 都有 0 ∥ a . 3 . 长度 相等且 方向 相同的向量叫做相等向量 . 两个向量 a 与 b 相等 , 记作 a = b . 名师点析 向量共线包括四种情况 : 方向相同 , 模相等 ; 方向相同 , 模不等 ; 方向相反 , 模相等 ; 方向相反 , 模不等 . 激趣诱思 知识点拨 微练习 下列说法正确的是 ( ) A. 所有单位向量都是相等向量 B. 与实数类似 , 对于两个向量 a , b , 有 a = b , a > b , a < b 三种关系 C. 两个向量平行时 , 表示向量的有向线段所在的直线一定平行 D. 若两个向量是共线向量 , 则向量所在的直线可以平行 , 也可以重合 解析 : 所有单位向量的模都相等 , 都为 1, 但方向不确定 , 故 A 不正确 . 向量不能比较大小 , 故 B 不正确 ; 由平行向量的定义知 ,D 正确 ,C 不正确 . 答案 : D 探究一 探究二 探究三 素养形成 当堂检测 平面向量的相关概念 例 1 已知下列说法 : ① 若 | a |= 0, 则 a 为零向量 ; ② 若 | a |=| b | , 则 a = b ; ③ 若 a ∥ b , 则 | a |=| b | ; ④ 两个有共同起点 , 而且相等的向量 , 其终点必相同 . 其中正确的有 ( ) A.1 个 B . 2 个 C . 3 个 D . 4 个 解析 : ① 正确 ; ② 由 | a |=| b | 得 a 与 b 的模相等 , 但不确定方向 , 故 ② 错误 ; ③ 错误 ; ④ 正确 . 答案 : B 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 明确向量及其相关概念的联系与区别 (1) 区分向量与数量 . 向量既强调大小 , 又强调方向 , 而数量只与大小有关 . (2) 明确向量与有向线段的区别 . 有向线段有三要素 , 起点、方向、长度 . 只要起点不同 , 另外两个要素相同也不是同一条有向线段 , 但决定向量的要素只有两个 , 大小和方向 , 与表示向量的有向线段的起点无关 . (3) 零向量和单位向量都是通过模的大小来确定的 , 零向量的方向是任意的 . (4) 平行向量也叫共线向量 , 当两共线向量的方向相同且模相等时 , 两向量为相等向量 . (5) 向量之间不能比较大小 , 但它们的模可以比较大小 . 探究一 探究二 探究三 素养形成 当堂检测 变式训练 1 给出以下说法 : ① 直角坐标平面上的 x 轴、 y 轴都是向量 ; ② 零向量的长度为零 , 方向是任意的 ; ③ 若 a , b 都是单位向量 , 则 a = b ; ④ 有向线段就是向量 ; ⑤ 单位向量大于零向量 . 其中正确说法的序号是 . 解析 : 直角坐标平面上的 x 轴、 y 轴是数轴 , 但不是向量 , 故 ① 错误 ; 由零向量的定义可知 ② 正确 ; 若 a , b 都是单位向量 , 则它们的模相等 , 但不一定方向相同 , 故 ③ 错误 ; 有向线段可以用来表示向量 , 但它不是向量 , 故 ④ 错误 ; 单位向量的模大于零向量的模 , 但不能说单位向量大于零向量 , 向量之间不能比较大小 , 故 ⑤ 错误 . 答案 : ② 探究一 探究二 探究三 素养形成 当堂检测 平面向量的表示 例 2 在如图所示的坐标纸上 ( 每个小方格的边长均为 1), 用直尺和圆规画出下列向量 : 分析 先确定起点 , 再根据大小和方向确定出终点 , 即可画出向量 . 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 向量的表示方法 (1) 几何法 : 准确画出向量的方法是先确定向量的起点 , 再确定向量的方向 , 最后根据向量的大小确定向量的终点 . (2) 字母法表示向量的注意事项 : 在书写字母表示向量时不要忘记字母上的箭头 . 探究一 探究二 探究三 素养形成 当堂检测 变式训练 2 如图 , B , C 是线段 AD 的三等分点 , 分别以图中各点为起点和终点 , 可以写出 个向量 . 解析 : 由向量的几何表示可知 , 可以写出 12 个向量 , 它们分别 是 答案 : 12 探究一 探究二 探究三 素养形成 当堂检测 寻找相等向量和共线向量 例 3 如图所示 , 四边形 ABCD 为边长为 3 的正方形 , 把各边三等分后 , 共有 16 个交点 , 从中选取两个交点作为向量的起点和终点 , 则 与 平行 且长度为 2 的 向量有哪些 ?( 在图中标出相关字母 , 写出这些向量 ) 分析 所求向量有以下两个特征 :(1) 表示此向量的有向线段所在直线与 AC 平行或重合 . (2) 长度等于边长为 2 的正方形的对角线的长度 . 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 相等向量与共线向量的探求方法 (1) 寻找相等向量 : 先找与已知向量长度相等的向量 , 再确定哪些与已知向量同向 . (2) 寻找共线向量 : 先找与表示已知向量的有向线段平行或共线的线段 , 再构造同向与反向的向量 , 注意不要漏掉以表示已知向量的有向线段的终点为起点 , 起点为终点的向量 . 探究一 探究二 探究三 素养形成 当堂检测 数形结合思想在向量中的应用 典例 已知 A 1 , A 2 , … , A 8 是圆 O 的八个等分点 , 则在以 A 1 , A 2 , … , A 8 以及圆心这九个点中的任意两点为起点与终点的向量中 , 模等于半径长的向量有多少个 ? 模等于半径长 的 倍 的向量有多少个 ? 探究一 探究二 探究三 素养形成 当堂检测 (2) 以 A 1 , A 2 , … , A 8 的一部分点为顶点的圆 O 的内接正方形有两个 , 一个是正方形 A 1 A 3 A 5 A 7 , 另一个是正方形 A 2 A 4 A 6 A 8 . 在所有的向量中 , 只有这两个正方形的边 ( 看成有向线段 , 每一边对应两个向量 ) 的长度为半径长 的 倍 , 所以模为半径长 的 倍 的向量共有 4 × 2 × 2 = 16( 个 ) . 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 1 . 下列各量中是向量的是 ( ) A. 时间 B. 速度 C. 面积 D. 长度 解析 : 速度既有大小又有方向 , 是向量 , 其余均是数量 . 答案 : B 2 . 给出以下说法 : ① 零向量的长度为零 , 方向是任意的 ; ② 共线向量是在同一条直线上的向量 ; ③ 向量 相等 ; ④ 若两个向量是相等向量 , 则它们一定是共线向量 . 其中正确说法的序号是 ( ) A. ①④ B. ② C. ①③④ D. ②③ 解析 : 根据零向量的定义可知 ① 正确 ; 共线向量可以是在同一条直线上的向量 , 也可以是所在直线互相平行的向量 , 故 ② 错误 ; 向量 模 相等 , 方向相反 , 故 ③ 错误 . ④ 显然正确 , 故选 A . 答案 : A 探究一 探究二 探究三 素养形成 当堂检测 答案 : D 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 5 . 如图 , 在正方形 ABCD 中 , M , N 分别为 AB 和 CD 的中点 , 在以 A , B , C , D , M , N 为起点与终点的所有有向线段表示的向量中 , 相等的非零向量共有多少对 ? 探究一 探究二 探究三 素养形成 当堂检测查看更多