- 2021-05-10 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学上册第十三章轴对称章末复习课件新版 人教版
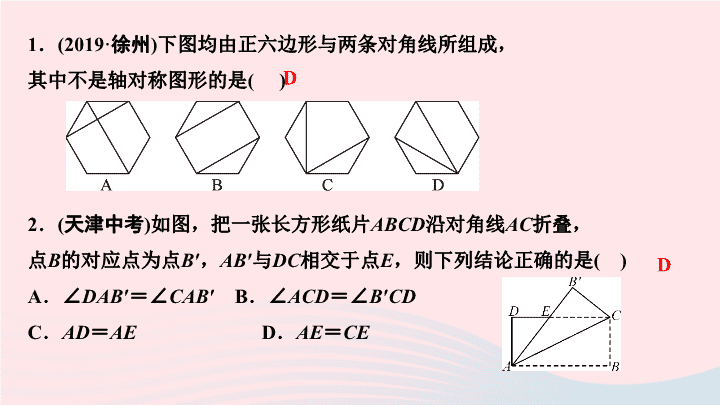
第十三章 轴对称 章末复习 (三) 轴对称 1 . (2019 · 徐州 ) 下图均由正六边形与两条对角线所组成, 其中不是轴对称图形的是 ( ) 2 . ( 天津中考 ) 如图,把一张长方形纸片 ABCD 沿对角线 AC 折叠, 点 B 的对应点为点 B ′ , AB ′ 与 DC 相交于点 E ,则下列结论正确的是 ( ) A .∠ DAB ′ =∠ CAB ′ B .∠ ACD =∠ B ′ CD C . AD = AE D . AE = CE D D 3 . ( 甘孜州中考 ) 在平面直角坐标系中,点 A (2 , 3) 与点 B 关于 y 轴对称, 则点 B 的坐标为 ( ) A . ( - 2 , 3) B . ( - 2 ,- 3) C . (2 ,- 3) D . ( - 3 ,- 2) 4 .在 4×4 的网格中有五个同样大小的正方形阴影如图所示摆放, 移动其中一个阴影正方形到空白方格中, 与其余四个阴影正方形组成的新图形是一个轴对称图形, 这样的移法共有 ____ 种. A 13 5 .如图,在平面直角坐标系中,△ ABC 三个顶点的坐标分别 为 A ( - 2 , 1) , B ( - 3 , 5) , C ( - 5 , 2) ,画出△ ABC 关于 x 轴对称的△ A 1 B 1 C 1 . 6 . ( 洛阳东方二中模拟 ) 如图, AB = AC , ∠ A = 40° , AB 的垂直平分线 DE 交 AC 于点 E ,垂足为点 D ,则 ∠ EBC 的度数是 ( ) A . 30° B . 40° C . 70° D . 80° A 7 .为了推进农村新型合作医疗制度改革, 准备在某镇新建一个医疗点 P ,使 P 到该镇所属 A 村, B 村, C 村的村委会 所在地的距离都相等 ( A , B , C 不在同一直线上,地理位置如图所示 ) , 请你用尺规作图的方法确定点 P 的位置. 要求:写出已知、求作,不写作法,保留作图痕迹. 8 . ( 郑州期中 ) 如图,在 △ ABC 中, AB 边的垂直平分线 l 1 ,交 BC 于点 D , AC 边的垂直平分线 l 2 交 BC 于点 E , l 1 与 l 2 相交于点 O , △ ADE 的周长为 6 cm. (1) 求 BC 的长; (2) 分别连接 OA , OB , OC ,若 △ OBC 的周长为 16 cm ,求 OA 的长. 解: (1)6 cm (2)5 cm 9 .如图,在△ ABC 中, AB = AC , AD 平分∠ BAC , DE ⊥ AB , DF ⊥ AC , E , F 分别为垂足,则下列四个结论: ①∠ DEF = ∠ DFE ; ② AE = AF ; ③ AD 平分 ∠ EDF ; ④ AD 垂直平分 EF . 其中正确的有 ( ) A . 1 个 B . 2 个 C . 3 个 D . 4 个 D 10 .如图,在△ ABC 中, AB = BC , AB = 12 cm , F 是 AB 边上一点, 过点 F 作 FE ∥ BC 交 AC 于点 E ,过点 E 作 ED ∥ AB 交 BC 于点 D , 则四边形 BDEF 的周长是 _____cm. 24 11 . (2019· 重庆 ) 如图,在 △ ABC 中, AB = AC , AD ⊥ BC 于点 D . (1) 若 ∠ C = 42° ,求 ∠ BAD 的度数; (2) 若点 E 在边 AB 上, EF ∥ AC 交 AD 的延长线于点 F . 求证: AE = FE . 解: (1) ∵ AB = AC , AD ⊥ BC 于点 D , ∴∠ BAD = ∠ CAD , ∠ ADC = 90° , 又 ∠ C = 42° , ∴∠ BAD = ∠ CAD = 90° - 42° = 48° (2) ∵ AB = AC , AD ⊥ BC 于点 D , ∴∠ BAD = ∠ CAD , ∵ EF ∥ AC , ∴∠ F = ∠ CAD , ∴∠ BAD = ∠ F , ∴ AE = FE 12 . ( 南阳期中 ) 如图, △ ABC 中, AD 平分 ∠ BAC , AD ⊥ CD , 垂足为 D , DE ∥ AB 交 AC 于点 E . 求证: AE = CE . 证明: ∵ AD 是 ∠ BAC 的平分线, ∴∠ BAD = ∠ DAC . ∵ DE ∥ AB , ∴∠ EDA = ∠ BAD , ∴∠ EAD = ∠ EDA , ∴ AE = DE . ∵ AD ⊥ CD , ∴∠ CAD + ∠ ACD = 90° , ∠ EDA + ∠ EDC = 90°. ∵∠ EDA = ∠ EAD , ∴∠ EDC = ∠ ACD , ∴ DE = CE , ∴ AE = CE 13 .下面给出的几种三角形: ① 有两个角为 60° 的三角形; ② 三个外角都相等的三角形; ③ 一边上的高也是这边上的中线的三角形; ④ 有一个角为 60° 的等腰三角形. 其中是等边三角形的有 ( ) A . 4 个 B . 3 个 C . 2 个 D . 1 个 B 14 .如图, AD 是 △ ABC 的中线, ∠ ADC = 60° , BC = 6 , 把 △ ABC 沿直线 AD 折叠,点 C 落在 C ′ 处,连接 BC ′ ,则 BC ′ 的长为 __ . 3 15 .如图,在等边 △ ABC 中,点 D 为 AC 上一点, CD = CE , ∠ ACE = 60°. (1) 求证: △ BCD ≌△ ACE ; (2) 延长 BD 交 AE 于点 F ,连接 CF ,若 AF = CF , 猜想线段 BF , AF 的数量关系,并证明你的猜想.查看更多