2020_2021学年新教材高中数学第一章集合与常用逻辑用语1
第
1
课时 并集、交集
必备知识
·
自主学习
导思
1.
两个集合的并集是由哪些元素构成的?用什么符号表示两个集合的并集?
2.
两个集合的交集是由哪些元素构成的?用什么符号表示两个集合的交集?
1.
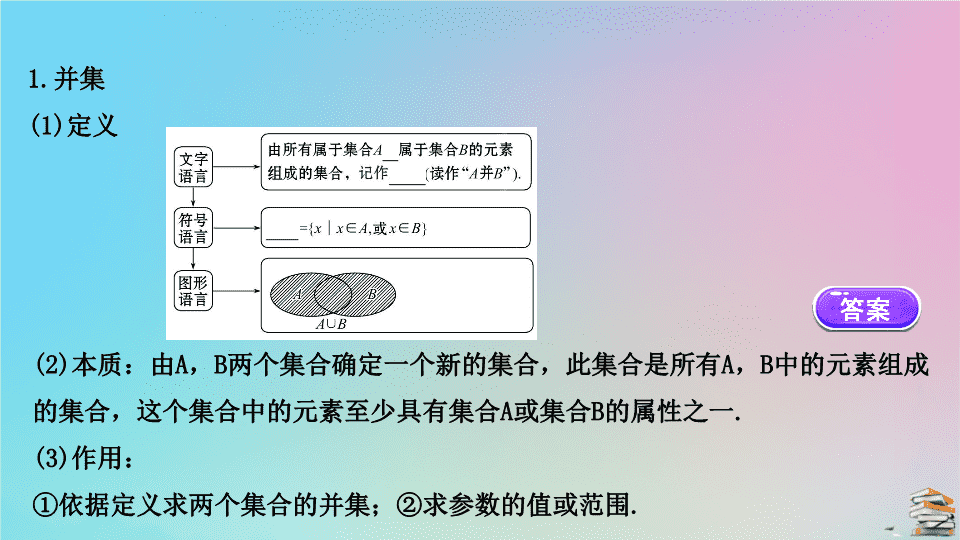
并集
(1)
定义
(2)
本质:由
A
,
B
两个集合确定一个新的集合,此集合是所有
A
,
B
中的元素组成的集合,这个集合中的元素至少具有集合
A
或集合
B
的属性之一
.
(3)
作用:
①依据定义求两个集合的并集;②求参数的值或范围
.
【
思考
】
“
x∈A
或
x∈B
”
包含哪几种情况?如何用
Venn
图表示?
提示:
“
x∈A
或
x∈B
”
这一条件包括下列三种情况:
x∈A
,但
x∉B
;
x∈B
,但
x∉A
;
x∈A
,且
x∈B.
用
Venn
图表示如图所示
.
2.
交集
(1)
定义
(2)
本质:由
A
,
B
两个集合确定一个新的集合,此集合是
A
,
B
中的公共元素组成的集合,这个集合中的元素同时具有集合
A
和集合
B
的属性
.
(3)
作用:①依据定义求两个集合的交集;②求参数的值或范围
.
3.
并集与交集的性质
(1)A∩A=__
,
A∩⌀=
__
.(2)A∪A=__
,
A∪⌀=__.
A
⌀
A
A
【
思考
】
(1)
对于任意两个集合
A
,
B
,
A∩B
与
A
有什么关系?
A∪B
与
A
有什么关系?
(2)
设
A
,
B
是两个集合,若已知
A∩B=A
,
A∪B=B
,则集合
A
与
B
之间有何关系?
提示:
(1)(A∩B)⊆A
,
A⊆(A∪B).(2)
若
A∩B=A
,则
A⊆B
;
若
A∪B=B
,则
A⊆B.
【
基础小测
】
1.
辨析记忆
(
对的打“√”,错的打“
×”)
(1)
若
A
,
B
中分别有
3
个元素,则
A∪B
中必有
6
个元素
. (
)
(2)
若
A∩B=
,则
A=B= . (
)
(3)N∩N
*
=N
*
,
N∪N
*
=N. (
)
(4)
若
x∈(A∩B)
,则
x∈(A∪B). (
)
提示:
(1)
×
.
当
A
,
B
有公共元素时,
A∪B
中元素个数小于
6.
(2)
×
.
例如对于
A={x|x>11}
,
B={x|x<2}
,
A∩B= .
(3)√.
因为
N
*
N
,所以
N∩N
*
=N
*
,
N∪N
*
=N.
(4)√.
因为
(A∩B)⊆(A∪B)
,所以若
x∈(A∩B)
,则
x∈(A∪B).
2.(
教材二次开发:例题改编
)
若集合
A={x|x>-1}
,
B={x|-3
-1} B.{x|x>-3}
C.{x|-1-1}
,
B={x|-3-3}.
3.
已知集合 则
A∩B= (
)
【
解析
】
选
A.
由已知条件可得
A∩B= .
关键能力
·
合作学习
类型一 并集及其应用
(
数学运算
)
角度
1
集合的并集运算
【
典例
】
(2020·
郑州高一检测
)
定义集合的商集运算为
已知集合
A={2
,
4
,
6}
,
B={x|x= -1
,
k∈A}
,
则集合 ∪
B
元素的个数为
(
)
A.7 B.8 C.9 D.10
【
思路导引
】
先求集合
B
是由哪些元素构成的,再依据“商集”的定义求 ,
最后求 ∪
B
并确定其元素个数
.
【
解析
】
选
A.
因为集合的商集运算为
集合
A={2
,
4
,
6}
,
B= ={0
,
1
,
2}
,
所以
所以 所以集合 ∪
B
元素的个数为
7.
角度
2
知并集求参数的值或范围
【
典例
】
(2020·
菏泽高一检测
)
已知集合
A={x|x≤2}
,
B={x|x>a}
,如果
A∪B=R
,那么
a
的取值范围是
_______.
【
思路导引
】
根据题意画数轴,分析实数
a
表示的点所在的位置
.
【
解析
】
根据题意画出数轴,表示集合
A
和
B
,如图所示,
由图可知,实数
a
的取值范围是
{a|a≤2}.
答案:
{a|a≤2}
【
变式探究
】
本例条件若改为“
A={x|x<-1
或
x>5}
,
B={x|a-1}
,
B={x|x<2}
,则
A∩B= (
)
A.{x|x>-1} B.{x|x<2}
C.{x|-10}=
,求实数
p
的取值范围
.
【
思路导引
】
分析题意可知,解答本题可分
A=
和
A≠
两种情况讨论
.
【
解析
】
因为
A∩{x∈R|x>0}=
,
所以若
A=
,则
Δ
=4-4p<0
,得
p>1
;
若
A≠
,则方程
x
2
+2x+p=0
的根都小于或等于
0.
设两根为
x
1
,
x
2
,
则
综上所述,
p≥0.
【
解题策略
】
1.
求集合
A∩B
的方法与步骤
(1)
步骤
①首先要搞清集合
A
,
B
的代表元素是什么
.
②
把所求交集的集合用集合符号表示出来,写成
“
A∩B
”
的形式
.
③
把化简后的集合
A
,
B
的所有公共元素都写出来即可
(
若无公共元素则所求交
集为
).
(2)
方法
①若
A
,
B
的代表元素是方程的根,则应先解方程,求出方程的根后,再求两集合的交集;若集合的代表元素是有序数对,则
A∩B
是指两个方程组成的方程组的解集,解集是点集
.
②
若
A
,
B
是无限数集,可以利用数轴来求解
.
但要注意,利用数轴表示不等式时,含有端点的值用实心点表示,不含有端点的值用空心点表示
.
2.
解答与交集有关的参数问题的依据和关注点
(1)
依据:交集的定义和求交集的方法和过程
.
(2)
关注点:按照条件和集合元素的互异性进行检验
.
【
题组训练
】
1.(2020·
山东新高考模拟
)
设集合
A={(x
,
y)|x+y=2}
,
B={(x
,
y)|y=x
2
}
,
则集合
A∩B= (
)
A.{(1
,
1)} B. {(-2
,
4)}
C. {(1
,
1)
,
(-2
,
4)} D.
【
解析
】
选
C.
首先注意到集合
A
与集合
B
均为点集,联立 解得
从而集合
A∩B={(1
,
1)
,
(-2
,
4)}
,选
C.
2.
若集合
A={x|2x+1>0}
,
B={x|-15}.
(1)
若
A∩B=
,求实数
a
的取值范围
.
(2)
若
A∪B=B
,求实数
a
的取值范围
.
【
解析
】
(1)
因为
A∩B=
,所以
解得
-1≤a≤2.
(2)
因为
A∪B=B
,所以
A⊆B
,所以
a>5
或
a+3<-1
,即
a
的取值范围为
a>5
或
a<-4.
课堂检测
·
素养达标
1.
已知集合
A={x|x
2
-2x=0}
,
B={0
,
1
,
2}
,则
A∩B
等于
(
)
A.{0} B.{0
,
1}
C.{0
,
2} D.{0
,
1
,
2}
【
解析
】
选
C.
因为
A={x|x
2
-2x=0}={0
,
2}
,
B={0
,
1
,
2}
,所以
A∩B={0
,
2}.
2.
已知集合
A={x|x<1}
,
B={x|x<0}
,则
(
)
A.A∩B={x|x<0} B.A∪B=R
C.A∪B={x|x>1} D.A∩B=
∅
【
解析
】
选
A.
因为
A={x|x<1}
,
B={x|x<0}
,
则
A∩B={x|x<0}
,
A∪B={x|x<1}.
3.
若集合
A={x|x≥0}
,且
A∪B=A
,则集合
B
可能是
(
)
A.{1
,
2} B.{x|x≤1}
C.{-1
,
0
,
1} D.R
【
解析
】
选
A.
因为
A∪B=A
,所以
B
⊆
A
,
四个选项中,符合
B⊆A
的只有选项
A.
4.(
教材二次开发:练习改编
)
已知集合
M={x|-35}
,则
M∪N=_____
,
M∩N=_______.
【
解析
】
借助数轴可知:
M∪N={x|x>-5}
,
M∩N={x|-3-5}
{x|-3
查看更多