- 2021-05-10 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版九年级上册数学同步课件-第25章-25列举所有机会均等的结果
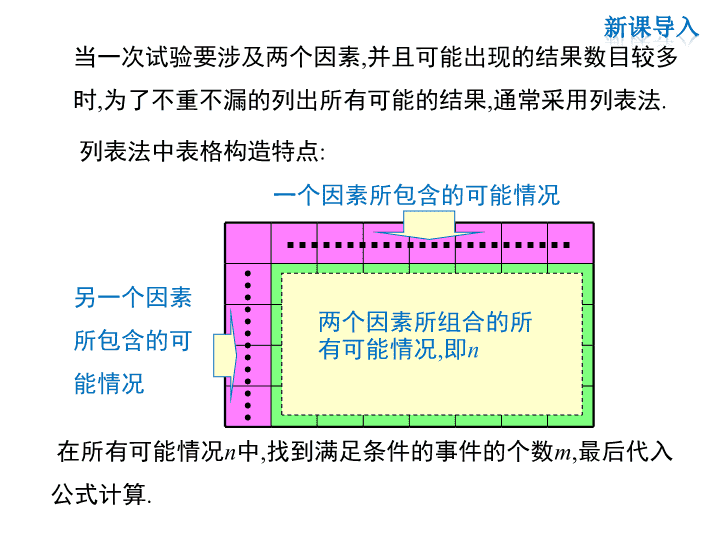
第25章 随机事件的概率 25.2 随机事件的概率 第3课时 列举所有机会均等的结果 问题2 什么时候用“列表法”方便?什么时候用“画树状图 法” 方便? 问题1 如何用“列表法”“画树状图法”求随机事件的概 率? 回顾与思考 当一次试验要涉及两个因素,并且可能出现的结果数目较多 时,为了不重不漏的列出所有可能的结果,通常采用列表法. 一个因素所包含的可能情况 另一个因素 所包含的可 能情况 两个因素所组合的所 有可能情况,即n 在所有可能情况n中,找到满足条件的事件的个数m,最后代入 公式计算. 列表法中表格构造特点: 当一次试验中涉及3个因素或更多的因素时,用列表法就不 方便了.为了不重不漏地列出所有可能的结果,通常采用画 树状图法. 一个试验 第一个因素 第二个因素 第三个因素 A B 1 2 3 1 2 3 a b a b a b a b a b a b n=2×3×2=12 抛掷一枚普通硬币3次.有人说“连续掷出三个正面”和 “先掷出两个正面,再掷出一个反面”的概率是一样的.你同意 吗? 正 反 正 反 正 反 正 反 正 反 正 反 正 反第1次 第2次 第3次 解: 每次抛掷,出现正面或反面的概率都相等, 画出树状图如下: 1 用画树状图法或列表法求概率 例1 由树状图可以看出,抛掷一枚普通硬币3次,共有以下8种机 会均等的结果: 正正正,正正反,正反正,正反反, 反正正,反正反,反反正,反反反. P(正正正)=P(正正反)= ,所以,题中的说法正确. 思考 有的同学认为:抛掷三枚普通硬币,硬币落地后只可能 出现4种结果:(1)全是正面;(2)两正一反;(3)两反 一正;(4)全是反面. 因此这四个事件出现的概率相等.你同意这种说法吗?为什么? 1 8 在6张卡片上分别写有1~6的整数,随机地抽取一张 后放回,再随机地抽取一张,那么第二次取出的数字能够 整除第一次取出的数字的概率是多少? 分析 问题中涉及两步,每一步都有6种不同的情况,此 时如果用树状图来表示所有可能的结果,就没有用表格 来表示简明. 例2 1 2 3 4 5 6 1 2 3 4 5 6 第一次 第二次 列表如下: (1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (2,1) (2,2) (2,3) (2,4) (2,5) (2,6) (3,1) (3,2) (3,3) (3,4) (3,5) (3,6) (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) (5,1) (5,2) (5,3) (5,4) (5,5) (5,6) (6,1) (6,2) (6,3) (6,4) (6,5) (6,6) 14 7 36 18 1.甲口袋中装有2个小球,1个红球、1个白球;乙口袋中装有3个小 球,1个红球、1个 白球、1个黑球;丙口袋中装有2个小球,1个红 球、1个黑球,这些小球除颜色外其余均相同.从3个口袋中各随 机地取出1个小球.求下列事件的概率: (1)取出的3个小球颜色均不同; (2)取出的3个小球有两个颜色相同; (3)取出的3个小球颜色全部相同. 由树形图可以看出,所有可能的结果有12种,它们出现的可 能性相等. (1) P(颜色均不相同) = (2) P(有两个颜色相同) = (3) P(颜色全部相同) = 解:画树状图如下: 甲 乙 丙 白 红 白 红 白 黑 红 黑红 黑红 黑红 黑红 黑红 黑 3 1 .12 4 8 2 .12 3 1 .12 红 黑 2.甲、乙两人玩掷骰子游戏,规定两人分别抛掷一枚骰子, 向上的点数之和为奇数,则甲获胜;向上的点数之和为偶数, 则乙获胜.你认为这个游戏的规则公平吗?为什么? 1 2 3 4 5 6 1 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 8 9 10 5 6 7 8 9 10 11 6 7 8 9 10 11 12 解:列表如下: 甲 乙和 由表可知,一共有36种等可能结果,其中和为奇数的有18 种,和为偶数的有18种,所以P(甲获胜)= P(乙获 胜)= 因为P(甲获胜)=P(乙获胜),所以游戏公平. 18 1 ,36 2 18 1 .36 2 ★1.列表法和画树状图法的优点: 当试验包含两步时,列表法比较方便,当然,此时也可以用 树状图法;当试验包含三步或三步以上时,用画树状图法 比较方便. ★2.列表法与画树状图法的选择: 利用树状图或表格可以清晰地表示出某个事件发生 的所有可能出现的结果;从而较方便地求出某些事件发生 的概率.查看更多