贵州省遵义市南白中学2020届高三第六次联考数学（理）试题

贵州省遵义市南白中学2020届高三第六次联考数学（理）试题

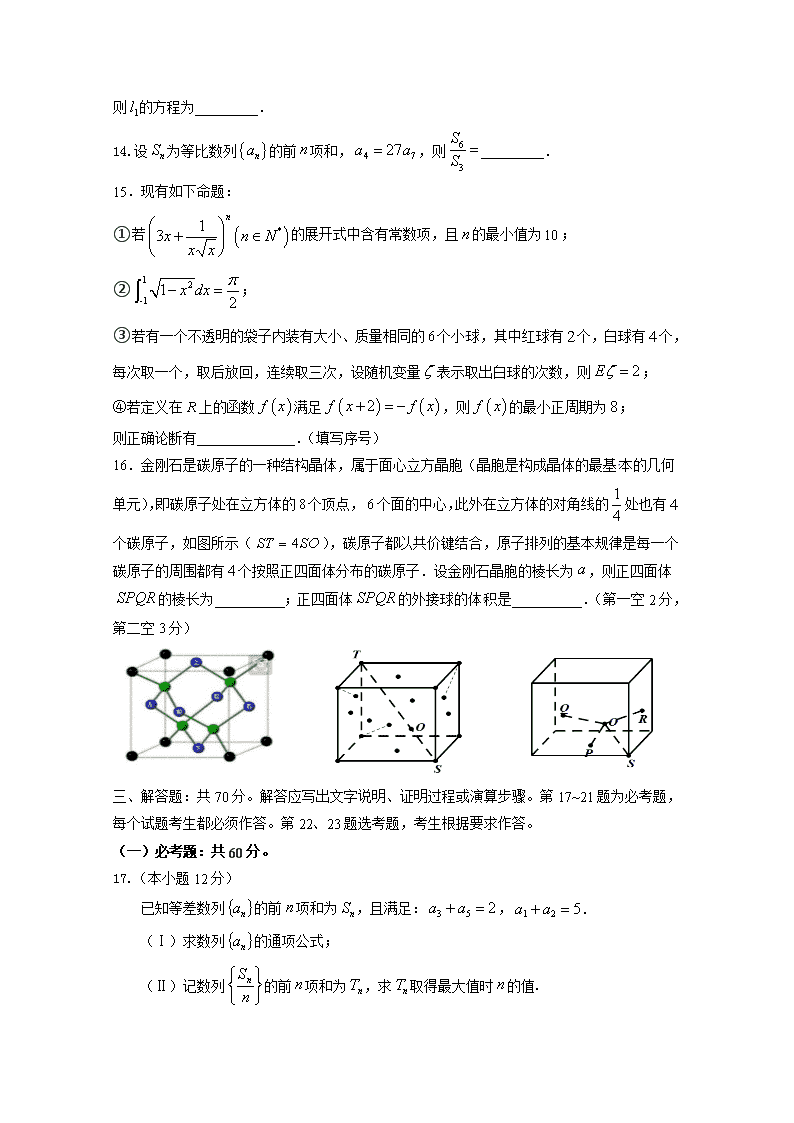
绝密★启用前 ‎2020年普通高等学校招生全国统一模拟考试（课标全国Ⅲ卷）‎ 理 科 数 学 注意事项：‎ ‎1.本卷满分150分，考试时间120分钟。答题前，现将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。‎ ‎2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。写在试题卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎3.非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎4.考试结束后，请将本试题卷和答题卡一并上交。‎ 第Ⅰ卷 ‎ 一、选择题：本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1.设集合，，则 A. B. C. D.‎ ‎2.在复平面内，已知复数对应的点与复数对应的点关于实轴对称，则 A. B. C. D.‎ ‎3.双曲线的焦点到渐近线的距离是 A. B. C. D.‎ ‎4.已知，则 A. B. C. D.‎ ‎5.把函数图象上各点的横坐标伸长为原来的倍，纵坐标不变，再将图象向右平移个单位，那么所得图象的一个对称中心为 A． B． C． D．‎ ‎6.已知函数,若，则的取值范围是 ‎ ‎ A． B． C． D． [来源:学科网ZXXK]‎ ‎7.在中，，则 ‎ A. B. C. D.‎ ‎8.设，，为锐角内角，，的对边，且满足，若，则的面积的最大值为 A. B. C. D.‎ ‎9.4名高三学生准备高考后到上海市、江苏省、浙江省、安徽省四个地方旅游， 假设每名同学均从这四个地方中任意选取一个去旅游， 则恰有一个地方未被选中的方法种类为 A． B． C． D．‎ ‎10.设正方体的棱长为，为的中点，为直线上一点，为平面内一点，则，两点间距离的最小值为 A． B． C． D．‎ ‎11.已知函数（，）在区间内有唯一零点，则的最大值为 A. B. C. D.‎ ‎12．已知双曲线的左、右顶点分别为.点为双曲线的左焦点，过点作垂直于轴的直线分别在第二、第三象限交双曲线于、两点，连接交轴于点，连接交 于点，且，则双曲线的离心率为 ‎ A. B.2 C.3 D.5‎ 第Ⅱ卷 二、填空题：本题共4个小题，每小题5分，共20分．‎ ‎13．已知圆：，斜率为的直线过定点且与圆相切，‎ 则的方程为_________．‎ ‎14.设为等比数列的前项和，，则_________．‎ ‎15．现有如下命题：‎ ‎①若的展开式中含有常数项，且的最小值为；‎ ‎②；‎ ‎③若有一个不透明的袋子内装有大小、质量相同的个小球，其中红球有个，白球有个，每次取一个，取后放回，连续取三次，设随机变量表示取出白球的次数，则；‎ ‎④若定义在R上的函数满足，则的最小正周期为；‎ 则正确论断有______________．（填写序号）‎ ‎16．金刚石是碳原子的一种结构晶体，属于面心立方晶胞（晶胞是构成晶体的最基本的几何单元），即碳原子处在立方体的个顶点，个面的中心，此外在立方体的对角线的处也有个碳原子，如图所示（），碳原子都以共价键结合，原子排列的基本规律是每一个碳原子的周围都有个按照正四面体分布的碳原子．设金刚石晶胞的棱长为，则正四面体的棱长为__________；正四面体的外接球的体积是__________．（第一空2分，第二空3分）‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题选考题，考生根据要求作答。‎ ‎（一）必考题：共60分。‎ ‎17.（本小题12分）‎ 已知等差数列的前项和为，且满足：，.‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）记数列的前项和为，求取得最大值时的值.‎ ‎18.（本小题12分）‎ 如图，正方形的边长为，以为折痕把折起，使点到达点的位置，且.‎ ‎（Ⅰ）证明：平面平面；‎ ‎（Ⅱ）若是的中点，，求二面角的余弦值.‎ ‎19.（本小题12分）‎ 指数是用体重公斤数除以身高米数的平方得出的数字，是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言，当数值大于或等于20.5时，我们说体重较重，当数值小于20.5时，我们说体重较轻，身高大于或等于我们说身高较高，身高小于170cm我们说身高较矮.‎ ‎（Ⅰ）已知某高中共有32名男体育特长生，其身高与指数的数据如散点图，请根据所得信息，完成下述列联表，并判断是否有的把握认为男生的身高对指数有影响.‎ 身高较矮 身高较高 合计 体重较轻 体重较重 合计 ‎（Ⅱ）①从上述32名男体育特长生中随机选取8名，其身高和体重的数据如表所示：‎ 编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 身高 ‎166‎ ‎167‎ ‎160‎ ‎173‎ ‎178‎ ‎169‎ ‎158‎ ‎173‎ 体重 ‎57‎ ‎58‎ ‎53‎ ‎61‎ ‎66‎ ‎57‎ ‎50‎ ‎66‎ 根据最小二乘法的思想与公式求得线性回归方程为.利用已经求得的线性回归方程，请完善下列残差表，并求（解释变量（身高）对于预报变量（体重）变化的贡献值）（保留两位有效数字）；‎ 编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 体重（）‎ ‎57‎ ‎58‎ ‎53‎ ‎61‎ ‎66‎ ‎57‎ ‎50‎ ‎66‎ 残差 ‎②通过残差分析，对于残差的最大（绝对值）的那组数据，需要确认在样本点的采集中是否有人为的错误，已知通过重新采集发现，该组数据的体重应该为.小明重新根据最最小二乘法的思想与公式，已算出，请在小明所算的基础上求出男体育特长生的身高与体重的线性回归方程.‎ 参考数据：‎ ‎，，，，‎ ‎0.10‎ ‎0.05[来源:学.科.网Z.X.X.K]‎ ‎0.01‎ ‎0.005‎ ‎2.706‎ ‎3.811‎ ‎6.635‎ ‎7.879‎ 参考公式：，，，，.‎ ‎20.（本小题12分）‎ 已知函数（，）.‎ ‎（Ⅰ）若，且在内有且只有一个零点，求的值；‎ ‎（Ⅱ）若，且有三个不同零点，问是否存在实数使得这三个零点成等差数列？若存在，求出的值，若不存在，请说明理由.‎ ‎21.（本小题12分）‎ 已知在上任意一点处的切线为，若过右焦点的直线交椭圆于两点，已知在点处切线相交于．‎ ‎（Ⅰ）求点的轨迹方程；‎ ‎（Ⅱ）①若过点且与直线垂直的直线（斜率存在且不为零）交椭圆于两点，证明为定值．‎ ‎②四边形的面积是否有最小值，若有请求出最小值；若没有请说明理由．‎ ‎（二）选考题：共10分。选考题：请考生在第22、23两题中任选一题作答。如果多做，则按所做的第一题积分。‎ ‎22.（本小题10分）选修4-4：坐标系与参数方程 ‎ 在平面直角坐标系中，曲线的参数方程为（为参数），以原点为极点，轴的非负半轴为极轴，建立极坐标系，曲线的极坐标方程为.‎ ‎（Ⅰ）求曲线的极坐标方程以及曲线的直角坐标方程；‎ ‎（Ⅱ）若直线与曲线、曲线在第一象限交于、两点，且，点的坐标为，求的面积.‎ ‎23.（本小题10分）选修4-5：不等式选讲 ‎ 已知函数.‎ ‎（Ⅰ）解不等式；‎ ‎（Ⅱ）若，，，求证：.‎ ‎2020年普通高等学校招生全国统一模拟考试（课标全国Ⅲ卷）答案 文 科 数 学 ‎ 一、选择题 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ C B A D D C A B A C A D 二、 填空题 ‎13‎ ‎14‎ ‎15‎ ‎16‎ 第一空；第二空：‎ ‎（第一空2分，第二空3分）‎ 三、 解答题 ‎17.解：‎ ‎（Ⅰ）设等差数列公差为，依题意，解之得.‎ ‎......4分 则.‎ 故数列的通项公式为（）. [来源:Zxxk.Com]‎ ‎......6分 ‎（Ⅱ）由得.数列为等差数列.‎ ‎......8分 由，所以，即，由于，故.‎ 故取得最大值时的值为. ‎ ‎ ......12分 ‎18.解：‎ ‎（Ⅰ）取中点，连结.‎ 因为，所以.‎ ‎......1分 在中，，，‎ 则，‎ 所以，‎ ‎......3分 又，且面，‎ 所以面，‎ ‎......5分 又面，所以面面.‎ ‎......6分 ‎（Ⅱ）因为面面，‎ 又面面，且，‎ 所以面，‎ ‎......8分 所以.‎ 又因为，，‎ 所以.‎ 因为，所以.‎ 又，‎ 所以，得.‎ ‎......12分 ‎19.解：‎ ‎（Ⅰ）设直线为，，易得在点处切线为，在点处切线为，由得又可得，‎ 点的轨迹方程；‎ ‎......6分[来源:Z_xx_k.Com]‎ ‎（Ⅱ）①设点、，设直线的方程为.‎ 将直线的方程与椭圆的方程联立，消去得.‎ 由韦达定理得，.‎ ‎......8分 所以=；‎ ‎......9分 由题意可得.‎ ‎......10分 ‎.‎ ‎......12分 ‎20.解：‎ ‎（Ⅰ）‎ 身高较矮 身高较高 合计 体重较轻 ‎6‎ ‎15‎ ‎21‎ 体重较重 ‎6‎ ‎5‎ ‎11‎ 合计 ‎12‎ ‎20‎ ‎32‎ 由于，‎ 因此没有的把握认为男生的身高对指数有影响. ‎ ‎......4分 ‎（Ⅱ）①对编号为8的数据，完成残差表如下所示：‎ 编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 体重 ‎57‎ ‎58‎ ‎53‎ ‎61[来源:Zxxk.Com]‎ ‎66‎ ‎57‎ ‎50‎ ‎66‎ 残差 ‎0.1‎ ‎0.3‎ ‎0.9‎ ‎3.5‎ ‎.‎ 所以解释变量（身高）对于预报变量（体重）变化的贡献值约为0.91. ‎ ‎......8分 ‎②由①可知，第八组数据的体重应为58.此时，易知，，，‎ ‎，‎ 所以重新采集数据后，男体育特长生的身高与体重的线性回归方程为.‎ ‎......12分 ‎21.解：‎ ‎（Ⅰ）若，则，.‎ ‎......2分 若，则函数在上单调递增,‎ ‎......3分 若，令，得，.‎ 在上，，单调递减，‎ 在上，，单调递增.‎ ‎......6分 ‎（Ⅱ）因为，则，若有三个不同零点，且成等差数列，‎ 可设,‎ 故，则，故，，.此时，，，故存在三个不同的零点，故符合题意的的值为.‎ ‎......12分 ‎22.解：‎ ‎（Ⅰ）依题意，曲线：，即，故.‎ ‎......2分 由得，即，即 ‎......4分 ‎（Ⅱ）设直线的极坐标方程为，分别代入曲线、的极坐标方程得，.‎ ‎......6分 由得，解得，则 ‎......8分 又，所以.‎ 故 ‎......10分 ‎23.解：‎ ‎（Ⅰ）.‎ ‎......3分 当时，解得；当时，无解；当时，解得.‎ 综上所述，不等式的解集为.‎ ‎......5分 ‎（Ⅱ）要证，即证，‎ 因为，，所以，，‎ ‎.‎ 所以，.故所证不等式成立.‎ ‎......10分