- 2021-05-10 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版数学七年级下册课件-第6章-6等式的性质与方程的简单变形
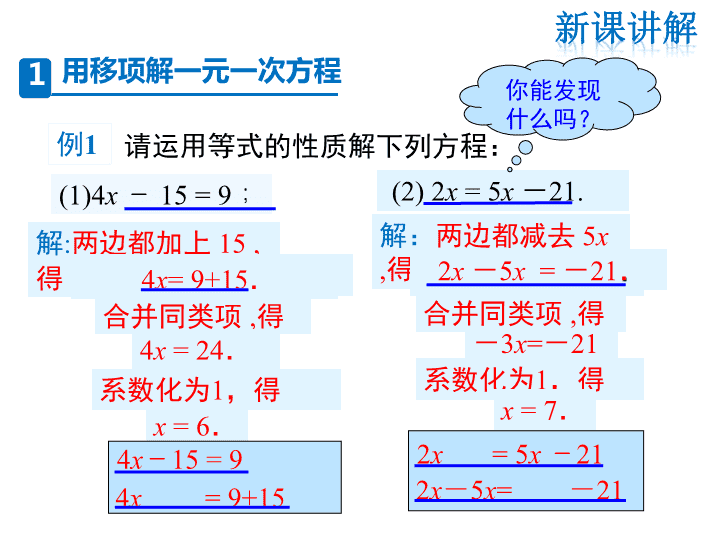
HS七(下) 教学课件 6.2.1 等式的性质与方程的简单变形 第6章 一元一次方程 第3课时 利用方程的变形求方程的解 (1)移项; 利用移项解方程的步骤: (3)系数化为1. (2)合并同类项; 请运用等式的性质解下列方程: (1)4x - 15 = 9; 解:两边都减去 5x , 得 -3x=- 21.系数化为1,得 x = 6. 解:两边都加上 15 , 得 系数化为1,得 x = 7. 合并同类项 ,得 合并同类项 ,得 4x = 24. 2x = 5x – 214x – 15 = 9 + 15 + 15 4x-15 = 9 4x = 9+15 2x-5x= -21 4x= 9+15. 你能发现 什么吗? 用移项解一元一次方程1 例1 4x -15 = 9 ① 4x = 9 + 15 ② 由方程① 到方程 ② , “– 15”这项移动后,发生了什么变化? 从方程的左边移到了方程的 右边. 改变了符号 4x-15 = 9 4x = 9+15 2x = 5x -21 ③ 2x -5x = -21 ④ 由方程③ 到方程 ④ , “ 5x ” 这项移动后,发生了什么变化? 改变了符号 从方程的右边移到了方程 的左边. 2x-5x= -21 解方程: .23273 xx 解:移项,得 合并同类项 ,得 3 2 32 7.x x 5 25.x 5.x 系数化为1,得 移项实际上是利 用等式的性质1, 但是解题步骤更 为简捷! 例2 (1) 8x=2x-7; (2) 6=8+2x; 解:移项,得 8x-2x=-7, 即 6x=-7. 两边同时除以6,得 解:原方程即 8+2x=6. 移项,得 2x=-2. 两边同时除以2,得 x=-1. 解方程: 7 . 6 x 例3 (3) 1 12 3. 2 2 y y 1 12 3 2 2 y y , 3 5 . 2 2 y 5 . 3 y 解:移项,得 即 两边都除以 ,得 3 2 练一练 解下列方程: (1) 2.5x+318 =1068; (2) 2.4y + 2y+2.4 = 6.8. x = 300 y = 1 (1)7 2 3 4x x (2)1.8 30 0.3t t 解下列一元一次方程: 5 4 11 8(4) 3 3 3 3 x x xx 31 2 1)3( 答案:(1) x=-2 (2) t=20 (3) x=-4 (4) x=2 解形如“ax+b=cx+d”的方程的一般步骤: (1)移项; (2)合并同类项; (3)化未知数的系数为1.查看更多