2019年陕西省中考数学试卷

2019年陕西省中考数学试卷

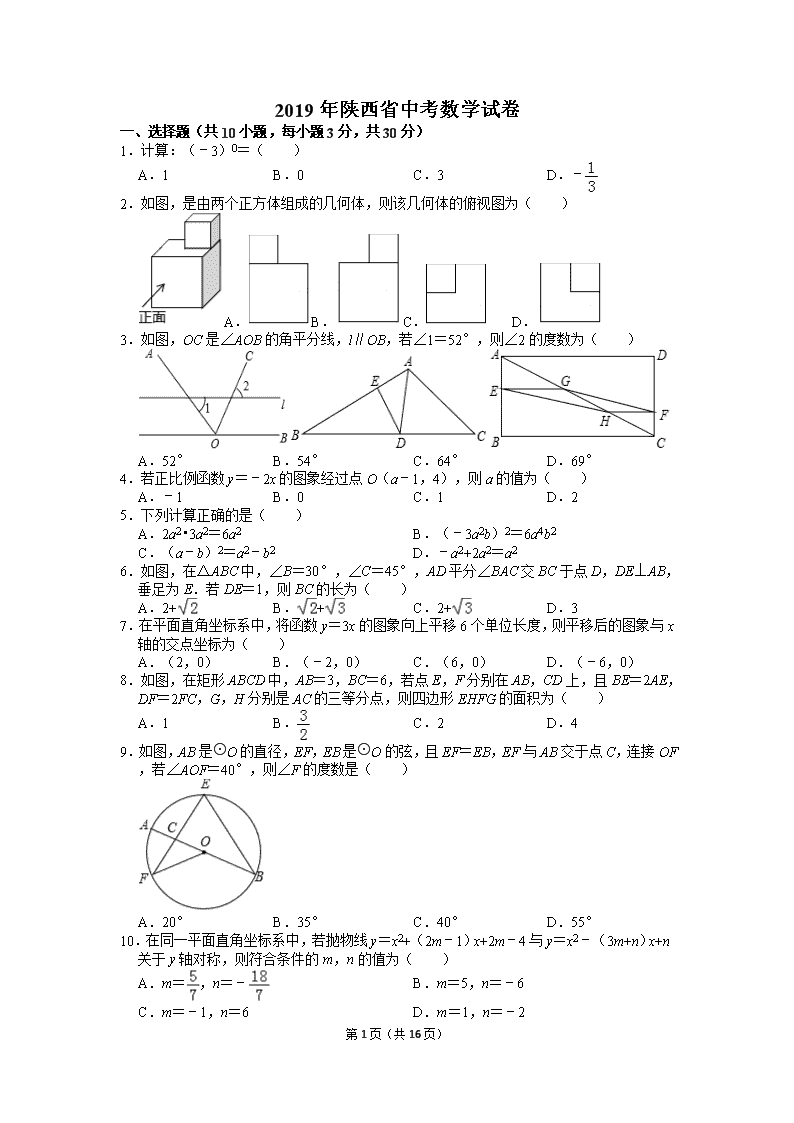
‎2019年陕西省中考数学试卷 一、选择题（共10小题，每小题3分，共30分）‎ ‎1．计算：（﹣3）0＝（　　）‎ A．1 B．0 C．3 D．﹣‎ ‎2．如图，是由两个正方体组成的几何体，则该几何体的俯视图为（　　）‎ A．B．C． D．‎ ‎3．如图，OC是∠AOB的角平分线，l∥OB，若∠1＝52°，则∠2的度数为（　　）‎ A．52° B．54° C．64° D．69°‎ ‎4．若正比例函数y＝﹣2x的图象经过点O（a﹣1，4），则a的值为（　　）‎ A．﹣1 B．0 C．1 D．2‎ ‎5．下列计算正确的是（　　）‎ A．2a2•3a2＝6a2 B．（﹣3a2b）2＝6a4b2 ‎ C．（a﹣b）2＝a2﹣b2 D．﹣a2+2a2＝a2‎ ‎6．如图，在△ABC中，∠B＝30°，∠C＝45°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E．若DE＝1，则BC的长为（　　）‎ A．2+ B．+ C．2+ D．3‎ ‎7．在平面直角坐标系中，将函数y＝3x的图象向上平移6个单位长度，则平移后的图象与x轴的交点坐标为（　　）‎ A．（2，0） B．（﹣2，0） C．（6，0） D．（﹣6，0）‎ ‎8．如图，在矩形ABCD中，AB＝3，BC＝6，若点E，F分别在AB，CD上，且BE＝2AE，DF＝2FC，G，H分别是AC的三等分点，则四边形EHFG的面积为（　　）‎ A．1 B． C．2 D．4‎ ‎9．如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF＝EB，EF与AB交于点C，连接OF，若∠AOF＝40°，则∠F的度数是（　　）‎ A．20° B．35° C．40° D．55°‎ ‎10．在同一平面直角坐标系中，若抛物线y＝x2+（2m﹣1）x+2m﹣4与y＝x2﹣（3m+n）x+n关于y轴对称，则符合条件的m，n的值为（　　）‎ A．m＝，n＝﹣ B．m＝5，n＝﹣6 ‎ C．m＝﹣1，n＝6 D．m＝1，n＝﹣2‎ 第16页（共16页）‎ 二、填空题（共4小题，每小题3分，共12分）‎ ‎11．已知实数﹣，0.16，，π，，，其中为无理数的是　 　．‎ ‎12．若正六边形的边长为3，则其较长的一条对角线长为　 　．‎ ‎13．如图，D是矩形AOBC的对称中心，A（0，4），B（6，0），若一个反比例函数的图象经过点D，交AC于点M，则点M的坐标为　 　．‎ ‎14．如图，在正方形ABCD中，AB＝8，AC与BD交于点O，N是AO的中点，点M在BC边上，且BM＝6．P为对角线BD上一点，则PM﹣PN的最大值为　 　．‎ 三、解答题（共78分）‎ ‎15.(5分)计算：﹣2×+|1﹣|﹣（）﹣2 ；16.(5分)化简：（+）÷‎ ‎17．（5分）如图，在△ABC中，AB＝AC，AD是BC边上的高．请用尺规作图法，求作△ABC的外接圆．（保留作图痕迹，不写作法）‎ ‎18．（5分）如图，点A，E，F在直线l上，AE＝BF，AC∥BD，且AC＝BD，求证：CF＝DE．‎ ‎19．（7分）本学期初，某校为迎接中华人民共和国建国七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代”为主题的读书活动．校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”（下面简称：“读书量”）进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，如图所示：‎ 第16页（共16页）‎ 根据以上信息，解答下列问题：‎ ‎（1）补全上面两幅统计图，填出本次所抽取学生四月份“读书量”的众数为　 　．‎ ‎（2）求本次所抽取学生四月份“读书量”的平均数；‎ ‎（3）已知该校七年级有1200名学生，请你估计该校七年级学生中，四月份“读书量”为5本的学生人数．‎ ‎20．（7分）小明利用刚学过的测量知识来测量学校内一棵古树的高度．一天下午，他和学习小组的同学带着测量工具来到这棵古树前，由于有围栏保护，他们无法到达古树的底部B，如图所示．于是他们先在古树周围的空地上选择一点D，并在点D处安装了测量器DC，测得古树的顶端A的仰角为45°；再在BD的延长线上确定一点G，使DG＝5米，并在G处的地面上水平放置了一个小平面镜，小明沿着BG方向移动，当移动带点F时，他刚好在小平面镜内看到这棵古树的顶端A的像，此时，测得FG＝2米，小明眼睛与地面的距离EF＝1.6米，测倾器的高度CD＝0.5米．已知点F、G、D、B在同一水平直线上，且EF、CD、AB均垂直于FB，求这棵古树的高度AB．（小平面镜的大小忽略不计）‎ ‎ ‎ ‎21．（7分）根据记录，从地面向上11km以内，每升高1km，气温降低6℃；又知在距离地面11km以上高空，气温几乎不变．若地面气温为m（℃），设距地面的高度为x（km）处的气温为y（℃）‎ ‎（1）写出距地面的高度在11km以内的y与x之间的函数表达式；‎ ‎（2）上周日，小敏在乘飞机从上海飞回西安途中，某一时刻，她从机舱内屏幕显示的相关数据得知，飞机外气温为﹣26℃时，飞机距离地面的高度为7km，求当时这架飞机下方地面的气温；小敏想，假如飞机当时在距离地面12km的高空，飞机外的气温是多少度呢？请求出假如当时飞机距离地面12km时，飞机外的气温．‎ ‎22．（7分）现有A、B两个不透明袋子，分别装有3个除颜色外完全相同的小球．其中，A袋装有2个白球，1个红球；B袋装有2个红球，1个白球．‎ ‎（1）将A袋摇匀，然后从A袋中随机取出一个小球，求摸出小球是白色的概率；‎ ‎（2）小华和小林商定了一个游戏规则：从摇匀后的A，B两袋中随机摸出一个小球，摸出的这两个小球，若颜色相同，则小林获胜；若颜色不同，则小华获胜．请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平．‎ ‎23．（8分）如图，AC是⊙O的一条弦，AP是⊙O的切线．作BM＝AB并与AP交于点M，延长MB交AC于点E，交⊙O于点D，连接AD．‎ ‎（1）求证：AB＝BE；‎ ‎（2）若⊙O的半径R＝5，AB＝6，求AD的长．‎ 第16页（共16页）‎ ‎ ‎ ‎24．（10分）在平面直角坐标系中，已知抛物线L：y＝ax2+（c﹣a）x+c经过点A（﹣3，0）和点B（0，﹣6），L关于原点O堆成的抛物线为L′．‎ ‎（1）求抛物线L的表达式；‎ ‎（2）点P在抛物线L′上，且位于第一象限，过点P作PD⊥y轴，垂足为D．若△POD与△AOB相似，求复合条件的点P的坐标．‎ ‎25．（12分）问题提出：‎ ‎（1）如图1，已知△ABC，试确定一点D，使得以A，B，C，D为顶点的四边形为平行四边形，请画出这个平行四边形；‎ 问题探究：‎ ‎（2）如图2，在矩形ABCD中，AB＝4，BC＝10，若要在该矩形中作出一个面积最大的△BPC，且使∠BPC＝90°，求满足条件的点P到点A的距离；‎ 问题解决：‎ ‎（3）如图3，有一座草根塔A，按规定，要以塔A为对称中心，建一个面积尽可能大的形状为平行四边形的草根景区BCDE．根据实际情况，要求顶点B是定点，点B到塔A的距离为50米，∠CBE＝120°，那么，是否可以建一个满足要求的面积最大的平行四边形景区BCDE？若可以，求出满足要求的平行四边形BCDE的最大面积；若不可以，请说明理由．（塔A的占地面积忽略不计）‎ 第16页（共16页）‎ ‎2019年陕西省中考数学试卷 参考答案与试题解析 一、选择题（共10小题，每小题3分，共30分）‎ ‎1．计算：（﹣3）0＝（　　）‎ A．1 B．0 C．3 D．﹣‎ ‎【解答】解：（﹣3）0＝1．‎ 故选：A．‎ ‎2．如图，是由两个正方体组成的几何体，则该几何体的俯视图为（　　）‎ A． B． C． D．‎ ‎【解答】解：从上往下看，所以小正方形应在大正方形的右上角．‎ 故选：D．‎ ‎3．如图，OC是∠AOB的角平分线，l∥OB，若∠1＝52°，则∠2的度数为（　　）‎ A．52° B．54° C．64° D．69°‎ ‎【解答】解：∵l∥OB，‎ ‎∴∠1+∠AOB＝180°，‎ ‎∴∠AOB＝128°，‎ ‎∵OC平分∠AOB，‎ ‎∴∠BOC＝64°，‎ 又l∥OB，且∠2与∠BOC为同位角，‎ ‎∴∠2＝64°，‎ 故选：C．‎ ‎4．若正比例函数y＝﹣2x的图象经过点O（a﹣1，4），则a的值为（　　）‎ A．﹣1 B．0 C．1 D．2‎ ‎【解答】解：∵正比例函数y＝﹣2x的图象经过点O（a﹣1，4），‎ ‎∴4＝﹣2（a﹣1），解得：a＝﹣1．‎ 故选：A．‎ ‎5．下列计算正确的是（　　）‎ A．2a2•3a2＝6a2 B．（﹣3a2b）2＝6a4b2 ‎ C．（a﹣b）2＝a2﹣b2 D．﹣a2+2a2＝a2‎ ‎【解答】解：∵2a2•3a2＝6a4，故选项A错误，‎ ‎∵（﹣3a2b）2＝9a4b2，故选项B错误，‎ ‎∵（a﹣b）2＝a2﹣2ab+b2，故选项C错误，‎ 第16页（共16页）‎ ‎∵﹣a2+2a2＝a2，故选项D正确，‎ 故选：D．‎ ‎6．如图，在△ABC中，∠B＝30°，∠C＝45°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E．若DE＝1，则BC的长为（　　）‎ A．2+ B．+ C．2+ D．3‎ ‎【解答】解：过点D作DF⊥AC于F如图所示，‎ ‎∵AD为∠BAC的平分线，且DE⊥AB于E，DF⊥AC于F，‎ ‎∴DE＝DF＝1，‎ 在Rt△BED中，∠B＝30°，‎ ‎∴BD＝2DE＝2，‎ 在Rt△CDF中，∠C＝45°，‎ ‎∴△CDF为等腰直角三角形，‎ ‎∴CD＝DF＝，‎ ‎∴BC＝BD+CD＝2，‎ 故选：A．‎ ‎7．在平面直角坐标系中，将函数y＝3x的图象向上平移6个单位长度，则平移后的图象与x轴的交点坐标为（　　）‎ A．（2，0） B．（﹣2，0） C．（6，0） D．（﹣6，0）‎ ‎【解答】解：由“上加下减”的原则可知，将函数y＝3x的图象向上平移6个单位长度所得函数的解析式为y＝3x+6，‎ ‎∵此时与x轴相交，则y＝0，‎ ‎∴3x+6＝0，即x＝﹣2，‎ ‎∴点坐标为（﹣2，0），‎ 故选：B．‎ ‎8．如图，在矩形ABCD中，AB＝3，BC＝6，若点E，F分别在AB，CD上，且BE＝2AE，DF＝2FC，G，H分别是AC的三等分点，则四边形EHFG的面积为（　　）‎ A．1 B． C．2 D．4‎ ‎【解答】解：∵BE＝2AE，DF＝2FC，∴，＝‎ ‎∵G、H分别是AC的三等分点 ‎∴，＝‎ ‎∴‎ 第16页（共16页）‎ ‎∴EG∥BC ‎∴，且BC＝6‎ ‎∴EG＝2，‎ 同理可得HF∥AD，HF＝2‎ ‎∴四边形EHFG为平行四边形，且EG和HF间距离为1‎ ‎∴S四边形EHFG＝2×1＝2，‎ 故选：C．‎ ‎9．如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF＝EB，EF与AB交于点C，连接OF，若∠AOF＝40°，则∠F的度数是（　　）‎ A．20° B．35° C．40° D．55°‎ ‎【解答】解：连接FB．‎ ‎∵∠AOF＝40°，‎ ‎∴∠FOB＝180°﹣40°＝140°，‎ ‎∴∠FEB＝∠FOB＝70°‎ ‎∵EF＝EB ‎∴∠EFB＝∠EBF＝55°，‎ ‎∵FO＝BO，‎ ‎∴∠OFB＝∠OBF＝20°，‎ ‎∴∠EFO＝∠EBO，‎ ‎∠EFO＝∠EFB﹣∠OFB＝35°，‎ 故选：B．‎ ‎10．在同一平面直角坐标系中，若抛物线y＝x2+（2m﹣1）x+2m﹣4与y＝x2﹣（3m+n）x+n关于y轴对称，则符合条件的m，n的值为（　　）‎ A．m＝，n＝﹣ B．m＝5，n＝﹣6 ‎ C．m＝﹣1，n＝6 D．m＝1，n＝﹣2‎ ‎【解答】解：∵抛物线y＝x2+（2m﹣1）x+2m﹣4与y＝x2﹣（3m+n）x+n关于y轴对称，‎ ‎∴，解之得，‎ 故选：D．‎ 二、填空题（共4小题，每小题3分，共12分）‎ ‎11．已知实数﹣，0.16，，π，，，其中为无理数的是　，π，　．‎ 第16页（共16页）‎ ‎【解答】解：，、0.16是有理数；‎ 无理数有、π、．‎ 故答案为：、π、．‎ ‎12．若正六边形的边长为3，则其较长的一条对角线长为　6　．‎ ‎【解答】解：如图所示为正六边形最长的三条对角线，‎ 由正六边形性质可知，△AOB，△COD为两个边长相等的等边三角形，‎ ‎∴AD＝2AB＝6，‎ 故答案为6．‎ ‎13．如图，D是矩形AOBC的对称中心，A（0，4），B（6，0），若一个反比例函数的图象经过点D，交AC于点M，则点M的坐标为　（，4）　．‎ ‎【解答】解：∵A（0，4），B（6，0），‎ ‎∴C（6，4），‎ ‎∵D是矩形AOBC的对称中心，‎ ‎∴D（3，2），‎ 设反比例函数的解析式为y＝，‎ ‎∴k＝3×2＝6，‎ ‎∴反比例函数的解析式为y＝，‎ 把y＝4代入得4＝，解得x＝，‎ 故M的坐标为（，4）．‎ 故答案为（，4）．‎ ‎14．如图，在正方形ABCD中，AB＝8，AC与BD交于点O，N是AO的中点，点M在BC边上，且BM＝6．P为对角线BD上一点，则PM﹣PN的最大值为　2　．‎ ‎【解答】解：如图所示，作以BD为对称轴作N的对称点N'，连接PN'，MN'，‎ 根据轴对称性质可知，PN＝PN'，‎ 第16页（共16页）‎ ‎∴PM﹣PN＝PM﹣PN'≤MN'，‎ 当P，M，N'三点共线时，取“＝”，‎ ‎∵正方形边长为8，‎ ‎∴AC＝AB＝，‎ ‎∵O为AC中点，‎ ‎∴AO＝OC＝，‎ ‎∵N为OA中点，‎ ‎∴ON＝，‎ ‎∴ON'＝CN'＝，‎ ‎∴AN'＝，‎ ‎∵BM＝6，‎ ‎∴CM＝AB﹣BM＝8﹣6＝2，‎ ‎∴＝＝‎ ‎∴PM∥AB∥CD，∠CMN'＝90°，‎ ‎∵∠N'CM＝45°，‎ ‎∴△N'CM为等腰直角三角形，‎ ‎∴CM＝MN'＝2，‎ 即PM﹣PN的最大值为2，‎ 故答案为：2．‎ 三、解答题（共78分）‎ ‎15．（5分）计算：﹣2×+|1﹣|﹣（）﹣2‎ ‎【解答】解：原式＝﹣2×（﹣3）+﹣1﹣4‎ ‎＝1+．‎ ‎16．（5分）化简：（+）÷‎ ‎【解答】解：原式＝[•‎ ‎＝•‎ ‎＝a．‎ ‎17．（5分）如图，在△ABC中，AB＝AC，AD是BC边上的高．请用尺规作图法，求作△ABC的外接圆．（保留作图痕迹，不写作法）‎ 第16页（共16页）‎ ‎【解答】解：如图所示：⊙O即为所求．‎ ‎18．（5分）如图，点A，E，F在直线l上，AE＝BF，AC∥BD，且AC＝BD，求证：CF＝DE．‎ ‎【解答】证明：∵AE＝BF，‎ ‎∴AE+EF＝BF+EF，即AF＝BE，‎ ‎∵AC∥BD，‎ ‎∴∠CAF＝∠DBE，‎ 在△ACF和△BDE中，‎ ‎，‎ ‎∴△ACF≌△BDE（SAS）‎ ‎∴CF＝DE．‎ ‎19．（7分）本学期初，某校为迎接中华人民共和国建国七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代”为主题的读书活动．校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”（下面简称：“读书量”）进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，如图所示：‎ 第16页（共16页）‎ 根据以上信息，解答下列问题：‎ ‎（1）补全上面两幅统计图，填出本次所抽取学生四月份“读书量”的众数为　3　．‎ ‎（2）求本次所抽取学生四月份“读书量”的平均数；‎ ‎（3）已知该校七年级有1200名学生，请你估计该校七年级学生中，四月份“读书量”为5本的学生人数．‎ ‎【解答】解：（1）根据统计图可知众数为3，‎ 故答案为3；‎ ‎（2）平均数＝；‎ ‎（3）四月份“读书量”为5本的学生人数＝1200×＝120（人），‎ 答：四月份“读书量”为5本的学生人数为120人．‎ ‎20．（7分）小明利用刚学过的测量知识来测量学校内一棵古树的高度．一天下午，他和学习小组的同学带着测量工具来到这棵古树前，由于有围栏保护，他们无法到达古树的底部B，如图所示．于是他们先在古树周围的空地上选择一点D，并在点D处安装了测量器DC，测得古树的顶端A的仰角为45°；再在BD的延长线上确定一点G，使DG＝5米，并在G处的地面上水平放置了一个小平面镜，小明沿着BG方向移动，当移动带点F时，他刚好在小平面镜内看到这棵古树的顶端A的像，此时，测得FG＝2米，小明眼睛与地面的距离EF＝1.6米，测倾器的高度CD＝0.5米．已知点F、G、D、B在同一水平直线上，且EF、CD、AB均垂直于FB，求这棵古树的高度AB．（小平面镜的大小忽略不计）‎ 第16页（共16页）‎ ‎【解答】解：如图，过点C作CH⊥AB于点H，‎ 则CH＝BD，BH＝CD＝0.5．‎ 在Rt△ACH中，∠ACH＝45°，‎ ‎∴AH＝CH＝BD，‎ ‎∴AB＝AH+BH＝BD+0.5．‎ ‎∵EF⊥FB，AB⊥FB，‎ ‎∴∠EFG＝∠ABG＝90°．‎ 由题意，易知∠EGF＝∠AGB，‎ ‎∴△EFG∽△ABG，‎ ‎∴＝即＝，‎ 解之，得BD＝17.5，‎ ‎∴AB＝17.5+0.5＝18（m）．‎ ‎∴这棵古树的高AB为18m．‎ ‎21．（7分）根据记录，从地面向上11km以内，每升高1km，气温降低6℃；又知在距离地面11km以上高空，气温几乎不变．若地面气温为m（℃），设距地面的高度为x（km）处的气温为y（℃）‎ ‎（1）写出距地面的高度在11km以内的y与x之间的函数表达式；‎ ‎（2）上周日，小敏在乘飞机从上海飞回西安途中，某一时刻，她从机舱内屏幕显示的相关数据得知，飞机外气温为﹣26℃时，飞机距离地面的高度为7km，求当时这架飞机下方地面的气温；小敏想，假如飞机当时在距离地面12km的高空，飞机外的气温是多少度呢？请求出假如当时飞机距离地面12km时，飞机外的气温．‎ ‎【解答】解：（1）根据题意得：y＝m﹣6x；‎ ‎（2）将x＝7，y＝﹣26代入y＝m﹣6x，得﹣26＝m﹣42，∴m＝16‎ ‎∴当时地面气温为16℃‎ ‎∵x＝12＞11，‎ ‎∴y＝16﹣6×11＝﹣50（℃）‎ 假如当时飞机距地面12km时，飞机外的气温为﹣50℃．‎ ‎22．（7分）现有A、B两个不透明袋子，分别装有3个除颜色外完全相同的小球．其中，A袋装有2个白球，1个红球；B袋装有2个红球，1个白球．‎ ‎（1）将A袋摇匀，然后从A袋中随机取出一个小球，求摸出小球是白色的概率；‎ ‎（2）小华和小林商定了一个游戏规则：从摇匀后的A，B两袋中随机摸出一个小球，摸出的这两个小球，若颜色相同，则小林获胜；若颜色不同，则小华获胜．请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平．‎ ‎【解答】解：（1）共有3种等可能结果，而摸出白球的结果有2种 ‎∴P（摸出白球）＝；‎ ‎（2）根据题意，列表如下：‎ A B ‎ 红1‎ 红2‎ 白 白1‎ ‎（白1，红1）‎ ‎（白1，红2）‎ ‎（白1，白）‎ 白2‎ ‎（白2，红1）‎ ‎（白2，红2）‎ ‎（白2，白）‎ 红 ‎（红，红1）‎ ‎（红，红2）‎ ‎（白1，白）‎ 第16页（共16页）‎ 由上表可知，共有9种等可能结果，其中颜色不相同的结果有4种，颜色相同的结果有5种 ‎∴P（颜色不相同）＝，P（颜色相同）＝‎ ‎∵＜‎ ‎∴这个游戏规则对双方不公平 ‎23．（8分）如图，AC是⊙O的一条弦，AP是⊙O的切线．作BM＝AB并与AP交于点M，延长MB交AC于点E，交⊙O于点D，连接AD．‎ ‎（1）求证：AB＝BE；‎ ‎（2）若⊙O的半径R＝5，AB＝6，求AD的长．‎ ‎【解答】（1）证明：∵AP是⊙O的切线，‎ ‎∴∠EAM＝90°，‎ ‎∴∠BAE+∠MAB＝90°，∠AEB+∠AMB＝90°．‎ 又∵AB＝BM，‎ ‎∴∠MAB＝∠AMB，‎ ‎∴∠BAE＝∠AEB，‎ ‎∴AB＝BE ‎（2）解：连接BC ‎∵AC是⊙O的直径，‎ ‎∴∠ABC＝90°‎ 在Rt△ABC中，AC＝10，AB＝6，‎ ‎∴BC＝8，‎ ‎∵BE＝AB＝BM，‎ ‎∴EM＝12，‎ 由（1）知，∠BAE＝∠AEB，‎ ‎∴△ABC∽△EAM ‎∴∠C＝∠AME，＝，‎ 即＝，‎ ‎∴AM＝‎ 又∵∠D＝∠C，‎ ‎∴∠D＝∠AMD ‎∴AD＝AM＝．‎ 第16页（共16页）‎ ‎24．（10分）在平面直角坐标系中，已知抛物线L：y＝ax2+（c﹣a）x+c经过点A（﹣3，0）和点B（0，﹣6），L关于原点O堆成的抛物线为L′．‎ ‎（1）求抛物线L的表达式；‎ ‎（2）点P在抛物线L′上，且位于第一象限，过点P作PD⊥y轴，垂足为D．若△POD与△AOB相似，求复合条件的点P的坐标．‎ ‎【解答】解：（1）将点A、B的坐标代入抛物线表达式得：，解得：，‎ ‎∴L：y＝x2﹣5x﹣6‎ ‎（2）∵点A、B在L′上的对应点分别为A′（﹣3，0）、B′（0，﹣6），‎ ‎∴设抛物线L′的表达式y＝x2+bx+6，‎ 将A′（﹣3，0）代入y＝x2+bx+6，得b＝﹣5，‎ ‎∴抛物线L′的表达式为y＝x2﹣5x+6，‎ A（﹣3，0），B（0，﹣6），‎ ‎∴AO＝3，OB＝6，‎ 设：P（m，m2﹣5m+6）（m＞0），‎ ‎∵PD⊥y轴，‎ ‎∴点D的坐标为（0，m2﹣5m+6），‎ ‎∵PD＝m，OD＝m2﹣5m+6，‎ Rt△POD与Rt△AOB相似，‎ ‎①△POD∽△BOA时，‎ ‎，即m＝2（m2﹣5m+6），‎ 解得：m＝或4；‎ ‎②当△OPD∽△AOB时，‎ 同理可得：m＝1或6；‎ 第16页（共16页）‎ ‎∵P1、P2、P3、P4均在第一象限，‎ ‎∴符合条件的点P的坐标为（1，2）或（6，12）或（23，43）或（4，2）．‎ ‎25．（12分）问题提出：‎ ‎（1）如图1，已知△ABC，试确定一点D，使得以A，B，C，D为顶点的四边形为平行四边形，请画出这个平行四边形；‎ 问题探究：‎ ‎（2）如图2，在矩形ABCD中，AB＝4，BC＝10，若要在该矩形中作出一个面积最大的△BPC，且使∠BPC＝90°，求满足条件的点P到点A的距离；‎ 问题解决：‎ ‎（3）如图3，有一座草根塔A，按规定，要以塔A为对称中心，建一个面积尽可能大的形状为平行四边形的草根景区BCDE．根据实际情况，要求顶点B是定点，点B到塔A的距离为50米，∠CBE＝120°，那么，是否可以建一个满足要求的面积最大的平行四边形景区BCDE？若可以，求出满足要求的平行四边形BCDE的最大面积；若不可以，请说明理由．（塔A的占地面积忽略不计）‎ ‎【解答】解：（1）如图记为点D所在的位置．‎ ‎（2）如图，‎ ‎∵AB＝4，BC＝10，∴取BC的中点O，则OB＞AB．‎ ‎∴以点O为圆心，OB长为半径作⊙O，⊙O一定于AD相交于P1，P2两点，‎ 连接BP1，P1C，P1O，∵∠BPC＝90°，点P不能再矩形外；‎ ‎∴△BPC的顶点P1或P2位置时，△BPC的面积最大，‎ 作P1E⊥BC，垂足为E，则OE＝3，‎ ‎∴AP1＝BE＝OB﹣OE＝5﹣3＝2，‎ 由对称性得AP2＝8．‎ ‎（3）可以，如图所示，连接BD，‎ 第16页（共16页）‎ ‎∵A为▱BCDE的对称中心，BA＝50，∠CBE＝120°，‎ ‎∴BD＝100，∠BED＝60°‎ 作△BDE的外接圆⊙O，则点E在优弧上，取的中点E′，连接E′B，E′D，‎ 则E′B＝E′D，且∠BE′D＝60°，∴△BE′D为正三角形．‎ 连接E′O并延长，经过点A至C′，使E′A＝AC′，连接BC′，DC′，‎ ‎∵E′A⊥BD，‎ ‎∴四边形E′D为菱形，且∠C′BE′＝120°，‎ 作EF⊥BD，垂足为F，连接EO，则EF≤EO+OA﹣E′O+OA＝E′A，‎ ‎∴S△BDE＝•BD•EF≤•BD•E′A＝S△E′BD，‎ ‎∴S平行四边形BCDE≤S平行四边形BC′DE′＝2S△E′BD＝1002•sin60°＝5000（m2）‎ 所以符合要求的▱BCDE的最大面积为5000m2．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/7/12 9:27:16；用户：柯瑞；邮箱：ainixiaoke00@163.com；学号：500557‎ 第16页（共16页）‎