2014湖南省永州市中考数学试卷

2014湖南省永州市中考数学试卷

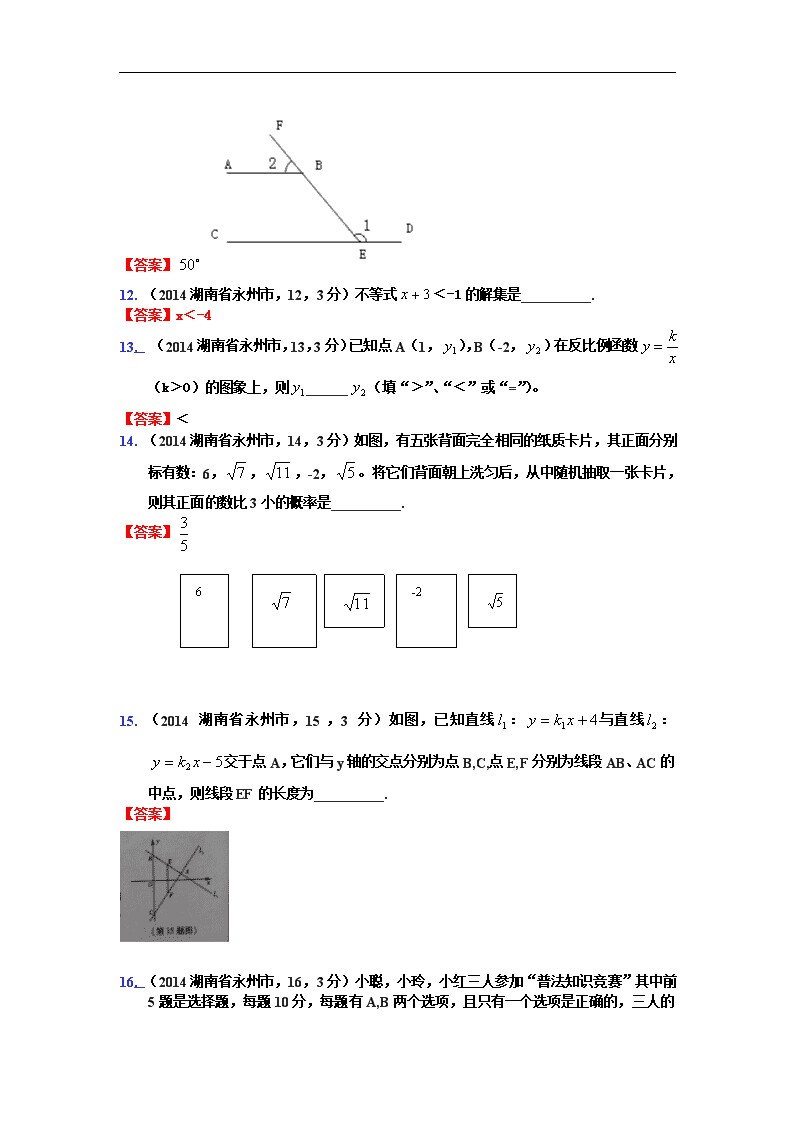
‎2014年湖南省永州市中考数学试卷 ‎（满分120分，考试时间120分钟）‎ 一、选择题（本大题共8个小题，每小题3分，满分24分，每小题只有一个正确答案，请将正确选项填涂到答题卡上。）‎ ‎1.（2014湖南省永州市，1，3分）据统计我国2014年前四月已开工建造286万套保障房，其中286万用科学记数法表示为（ ）‎ ‎ A. B. C. D.‎ ‎【答案】A ‎2. （2014湖南省永州市，2，3分）永州的文化底蕴深厚，永州人民的生活健康向上，如瑶族长鼓舞，东安武术，宁远举重等，下面的四幅简笔画是从永州的文化活动中抽象出来的，其中是轴对称图形的是（ ）‎ A.B.C.D.‎ ‎【答案】C ‎3. （2014湖南省永州市，3，3分）下列运算正确的是（ ）‎ A. B.‎ C. D.‎ ‎【答案】D ‎4. （2014湖南省永州市，4，3分）某校7名初中男生参加引体向上体育测试的成绩分别为：8，5，7，5，8，6，8，则这组数据的众数和中位数分别为（ ）‎ A.6，7 B.8，7 C.8，6 D.5，7‎ ‎【答案】B ‎5. （2014湖南省永州市，5，3分）若运用湘教版初中数学教材上使用的某种电子计算器进行计算，则按键：‎ 的结果为（ ）‎ A.21 B.15 C.84 D.67‎ ‎【答案】‎ ‎6. （2014湖南省永州市，6，3分）下列命题是假命题的是（ ）‎ A.不在同一直线上的三点确定一个圆 B.矩形的对角线互相垂直平分 C.正六边形的内角和是 D.角平分线上的点到角两边的距离相等 ‎【答案】B ‎7. （2014湖南省永州市，7，3分）若某几何体的三视图如图所示，则这个几何体是（ ）‎ ‎. ‎ ‎【答案】C ‎8. jscm（2014湖南省永州市，8，3分）在求的值时，小林发现：从第二个加数起每一个加数都是前一个加数的6倍，于是她设： ①， ‎ 然后在①式的两边都乘以6，得：‎ ‎ ②，‎ ‎ ②-①得，即，所以。得出答案后，爱动脑筋的小林想：如果把“‎6”‎换成字母“a”（且），能否求出的值？你的答案是（ ）‎ A. B. C. D.‎ ‎【答案】‎ 二、填空题（本大题共8个小题，每小题3分，共24分，请将答案填在答题卡上的答案栏内）‎ ‎9. jscm（2014湖南省永州市，9，3分）__________.‎ ‎【答案】2014‎ ‎10. jscm（2014湖南省永州市，10，3分）方程的解是__________.‎ ‎【答案】‎ ‎11.（2014湖南省永州市，11，3分）如图，已知AB∥CD，∠，则∠2=__________.‎ ‎【答案】‎ ‎12. （2014湖南省永州市，12，3分）不等式﹤-1的解集是__________.‎ ‎【答案】x﹤-4‎ ‎13. （2014湖南省永州市，13，3分）已知点A（1，），B（-2，）在反比例函数（k﹥0）的图象上，则______（填“﹥”、“﹤”或“=”）。‎ ‎【答案】﹤‎ ‎14. （2014湖南省永州市，14，3分）如图，有五张背面完全相同的纸质卡片，其正面分别标有数：6，，，-2，。将它们背面朝上洗匀后，从中随机抽取一张卡片，则其正面的数比3小的概率是__________.‎ ‎【答案】‎ ‎-2‎ ‎6‎ ‎15. （2014湖南省永州市，15，3分）如图，已知直线：与直线：交于点A，它们与y轴的交点分别为点B,C,点E,F分别为线段AB、AC的中点，则线段EF的长度为__________.‎ ‎【答案】‎ ‎16. （2014湖南省永州市，16，3分）小聪，小玲，小红三人参加“普法知识竞赛”‎ 其中前5题是选择题，每题10分，每题有A,B两个选项，且只有一个选项是正确的，三人的答案和得分如下表。试问：这五道题的正确答案（按第1～5题的顺序排列）是__________.‎ ‎【答案】B、A、B、B、A 三、解答题（本大题共有9个小题，共72分，解答题要求写出证明步骤或解答过程，并将答案填写在答题卡的答案栏内）‎ ‎17. jscm（2014湖南省永州市，17，6分）计算：‎ ‎【答案】解：‎ ‎ ‎ ‎ ‎ ‎18.jscm（2014湖南省永州市，18，6分）解方程组 ‎【答案】解：把①代入②，得：‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 把代入①，得：‎ ‎ 所以，原方程组的解为 ‎19. （2014湖南省永州市，19，6分）先化简，再求值：，其中。‎ ‎【答案】解：‎ ‎ ‎ ‎ ‎ ‎ 把代入上式，得：‎ ‎ ‎ ‎20. （2014湖南省永州市，20，8分）为了了解学生在一年中的课外阅读量，九（1）班对九年级800名学生采用随机抽样的方式进行了问卷调查，调查结果分为四种情况：A.10本以下；B.10‎ ‎～15本；C.16～20本；D.20本以上。根据调查结果统计整理并制作了如图所示的两幅不完整的统计图表：‎ ‎（1）在这次调查中一共抽查了_________名学生；‎ ‎（2）表中的值分别为：x=________,y=__________；‎ ‎（3）在扇形统计图中，C部分所对应的扇形的圆心角是________度；‎ ‎（4）根据抽样调查结果，请估计九年级学生中一年阅读课外书20本以上的学生人数。‎ 答案 选手 ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 得分 小聪 B A A B A ‎40‎ 小玲 B A B A A ‎40‎ 小红 A B B B A ‎30‎ ‎【答案】解：（1）200‎ ‎ （2）60，80‎ ‎（3）144‎ ‎（4）800×20℅=160名 ‎21.（2014湖南省永州市，21，8分）如图，D是△ABC的边AC上的一点，连结BD。已知∠ABD=∠C,AB=6,AD=4.求线段CD的长。‎ ‎【答案】解：∵∠ABD=∠C，∠A是公共角 ‎ ∴△ABD∽△ACB ‎ ∴‎ ‎ 即 ‎ ‎ ∴‎ ‎ ∴‎ ‎22. jscm（2014湖南省永州市，22，8分）某枇杷基地的枇杷成熟了，准备请专业摘果队帮忙摘果。现有甲、乙两支专业摘果队，若由甲队单独摘果，预计6天才能完成，为了减少枇杷因气候变化等原因带来的损失，现决定由甲、乙两队同时摘果，则2天可以完成，请问：‎ ‎（1）若单独由乙队摘果，需要几天才能完成?‎ ‎（2）若有三种摘果方案，方案1：单独请甲队；方案2：同时请甲、乙两队；方案3：单独请乙队。甲队每摘果一天，需支付给甲队1000元工资，乙队每摘果一天，需支付给乙队1600元工资。你认为用哪种方案完成所有摘果任务需支付给摘果队的总工资最低?最低工资是多少元？‎ ‎【答案】解：（1）设若单独由乙队摘果，需要x天才能完成。‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 经检验知，是原分式方程的解 ‎ ∴若单独由乙队摘果，需要3天才能完成.‎ ‎（2）方案1费用：1000×6=6000元 方案2费用：2×（1000+1600）=5200元 方案3费用：1600×3=4800元 因为 4800＜5200＜6000‎ 所以方案3完成所有摘果任务需支付给摘果队的总工资最低，最低工资为4800元。‎ ‎23. （2014湖南省永州市，23，10分）在同一平面内，△ABC和△ABD如图①放置，其中AB=BD。‎ 小明做了如下操作：‎ 将△ABC绕着边AC的中点旋转得到△CEA，将△ABD绕着边AD的中点旋转得到△DFA，如图②，请完成下列问题：‎ （1） 试猜想四边形ABDF是什么特殊四边形，并说明理由；‎ （2） 连接EF,CD，如图③，求证:四边形CDFE是平行四边形。‎ ‎【答案】（1）解：菱形，理由：‎ ‎ ∵△DFA是由△ABD绕边AD中点旋转得到的 ‎ ∴△ABD≌△DFA ‎ ∴AB=DF,BD=FA ‎ 又∵AB=BD ‎ ∴AB=BD=DF=FA ‎ ∴四边形ABDF是菱形 ‎(2)证明：由旋转性质可得: △ABC≌△CEA ‎ ∴AB=CE,BC=EA ‎ ∴四边形ABCE是平行四边形 ‎ ∴CE∥AB ‎ ∵四边形ABDF是菱形 ‎ ∴AB∥FD且，AB=FD ‎ ∴EC∥FD,且EC=FD ‎ ∴四边形CDFE是平行四边形。‎ ‎24. （2014湖南省永州市，24，10分）如图，点A是⊙O上一点，OA⊥AB，且OA=1，AB=，OB交⊙O于点D，作AC⊥OB，垂足为M，并交⊙O于点C，连结BC.‎ ‎（1）求证：BC是⊙O的切线；‎ ‎（2）过点B作BP⊥OB，交OA的延长线于点P，连结PD，求sin∠BPD的值。‎ ‎【答案】（1）证明：连结OC。‎ ‎ 在Rt△AOB中，‎ ‎ ∵‎ ‎ ∴‎ ‎ 由垂径定理可得：‎ ‎ ∴‎ ‎ 在Rt△AOM中，‎ ‎ ∴‎ ‎ 在Rt△ABM中,‎ ‎ 在△BOC中，∵OC=1,OB=2,‎ ‎ ∴‎ ‎ ∴OC⊥BC ‎ ∴BC是⊙O的切线.‎ ‎(2)解：∵∠AOB+∠ABO=‎ ‎ ∠POB+∠OPB=‎ ‎ ∴∠OBA=∠OPB ‎ 即：sin∠OPB=sin∠OBA=‎ ‎ ∴OP=2OB=4‎ ‎ ∴PB=‎ ‎ ∵OB=2,OD=1‎ ‎ ∴BD=1‎ ‎ 在Rt△PBD中，‎ ‎ ∴sin∠BPD=‎ ‎25. （2014湖南省永州市，25，10分）如图，抛物线与x轴交于两点，与y轴交于点,点是抛物线上一动点，位于对称轴的左侧，并且不在坐标轴上，过点M作x轴的平行线交y轴于点Q ，交抛物线于另一点E，直线BM交y轴于点F.‎ ‎（1）求抛物线的解析式，并写出其顶点坐标；‎ ‎（2）当时，求点M的坐标。‎ ‎【答案】解：(1)设抛物线解析式为 把点代入，得:‎ ‎ ‎ ‎ ‎ 把代入原式，得：‎ ‎ ‎ ‎ ‎ 即：抛物线的解析式为。‎ 对称轴为直线 ‎∵当时，‎ ‎∴顶点坐标为 ‎（2）∵点在抛物线上 ‎∴‎ 设直线BM解析式为 把点代入，得：‎ ‎，解得：‎ ‎∴‎ 则：‎ ‎∵，对称轴为直线 ‎∴‎ ‎∴‎ 则：‎