高考数学理试题分项版解析专题07 概率与统计

高考数学理试题分项版解析专题07 概率与统计

1.【2017 课标 1，理】如图，正方形 ABCD 内的图形来自中国古代的太极图.正方形内切圆 中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点 取自黑色部分的概率是 A． B． C． D． 2.【2017 课标 3，理 3】某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整 理了 2014 年 1 月至 2016 年 12 月期间月接待游客量（单位万人）的数据，绘制了下面的 折线图．中·华.资*源%库 ziyuanku.com 根据该折线图，下列结论错误的是 A．月接待游客量逐月增加 B．年接待游客量逐年增加 C．各年的月接待游客量高峰期大致在 7,8 月 D．各年 1 月至 6 月的月接待游客量相对 7 月至 12 月，波动性更小，变化比较平稳 3.【2017 浙江，8】已知随机变量 满足 P（ =1）=pi，P（ =0）=1—pi，i=1，2． 若 0 C． > ， < D． > ， > 1 4 π 8 1 2 π 4 iξ iξ iξ 1 2 1E( )ξ 2E( )ξ 1D( )ξ 2D( )ξ 1E( )ξ 2E( )ξ 1D( )ξ 2D( )ξ 1E( )ξ 2E( )ξ 1D( )ξ 2D( )ξ 1E( )ξ 2E( )ξ 1D( )ξ 2D( )ξ 4.【2017 山东，理 5】为了研究某班学生的脚长 （单位厘米）和身高 （单位厘米）的关 系，从该班随机抽取 10 名学生，根据测量数据的散点图可以看出 与 之间有线性相关关 系，设其回归直线方程为 ．已知 ， ， ．该班某学 生的脚长为 24，据此估计其身高为 （A） （B） （C） （D） 5.【2017 山东，理 8】从分别标有 ， ， ， 的 张卡片中不放回地随机抽取 2 次，每 次抽取 1 张．则抽到的 2 张卡片上的数奇偶性不同的概率是 （A） （B） （C） （D） 6.【2017 课标 II，理 13】一批产品的二等品率为 ，从这批产品中每次随机取一件，有 放回地抽取 次， 表示抽到的二等品件数，则 。 7.【2017 山东，理 18】（本小题满分 12 分）在心理学研究中，常采用对比试验的方法评价 不同心理暗示对人的影响，具体方法如下将参加试验的志愿者随机分成两组，一组接受甲种 心理暗示，另一组接受乙种心理暗示，通过对比这两组志愿者接受心理暗示后的结果来评价 两种心理暗示的作用，现有 6 名男志愿者 A1，A2，A3，A4，A5，A6 和 4 名女志愿者 B1，B2， B3，B4，从中随机抽取 5 人接受甲种心理暗示，另 5 人接受乙种心理暗示. （I）求接受甲种心理暗示的志愿者中包含 A1 但不包含 的频率。 8.【2017 课标 1，理 19】为了监控某种零件的一条生产线的生产过程，检验员每天从该生 产线上随机抽取 16 个零件，并测量其尺寸（单位 cm）．根据长期生产经验，可以认为这条 生产线正常状态下生产的零件的尺寸服从正态分布 ． （ 1 ） 假 设 生 产 状 态 正 常 ， 记 X 表 示 一 天 内 抽 取 的 16 个 零 件 中 其 尺 寸 在 之外的零件数，求 及 的数学期望； （2）一天内抽检零件中，如果出现了尺寸在 之外的零件，就认为这 条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查． （ⅰ）试说明上述监控生产过程方法的合理性； （ⅱ）下面是检验员在一天内抽取的 16 个零件的尺寸 9.95 10.1 2 9.96 9.96 10.0 1 9.92 9.98 10.0 4 10.2 9.91 10.1 10.0 9.22 10.0 10.0 9.95 x y y x ˆˆ ˆy bx a= + 10 1 225i i x = =∑ 10 1 1600i i y = =∑ ˆ 4b = 160 163 166 170 1 2 ⋅⋅⋅ 9 9 5 18 4 9 5 9 7 9 0.02 100 Χ DΧ = 1B 2( , )N µ σ ( 3 , 3 )µ σ µ σ− + ( 1)P X ≥ X ( 3 , 3 )µ σ µ σ− + 6 3 2 4 5 经计算得 ， ， 其中 为抽取的第 个零件的尺寸， ． 用样本平均数 作为 的估计值 ，用样本标准差 作为 的估计值 ，利用估计值 判断是否需对当天的生产过程进行检查？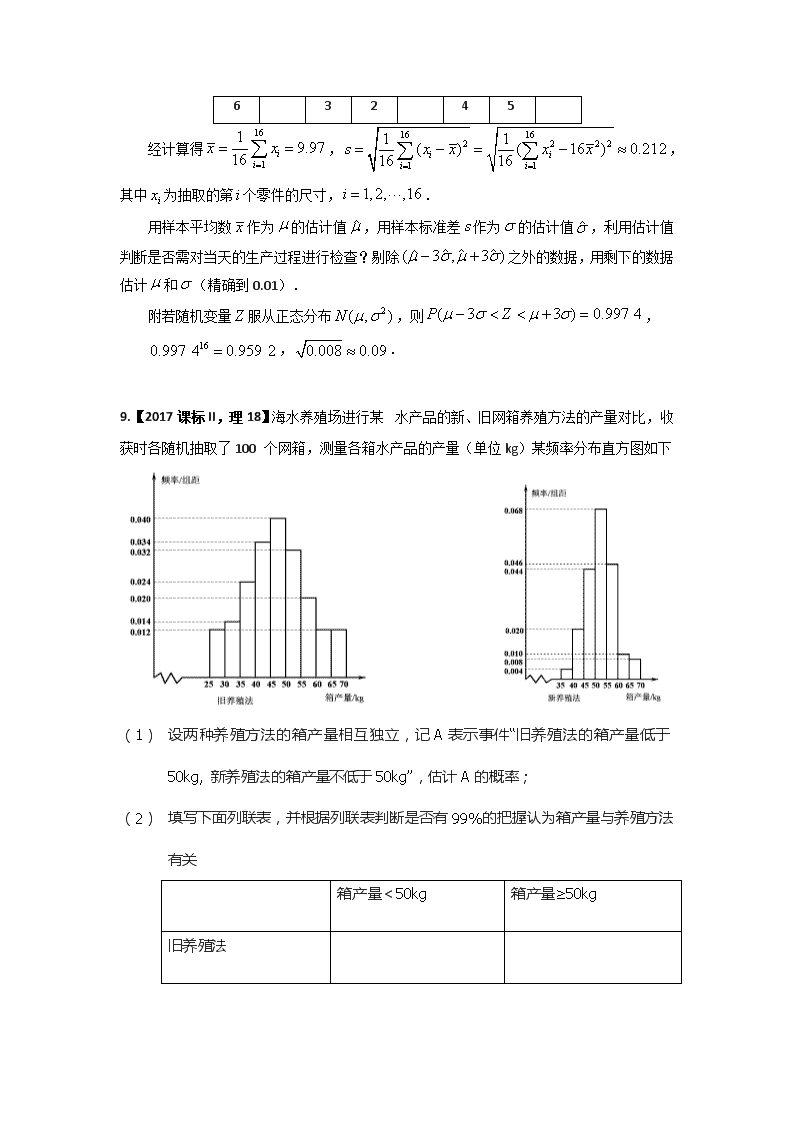剔除 之外的数据，用剩下的数据 估计 和 （精确到 0.01）． 附若随机变量 服从正态分布 ，则 ， ， ． 9.【2017 课标 II，理 18】海水养殖场进行某 Ziyuanku.com水产品的新、旧网箱养殖方法的产量对比，收 获时各随机抽取了 100 个网箱，测量各箱水产品的产量（单位 kg）某频率分布直方图如下 （1） 设两种养殖方法的箱产量相互独立，记 A 表示事件“旧养殖法的箱产量低于 50kg, 新养殖法的箱产量不低于 50kg”，估计 A 的概率； （2） 填写下面列联表，并根据列联表判断是否有 99%的把握认为箱产量与养殖方法 有关 箱产量＜50kg 箱产量≥50kg 旧养殖法 16 1 1 9.9716 i i x x = = =∑ 16 16 2 2 2 2 1 1 1 1( ) ( 16 ) 0.21216 16i i i i s x x x x = = = − = − ≈∑ ∑ ix i 1,2, ,16i = ⋅⋅⋅ x µ ˆµ s σ ˆσ ˆ ˆ ˆ ˆ( 3 , 3 )µ σ µ σ− + µ σ Z 2( , )N µ σ ( 3 3 ) 0.997 4P Zµ σ µ σ− < < + = 160.997 4 0.959 2= 0.008 0.09≈ 新养殖法 （3） 根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到 0.01） 附 。 （2）根据箱产量的频率分布直方图得列联表 箱产量 箱产量 旧养殖法 62 38 新养殖法 34 66 由于 ，故有 的把握认为箱产量与养殖方法有关。 【考点】 独立事件概率公式；独立性检验原理；频率分布直方图估计中位数。 【名师点睛】利用独立性检验，能够帮助我们对日常生活中的实际问题作出合理 的推断和预测。独立性检验就是考察两个分类变量是否有关系，并能较为准确地 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d −= + + + + 50kg< 50kg≥ ( )2 2 200 62 66 34 38 15.705100 100 96 104K × × − ×= ≈× × × 15.705 6.635> 99% 给出这种判断的可信度，随机变量的观测值 值越大，说明“两个变量有关系” 的可能性越大。 利用频率分布直方图求众数、中位数和平均数时，应注 Ziyuanku.com 中/华-资*源%库意三点①最高的小长 方形底边中点的横坐标即是众数；②中位数左边和右边的小长方形的面积和是相 等的；③平均数是频率分布直方图的“重心”，等于频率分布直方图中每个小长方 形的面积乘以小长方形底边中点的横坐标之和。 10.【2017 北京，理 17】为了研究一种新药的疗效，选100 名患者随机分成两组，每组各 50 名，一组服药，另一组不服药.一段时间后，记录了两组患者的生理指标 x 和 y 的数据，并 制成下图，其中“*”表示服药者，“+”表示未服药者. （Ⅰ）从服药的 50 名患者中随机选出一人，求此人指标 y 的值小于 60 的概率； （Ⅱ）从图中 A，B，C，D 四人中随机选出两人，记 为选出的两人中指标 x 的值大于 1.7 的人数，求 的分布列和数学期望 E（ ）； （Ⅲ）试判断这 100 名患者中服药者指标 y 数据的方差与未服药者指标 y 数据的方差的大小. （只需写出结论） 【答案】（Ⅰ）0.3；（Ⅱ）详见解析；（Ⅲ）在这 100 名患者中，服药者指标 数据的方差 大于未服药者指标 数据的方差. 【解析】 2K ξ ξ ξ y y （Ⅱ）由图知，A,B,C,D 四人中，指标 的值大于 1.7 的有 2 人 A 和 C. 所以 的所有可能取值为 0,1,2. . 所以 的分布列为 0 1 2 故 的期望 . （Ⅲ）在这 100 名患者中，服药者指标 数据的方差大于未服药者指标 数据的方差.[ 【考点】1.古典概型；2.超几何分布；3.方差的定义. 【名师点睛】求分布列的三种方法 1．由统计数据得到离散型随机变量的分布列； 2．由古典概型求出离散型随机变量的分布列； 3．由互斥事件的概率、相互独立事件同时发生的概率及 n 次独立重复试验有 k 次发生的概 率求离散型随机变量的分布列． 11.【2017 天津，理 16】从甲地到乙地要经过 3 个十字路口，设各路口信号灯工作相互独立， 且在各路口遇到红灯的概率分别为 . （Ⅰ）设 表示一辆车从甲地到乙地遇到红灯的个数，求随机变量 的分布列和数学期望； （Ⅱ）若有 2 辆车独立地从甲地到乙地，求这 2 辆车共遇到 1 个红灯的概率. x ξ 2 1 1 2 2 2 2 2 2 2 2 4 4 4 C C C C1 2 1( 0) , ( 1) , ( 2)C 6 C 3 C 6P P Pξ ξ ξ= = = = = = = = = ξ ξ P 1 6 2 3 1 6 ξ 1 2 1( ) 0 1 2 16 3 6E ξ = × + × + × = y y 1 1 1, ,2 3 4 X X 【答案】 (1) (2) 所以，随机变量 的分布列为 0 1 2 3 随机变量 的数学期望 . 【考点】离散型随机变量概率分布列及数学期望中/华-资*源%库 【名师点睛】求离散型随机变量概率分 WWW.ziyuanku.com布列问题首先要清楚离散型随机变量的可取值有 那些？当随机变量取这些值时所对应的事件的概率有是多少，计算出概率值后，列出离散型 随机变量概率分布列，最后按照数学期望公式计算出数学期望.；列出离散型随机变量概率 分布列及计算数学期望是理科高考数学必考问题. 12.【2017 课标 3，理 18】某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶 4 元，售价每瓶 6 元，未售出的酸奶降价处理，以每瓶 2 元的价格当天全部处理完.根据往年 销售经验，每天需求量与当天最高气温（单位℃）有关.如果最高气温不低于 25，需求量为 500 13 12 11 48 X X P 1 4 11 24 1 4 1 24 X 1 11 1 1 13( ) 0 1 2 34 24 4 24 12E X = × + × + × + × = 瓶；如果最高气温位于区间[20，25），需求量为 300 瓶；如果最高气温低于 20，需求量为 200 瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数 分布表 最高气温 [10，15） [15，20） [20，25） [25，30） [30，35） [35，40） 天 数 2 1 6 3 6 2 5 7 4 以最高气温位于各区间的频率代替最高气温位于该区间的概率. （1）求六月份这种酸奶一天的需求量 X（单位瓶）的分布列； （2）设六月份一天销售这种酸奶的利润为 Y（单位元）.当六月份这种酸奶一天的进货 量 n（单位瓶）为多少时，Y 的数学期望达到最大值？ 【答案】(1)分布列略； (2) n=300 时，Y 的数学期望达到最大值，最大值为 520 元. 【解析】 试题分析(1) 所有的可能取值为 200,300,500，利用题意求得概率即可得到随机变量的分 布列； (2)由题中所给条件分类讨论可得 n=300 时，Y 的数学期望达到最大值 520 元. 试题解析（1）由题意知， 所有的可能取值为 200,300,500，由表格数据知 ， ， . 因此 的分布列为 0.2 0.4 0.4 X X ( ) 2 16200 0.290P X += = = ( ) 36300 0.490P X = = = ( ) 25 7 4500 0.490P X + += = = X X 200 300 500 P 【考点】 离散型随机变量的分布列；数学期望； 【名师点睛】离散型随机变量的分布列指出了随机变量 X 的取值范围以及取各 值的概率；要理解两种特殊的概率分布——两点分布与超几何分布；并善于灵活 运用两性质一是 pi≥0(i＝1,2，…)；二是 p1＋p2＋…＋pn＝1 检验分布列的正误. WWW.ziyuanku.com 13. 【2017 江苏，23】 已知一个口袋有 个白球, 个黑球( ),这些球除颜 色 外 全 部 相 同 . 现 将 口 袋 中 的 球 随 机 的 逐 个 取 出 ， 并 放 入 如 图 所 示 的 编 号 为 的 抽 屉 内 ， 其 中 第 次 取 出 的 球 放 入 编 号 为 的 抽 屉 . 1 2 3 （1）试求编号为 2 的抽屉内放的是黑球的概率 ; （2）随机变量 表示最后一个取出的黑球所在抽屉编号的倒数, 是 的数学期望, 证明 【答案】（1） （2）见解析 m n , *, 2m n n∈N ≥ 1, 2, 3, , m n+ k k ( 1, 2, 3, , )k m n= +  m n+ p X ( )E X X ( ) ( )( 1) nE X m n n < + − n m n+ 【解析】解(1) 编号为 2 的抽屉内放的是黑球的概率 为 . (2) 随机变量 X 的概率分布为 X … … P … … 随机变量 X 的期望为 【考点】古典概型概率、随机变量及其分布、数学期望 【名师点睛】求解离散型随机变量的数学期望的一般步骤为 第一步是“判断取值”，即判断随机变量的所有可能取值，以及取每个值所表示的意义； 第二步是“探求概率”，即利用排列组合、枚举法、概率公式(常见的有古典概型公式、几何 概型公式、互斥事件的概率和公式、独立事件的概率积公式，以及对立事件的概率公式等)， 求出随机变量取每个值时的概率； 第三步是“写分布列”，即按规范形式写出分布列，并注意用分布列的性质检验所求的分布 p 1 1C C n m n n m n np m n − + − + = = + 1 n 1 1n + 1 2n + 1 k 1 m n+ 1 1C C n n n m n − − + 1C C n n n m n − + 1 1C C n n n m n − + + 1 1C C n k n m n − − + 1 1C C n n m n m n − + − + 列或某事件的概率是否正确； 第四步是“求期望值”，一般利用离散型随机变量的数学期望的定义求期望的值，对于有些 实际问题中的随机变量，如果能够断定它服从某常见的典型分布(如二项分布 )， 则此随机变量的期望可直接利用这种典型分布的期望公式( )求得.因此，应熟记 常见的典型分布的期望公式，可加快解题速度. 24.【2017 江苏，3】 某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为 200,400,300,100 件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取 60 件进行检验,则应从丙种型号的产品中抽取 ▲ 件. 【答案】18 【解析】所求人数为 ，故答案为 18． 【考点】分层抽样 【名师点睛】在分层抽样的过程中，为了保证每个个体被抽到的可能性是相同的，这就 要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之 比，即 ni∶Ni＝n∶N. 25.【2017 江苏，7】 记函数 的定义域为 .在区间 上随机取一个数 ,则 的概率是 ▲ . 【答案】 【考点】几何概型概率 【名师点睛】(1)当试验的结果构成的区域为长度、面积、体积等时，应考虑使 用几何概型求解． ( , )X B n p ( )E X np= 30060 1810000 × = 2( ) 6f x x x= + − D [ 4,5]− x x D∈ 5 9 (2)利用几何概型求概率时，关键是试验的全部结果构成的区域和事件发生的区 域的寻找，有时需要设出变量，在坐标系中表示所需要的区域. （3）几何概型有两个特点一是无限性，二是等可能性．基本事件可以抽象为点，尽管这些 点是无限的，但它们所占据的区域都是有限的，因此可用“比例解法”求解几何概型的概 率．