- 2021-05-10 发布 |
- 37.5 KB |
- 21页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学压轴题整理
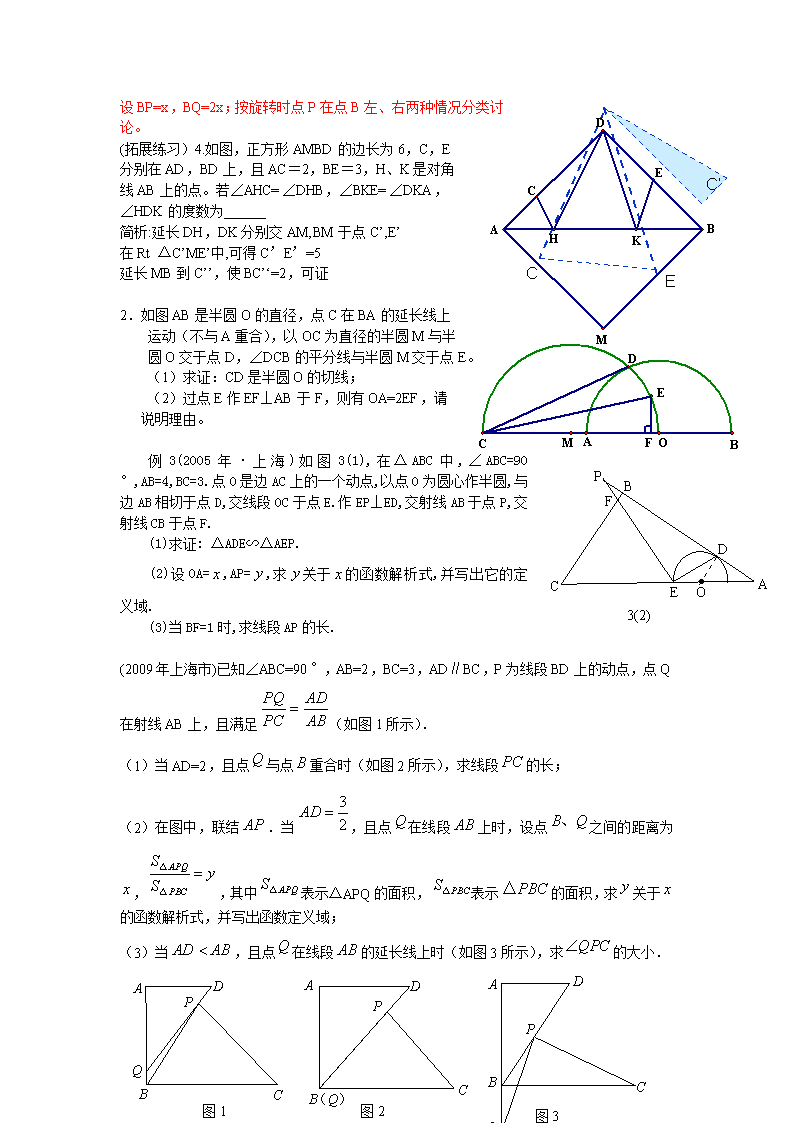
26、(2009年济宁市)在平面直角坐标中,边长为2的正方形的两顶点、分别在轴、轴的正半轴上,点在原点.现将正方形绕点顺时针旋转,当点第一次落在直线上时停止旋转,旋转过程中,边交直线于点,边交轴于点(如图). O A B C M N (1)求边在旋转过程中所扫过的面积; (2)旋转过程中,当和平行时,求正方形旋转的度数; (3)设的周长为,在旋转正方形的过程中,值是否有变化?请证明你的结论. 提示:延长BA交y轴于点E。第(3)问, 证明△OAE≌△OCN , △OMN≌△OME, 得MN=AM+CN. 27、(2009年宁波市) (Q) B A O x P (图2) y Q C B A O x P (图1) y C B A O y x (备用图) (第27题) 如图1,在平面直角坐标系中,O为坐标原点,点A的坐标为,直线BC经过点,,将四边形OABC绕点O按顺时针方向旋转度得到四边形,此时直线、直线分别与直线BC相交于点P、Q. (1)四边形OABC的形状是 , 当时,的值是 ; (2)①如图1,当四边形的顶点落在轴正半轴时,求的值; ②如图,当四边形的顶点落在直线上时,求的面积. (3)在四边形OABC旋转过程中,当时,是否存在这样的点P和点Q,使?若存在,请直接写出点P的坐标;若不存在,请说明理由. 提示:第(3)问,过点Q作QH⊥OA'于H,连接OQ,则QH=OC'=OC,易证PQ=OP, 设BP=x,BQ=2x;按旋转时点P在点B左、右两种情况分类讨论。 C’ E’ (拓展练习)4.如图,正方形AMBD的边长为6,C,E C’’ 分别在AD,BD上,且AC=2,BE=3,H、K是对角 线AB上的点。若∠AHC=∠DHB,∠BKE=∠DKA, ∠HDK的度数为______ 简析:延长DH,DK分别交AM,BM于点C’,E’ 在Rt △C’ME’中,可得C’E’=5 延长MB到C’’,使BC’‘=2,可证 2.如图AB是半圆O的直径,点C在BA的延长线上 运动(不与A重合),以OC为直径的半圆M与半 圆O交于点D,∠DCB的平分线与半圆M交于点E。 (1)求证:CD是半圆O的切线; (2)过点E作EF⊥AB于F,则有OA=2EF,请 说明理由。 ● P D E A C B 3(2) O F 例3(2005年·上海)如图3(1),在△ABC中,∠ABC=90°,AB=4,BC=3. 点O是边AC上的一个动点,以点O为圆心作半圆,与边AB相切于点D,交线段OC于点E.作EP⊥ED,交射线AB于点P,交射线CB于点F. (1)求证: △ADE∽△AEP. (2)设OA=,AP=,求关于的函数解析式,并写出它的定义域. (3)当BF=1时,求线段AP的长. (2009年上海市)已知∠ABC=90°,AB=2,BC=3,AD∥BC,P为线段BD上的动点,点Q在射线AB上,且满足(如图1所示). (1)当AD=2,且点与点重合时(如图2所示),求线段的长; (2)在图中,联结.当,且点在线段上时,设点之间的距离为,,其中表示△APQ的面积,表示的面积,求关于的函数解析式,并写出函数定义域; (3)当,且点在线段的延长线上时(如图3所示),求的大小. A D P C B Q 图1 D A P C B (Q) ) 图2 图3 C A D P B Q (2009年义乌)如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原。 (1)当时,折痕EF的长为;当点E与点A重合时,折痕EF的长为; (2)请写出使四边形EPFD为菱形的的取值范围,并求出当时菱形的边长; (3)令,当点E在AD、点F在BC上时,写出与的函数关系式。当取最大值时,判断与是否相似?若相似,求出的值;若不相似,请说明理由。 (2009年济宁市)如图,中,,,.半径为1的圆的圆心以1个单位/的速度由点沿方向在上移动,设移动时间为(单位:). (1)当为何值时,⊙与相切; (2)作交于点,如果⊙和线段交于点,证明:当时,四边形为平行四边形. (2009年广西钦州)如图,已知抛物线y=x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1. (1)填空:点C的坐标是_▲_,b=_▲_,c=_▲_; (2)求线段QH的长(用含t的式子表示); (3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由. (09湖北宜昌)(09湖北宜昌)已知:如图1,把矩形纸片ABCD折叠,使得顶点A与边DC上的动点P重合(P不与点D,C重合), MN为折痕,点M,N分别在边BC, AD上,连接AP,MP,AM, AP与MN相交于点F.⊙O过点M,C,P. (1)请你在图1中作出⊙O(不写作法,保留作图痕迹); (2)与 是否相等?请你说明理由; (3)随着点P的运动,若⊙O与AM相切于点M时,⊙O又与AD相切于点H. 设AB为4,请你通过计算,画出这时的图形.(图2,3供参考) 图1 图2 图3 (2009年茂名市)如图,在中, 点是边上的动点(点与点不重合),过动点作交于点 (1)若与相似,则是多少度? (2分) (2)试问:当等于多少时,的面积最大?最大面积是多少? (4分) (3)若以线段为直径的圆和以线段为直径的圆相外切,求线段的长.(4分) (2009年山东青岛市)如图,在梯形ABCD中,,,,,点由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交于Q,连接PE.若设运动时间为(s)().解答下列问题: (1)当为何值时,? (2)设的面积为(cm2),求与之间的函数关系式; (3)是否存在某一时刻,使?若存在,求出此时的值;若不存在,说明理由. (4)连接,在上述运动过程中,五边形的面积是否发生变化?说明理由. 10、(2008 湖北 恩施) 如图11,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n. (1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明. (2)求m与n的函数关系式,直接写出自变量n的取值范围. (3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图12).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD+CE=DE. (4)在旋转过程中,(3)中的等量关系BD+CE=DE是否始终成立,若成立,请证明,若不成立,请说明理由. G y x O F E D C B A G F E D C B A A B C D E R P H Q (第1题图) 11、 (08浙江温州)如图,在中,,,,分别是边的中点,点从点出发沿方向运动,过点作于,过点作交于,当点与点重合时,点停止运动.设,. (1)求点到的距离的长; (2)求关于的函数关系式(不要求写出自变量的取值范围); (3)是否存在点,使为等腰三角形?若存在,请求出所有满足要求的的值;若不存在,请说明理由. 18、在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x. (1)用含x的代数式表示△MNP的面积S; (2)当x为何值时,⊙O与直线BC相切? (3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少? A B C M N P 图 3 O A B C M N D 图 2 O A B C M N P 图 1 O 3.如图,在平面直角坐标系xOy中,已知点A(4,0),点B(0,3),点P从点B出发沿BA方向向点A 匀速运动,速度为每秒1个单位长度,点Q从点A出发沿AO方向向点O匀速运动,速度为每秒2个单位长度,连结PQ.若设运动的时间为t秒(0<t<2). (1)求直线AB的解析式; (2)设△AQP的面积为,求与之间的函数关系式; (3)是否存在某一时刻,使线段PQ恰好把△AOB的周长和面积同时平分?若存在,请求出此时的值;若不存在,请说明理由; (4)连结PO,并把△PQO沿QO翻折,得到四边形,那么是否存在某一时刻,使四边形为菱形?若存在,请求出此时点Q的坐标和菱形的边长;若不存在,请说明理由. 4.在平面直角坐标系中,抛物线经过直线与坐标轴的两个交点,它与x轴的另一个交点为.点是抛物线对称轴与轴的交点,点为线段上的动点. (1)求抛物线的解析式及点的坐标; (2)如图①,若过动点的直线交抛物线对称轴于点.试问抛物线上是否存在点,使得以点为顶点组成的四边形是平行四边形,若存在,求出点的坐标;若不存在,说明理由; (3)如图②,若过动点的直线交直线于,连接.当的面积最大时,求点的坐标? 图① 图② 21.(2006云南课改中考,25)如图1-3-8,在直角坐标系中,O为坐标原点,OABC的边OA在x轴上,∠B=60°,OA=6,OC=4,D是BC的中点,延长AD交OC的延长线于点E. 图1-3-8 (1)画出△ECD关于边CD所在直线为对称轴的对称图形△E1CD,并求出点E1的坐标; (2)求经过C、E1、B三点的抛物线的函数表达式; (3)请探求经过C、E1、B三点的抛物线上是否存在点P,使以点P、B、C为顶点的三角形与△ECD相似.若存在这样的点P,请求出点P的坐标;若不存在这样的点P,请说明理由. 9.(2010年江苏省泰州市济川实验初中中考模拟题) 如图1,把一个边长为2的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边). (1)求抛物线c1的解析式及点M、N的坐标; (2)如图2,另一个边长为2的正方形的中心G在点M上,、在x轴的负半轴上(在的左边),点在第三象限,当点G沿着抛物线c1从点M移到点N,正方形随之移动,移动中始终与x轴平行. ①直接写出点、移动路线形成的抛物线、的函数关系式; ②如图3,当正方形第一次移动到与正方形ABCD有一边在同一直线上时, 求点G的坐标. 10.(2010广东省中考拟)如图10,在平面直角坐标系中,二次函数的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=. (1)求这个二次函数的表达式. (2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由. (3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度. (4)如图11,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积. _ y _ x _ O _ E _ D _ C _ B _ A 图10 _ G _ A _ B _ C _ D _ O _ x _ y 图11 A y x B E F O1 Q O O2 C 4.(2004湖北襄樊)如图,在平面直角坐标系内,Rt△ABC的直角顶点C(0,)在轴的正半轴上,A、B是轴上是两点,且OA∶OB=3∶1,以OA、OB为直径的圆分别交AC于点E,交BC于点F.直线EF交OC于点Q. (1)求过A、B、C三点的抛物线的解析式; (2)请猜想:直线EF与两圆有怎样的位置关系?并证明你的猜想. (3)在△AOC中,设点M是AC边上的一个动点,过M作MN∥AB交OC于点N.试问:在轴上是否存在点P,使得△PMN是一个以MN为一直角边的等腰直角三角形?若存在,求出P点坐标;若不存在,请说明理由. (第9题图) A y x O N M G F E D C B 9. 如图,⊙M与x轴交于A、B两点,其坐标分别为、,直径CD⊥x轴于N,直线CE切⊙M于点C,直线FG切⊙M于点F,交CE于G,已知点G的横坐标为3. (1) 若抛物线经过A、B、D三点,求m的值及点D的坐标. (2) 求直线DF的解析式. (3) 是否存在过点G的直线,使它与(1)中抛物线的两个交点的横坐标之和等于4?若存在,请求出满足条件的直线的解析式;若不存在,请说明理由. 12.(2005北京)已知:在平面直角坐标系xOy中,一次函数的图象与x轴交于点A,抛物线经过O、A两点。 (1)试用含a的代数式表示b; (2)设抛物线的顶点为D,以D为圆心,DA为半径的圆被x轴分为劣弧和优弧两部分。若将劣弧沿x轴翻折,翻折后的劣弧落在⊙D内,它所在的圆恰与OD相切,求⊙D半径的长及抛物线的解析式; (3)设点B是满足(2)中条件的优弧上的一个动点,抛物线在x轴上方的部分上是否存在这样的点P,使得?若存在,求出点P的坐标;若不存在,请说明理由。 A · B C D E F G M x y O 16.(2005湖北荆门)已知:如图,抛物线与x轴交于A、B两点,与y轴交于C点,∠ACB=90°, (1)求m的值及抛物线顶点坐标; (2)过A、B、C的三点的⊙M交y轴于另一点D,连结DM并延长交⊙M于点E,过E点的⊙M的切线分别交x轴、y轴于点F、G,求直线FG的解析式; (3)在(2)条件下,设P为上的动点(P不与C、D重合),连结PA交y轴于点H,问是否存在一个常数k,始终满足AH·AP=k,如果存在,请写出求解过程;如果不存在,请说明理由. A B C O 图8 H 例4(2004年·上海)如图,在△ABC中,∠BAC=90°,AB=AC=,⊙A的半径为1.若点O在BC边上运动(与点B、C不重合),设BO=,△AOC的面积为. (1)求关于的函数解析式,并写出函数的定义域. (2)以点O为圆心,BO长为半径作圆O,求当⊙O与⊙A相切时, △AOC的面积. 1.(09年徐汇区)如图,中,,,点在边上,且,以点为顶点作,分别交边于点,交射线于点. (1)当时,求的长; (2)当以点为圆心长为半径的⊙和以点为圆心长为半径的⊙相切时, 求的长; (3)当以边为直径的⊙与线段相切时,求的长. 在矩形ABCD中,AB=3,点O在对角线AC上,直线l过点O,且与AC垂直交AD于点E.(1)若直线l过点B,把△ABE沿直线l翻折,点A与矩形ABCD的对称中心A'重合,求BC的长; A B C D E O l A′ (2)若直线l与AB相交于点F,且AO=AC,设AD的长为,五边形BCDEF的面积为S.①求S关于的函数关系式,并指出的取值范围; ②探索:是否存在这样的,以A为圆心,以长为半径的圆与直线l相切,若存在,请求出的值;若不存在,请说明理由. [类题] 改编自09奉贤3月考25题,将条件(2)“当点M、N分别在边BA、CA上时”,去掉,同时加到第(3)题中. A B F D E M N C 已知:在△ABC中,AB=AC,∠B=30º,BC=6,点D在边BC上,点E在线段DC上,DE=3,△DEF是等边三角形,边DF、EF与边BA、CA分别相交于点M、N. (1)求证:△BDM∽△CEN; (2)设BD=,△ABC与△DEF重叠部分的面积为,求关于的函数解析式,并写出定义域. (3)当点M、N分别在边BA、CA上时,是否存在点D,使以M为圆心, BM为半径的圆与直线EF相切, 如果存在,请求出x的值;如不存在,请说明理由. 例1:已知⊙O的弦AB的长等于⊙O的半径,点C在⊙O上变化(不与A、B)重合,求∠ACB的大小 . 变式1:已知△ABC是半径为2的圆内接三角形,若,求∠C的大小. 变式2: 如图,半经为1的半圆O上有两个动点A、B,若AB=1, 判断∠AOB的大小是否会随点A、B的变化而变化,若变化,求出变化范围,若不变化,求出它的值。 四边形ABCD的面积的最大值。 例2:(2004年广州市中考题第11题)如图,⊙O1和⊙O2内切于A,⊙ O1的半径为3,⊙O2的半径为2,点P为⊙O1上的任一点(与点A不重合),直线PA交⊙O2于点C,PB切⊙O2于点B,则的值为 (A) (B) (C) (D) 例7:如图,在等腰直角三角形ABC中,斜边BC=4,OABC于O,点E和点F分别在边AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与B、A重合。 判断四边形AEOF的面积是否随点E、F的变化而变化,若变化,求其变化范围,若不变化,求它的值. AEF的面积是否随着点E、F的变化而变化,若变化,求其变化范围,若不变化,求它的值。 (即例3的第2、第3问) 分析:(2)本题的方法很多,其一,可以建立四边形AEOF与AE长的函数关系式,如设AE=x,则AF=, 而三角形AOB的面积与三角形AOE的面积之比=,而三角形AOB的面积=,则三角形AOE的面积=,同理三角形AOF的面积=,因此四边形AEOF的面积=;即AEOF的面积不会随点E、F的变化而变化,是一个定值,且为2. 当然,本题也可以这样思考,由于三角形AOE与三角形COF全等,则四边形AEOF的面积与三角形AOC的面积相等,而AOC的面积为2,因此AEOF的面积不会随点E、F的变化而变化,是一个定值,且为2. 本题通过建立函数关系或有关图形之间的关系,然后通过简单的计算得出结论的方法应用比较广泛. 第(3)问,也可以通过建立函数关系求得, AEF的面积=,又的变化范围为,由二次函数知识得AEF的面积的范围为: AEF的面积. 本题也可以根据三角形AEF与三角形OEF的面积关系确定AEF的面积范围: 不难证明AEF的面积≤OEF的面积,它们公用边EF,取EF的中点H,显然由于OEF为等腰直角三角形,则OH⊥EF,作AG⊥EF,显然AG≤AH=AG(=),所以AEF的面积≤OEF的面积,而它们的和为2,因此AEF的面积. 本题包容的内涵十分丰富,还可以提出很多问题研究: 比如,比较线段EF与AO长度大小等(可以通过A、E、O、F四点在以EF为直径的圆上得出很多结论) 练习1:2003年广州市中考压轴题(全卷得分最低的一道) 已知ABC为直角三角形,AC=5,BC=12,∠ACB为直角,P是AB边上的动点(与点A、B不重合),Q是BC边上动点(与点B、C不重合) (1) 如图,当PQ∥AC,且Q为BC的中点,求线段CP的长。 当PQ与AC不平行时,CPQ可能为直角三角形吗?若有可能,求出线段CQ的长的取值范围;若不可能,请说明理由。 第1问很易得出P为AB中点,则CP= 第2问:如果CPQ为直角三角形,由于PQ与AC不平行,则∠Q不可能为直角 又点P不与A重合,则∠PCQ也不可能为直角,只能是∠CPQ为直角,即以CQ为直径的圆与AB有交点,设CQ=2x,CQ的中点D到AB的距离DM不大于CD, ,即,所以,由,即,而,故,亦即时,CPQ可能为直角三角形。 当然还有其它方法。同学们可以继续研究。 练习3、在平面直角坐标系中,已知二次函数的图象与轴交于两点(点在点的左边),与轴交于点,其顶点的横坐标为1,且过点和. (1)求此二次函数的表达式;(由一般式得抛物线的解析式为) (2)若直线与线段交于点(不与点重合),则是否存在这样的直线,使得以为顶点的三角形与相似?若存在,求出该直线的函数表达式及点的坐标;若不存在,请说明理由; C B A 练习4图 P y y C x B A 练习3图 (3)若点是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角与的大小(不必证明),并写出此时点的横坐标的取值范围. O 练习4 (2008广东湛江市) 如图所示,已知抛物线与轴交于A、B两点,与轴交于点C. (1)求A、B、C三点的坐标. (2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积. (3)在轴上方的抛物线上是否存在一点M,过M作MG轴于点G,使以A、M、G三点为顶点的三角形与PCA相似.若存在,请求出M点的坐标;否则,请说明理由. 例2. 如图2,直角梯形ABCD中,AD∥BC,∠B=90°,AD+BC<DC,若腰DC上有动点P,使AP⊥BP,则这样的点有多少个? 分析:由条件AP⊥BP,想到以AB为直径作圆,若CD与圆相交,根据直径所对的圆周角是90°,两个交点即为点P;若CD与圆相切,切点即是点P;若CD与圆相离,则DC上不存在动点P,使AP⊥BP。 解:如图3,以AB为直径做⊙O,设⊙O与CD切于点E 因为∠B=∠A=90° 所以AD、BC为⊙O的切线 即AD=DE,BC=CE 所以AD+BC=CD 而条件中AD+BC<DC,我们把CD向左平移,如图4,CD的长度不变,AD与BC的长度缩短,此时AD+BC<DC,点O到CD的距离OE�小于⊙O的半径OE,CD与⊙O 相交,和是直径AB所对的圆周角,都为90°,所以交点即为所求。因此,腰DC上使AP⊥BP的动点P有2个。 例1 (2006年福建晋州)如图,在平行四边形ABCD中,AD=4cm,∠A=60°,BD⊥AD.一动点P从A出发,以每秒1cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD. 1.当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积; 2.当点P运动2秒时,另一动点Q也从A出发沿A→B的路线运动,且在AB上以每秒1cm的速度匀速运动,(当P、Q中的某一点到达终点,则两点都停止运动.)过Q作直线QN,使QN∥PM,设点Q运动的时间为t秒(0≤t≤8),直线PM与QN截平行四边形ABCD所得图形的面积为S(cm2). (1)求S关于t的函数关系式; (2)求S的最大值. 例2.(2006年锦州市)如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方). 1.求A、B两点的坐标; 2.设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式; 3.在题(2)的条件下,t为何值时,S的面积最大?最大面积是多少? 3(09深圳)如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P. (1)连结PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由; (2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形? 9(09兰州)如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4), 点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动, 同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动, 设运动的时间为t秒. (1)当P点在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度; (2)求正方形边长及顶点C的坐标; (3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标; (4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由. 12(09太原)问题解决 图(2) N A B C D E F M 如图(1),将正方形纸片折叠,使点落在边上一点(不与点,重合),压平后得到折痕.当时,求的值. 方法指导: 为了求得的值,可先求、的长,不妨设:=2 类比归纳 在图(1)中,若则的值等于 ;若则的值等于 ;若(为整数),则的值等于 .(用含的式子表示) 联系拓广 如图(2),将矩形纸片折叠,使点落在边上一点(不与点重合),压平后得到折痕设则的值等于 .(用含的式子表示) 【出自华夏】 1、已知正方形ABCD,E、F分别为BC、AB边上的点,且BE=BF,BH⊥CF于H,连结DH. 求证:DH⊥EH. 2、已知AD⊥BC于D,AE:ED=CD:BD,DF⊥BE于F,求证:AF⊥CF. 3、已知正方形ABCD,E为对角线AC上一点,AE=3CE,F为AB边中点,求证:DE⊥EF. 4、已知B是AC的中点,D、E在AC的同侧,且∠ADB=∠EBC,∠A=∠C, 求证:∠BDE=∠BDA. 5、等腰△ADE中,AD=AE (1)若∠DAE=90°,∠BAC=135°,求证:AD2=BD×CE; (2)若∠BAC=100°,则当∠DAE为多少度时,AD2=BD×CE 6、已知四边形ABCD,AD⊥AB,BC⊥AB,BC=2AD, DE⊥CD, (1)求证:DE2=AE×CE; (2)求证:; (3)若△CDE与四边形ABCD的面积字之比为2:5,求的值。 7、已知AB∥CD,DB=DC,点E是BC的中点, 求证: 8、设△ABC中,D在BC上,且, 求证: 9、正△ABC中,D在BC上,BD:DC=1:2, 求证:∠DBH=∠BAD. 11、如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF. 解答下列问题: (1)如果AB=AC,∠BAC=90º. ①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 . 图甲 图乙 图丙 ②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么? (2)如果AB≠AC,∠BAC≠90º,点D在线段BC上运动. 试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法) (3)若AC=,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值. 12、已知:如图①所示,在和中,,,,且点在一条直线上,连接分别为 的中点. (1)求证:①;②是等腰三角形. (2)在图①的基础上,将绕点按顺时针方向旋转,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立; (3)在(2)的条件下,请你在图②中延长交线段于点.求证:. C E N D A B M 图① C E M B D N 图② A B C F D P 图3 A B C D P 图2 E l l E F A B C D P 图1 l E F 13、在等边中,点为上一点,连结,直线与分别相交于点,且. (1)如图1,写出图中所有与相似的三角形,并选择其中一对给予证明; (2)若直线向右平移到图2、图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由; (3)探究:如图1,当满足什么条件时(其它条件不变),?请写出探究结果,并说明理由. 14、如图,已知:中,,将一块三角尺的直角顶点与斜边的中点重合,当三角尺绕着点旋转时,两直角边始终保持分别与边,交于 两点(不与重合). (1)求证:; (2)求四边形的面积; (3)若只将原题目中的“” 改为“”其它都不变, 请你探究:和还相等吗?如果相等, 请证明;如果不相等,请求出的值. 15、如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系: (1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系; ②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度 ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断. (2)将原题中正方形改为矩形(如图4—6),且AB=a,BC=b,CE=ka, CG=kb (ab,k0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由. (3)在第(2)题图5中,连结、,且a=3,b=2,k=,求的值. 16、如图,在平面直角坐标系中,的边在轴上,且,以为直径的圆过点.若点的坐标为,,A、B两点的横坐标,是关于的方程的两根. (1)求、的值; (2)若平分线所在的直线交轴于点, 试求直线对应的一次函数解析式; (3)过点任作一直线分别交射线、 (点除外)于点、.则的是 否为定值?若是,求出该定值;若不是,请说明理由. 17、如图,已知平面直角坐标系中的点,、为线段上两动点,过点作轴的平行线交轴于点,过点作轴的平行线交轴于点,交直线于点,且. (1) (填“>”、“=”、“<”),与的函数关系是 (不要求写自变量的取值范围); (2)当时,求的度数;(3)证明: 的度数为定值. 18、在梯形中,∥,,且.对角线相交于点,等腰直角三角板的直角顶点落在梯形的顶点上,使三角板绕点旋转。 (1)如图1,当三角板旋转到点落在边上时,线段与的位置关系是 ,数量关系是 ; (2)继续旋转三角板,旋转角为.请你在图2中画出图形,并判断(1)中结论还成立吗?如果成立请加以证明;如果不成立,请说明理由; (3)如图3,当三角板的一边与梯形对角线重合时,与相交于点P,若,求的长。 图1 图2 图3 18、(1)如图1,为的角平分线,于,于,,请补全图形,并求与的面积的比值; (2)如图2,分别以的边、为边向外作等边三角形和等边三角 形,与相交于点,判断与的数量关系,并证明; (3)在四边形中,已知,且,对角线平分, 请直接写出和的数量关系. 20、如图1,已知△是等腰直角三角形,,点是的中点.作 正方形,使点分别在和上,连接. (1)试猜想线段和的数量关系,请直接写出你得到的结论. (2)将正方形绕点逆时针方向旋转一定角度后(旋转角度大于,小于或 等于360°),如图2,通过观察或测量等方法判断(1)中的结论是否仍然 成立?如果成立,请予以证明;如果不成立,请说明理由. (3)若,在的旋转过程中,当为最大值时,求的值. A C B F D E G 图2 A C B F D E G 图1查看更多