天津市中考数学试卷及答案word解析版

天津市中考数学试卷及答案word解析版

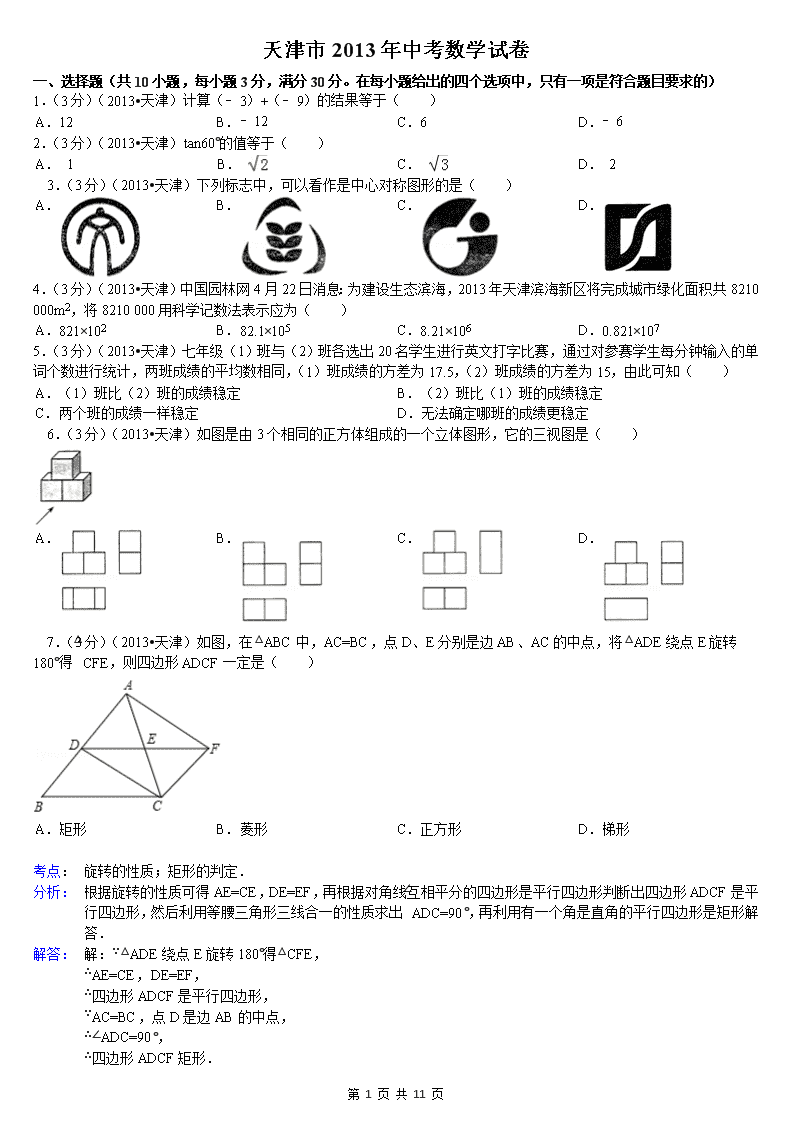
天津市2013年中考数学试卷 ‎ 一、选择题（共10小题，每小题3分，满分30分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．（3分）（2013•天津）计算（﹣3）+（﹣9）的结果等于（　　）‎ ‎　‎ A．‎ ‎12‎ B．‎ ‎﹣12‎ C．‎ ‎6‎ D．‎ ‎﹣6‎ ‎2．（3分）（2013•天津）tan60°的值等于（　　）[来#%源@:~中教^网]‎ ‎　‎ A．‎ ‎1‎ B．‎ C．‎ D．‎ ‎2‎ ‎　3．（3分）（2013•天津）下列标志中，可以看作是中心对称图形的是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎4．（3分）（2013•天津）中国园林网4月22日消息：为建设生态滨海，2013年天津滨海新区将完成城市绿化面积共8210 000m2，将8210 000用科学记数法表示应为（　　）‎ ‎　‎ A．‎ ‎821×102‎ B．‎ ‎82.1×105‎ C．‎ ‎8.21×106‎ D．‎ ‎0.821×107‎ ‎5．（3分）（2013•天津）七年级（1）班与（2）班各选出20名学生进行英文打字比赛，通过对参赛学生每分钟输入的单词个数进行统计，两班成绩的平均数相同，（1）班成绩的方差为17.5，（2）班成绩的方差为15，由此可知（　　）‎ ‎　‎ A．‎ ‎（1）班比（2）班的成绩稳定 B．‎ ‎（2）班比（1）班的成绩稳定 ‎　‎ C．‎ 两个班的成绩一样稳定 D．‎ 无法确定哪班的成绩更稳定 ‎　6．（3分）（2013•天津）如图是由3个相同的正方体组成的一个立体图形，它的三视图是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎　7．（3分）（2013•天津）如图，在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是（　　）‎ ‎　‎ A．‎ 矩形 B．‎ 菱形 C．‎ 正方形 D．‎ 梯形 考点：‎ 旋转的性质；矩形的判定．3718684‎ 分析：‎ 根据旋转的性质可得AE=CE，DE=EF，再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF是平行四边形，然后利用等腰三角形三线合一的性质求出∠ADC=90°，再利用有一个角是直角的平行四边形是矩形解答．‎ 解答：‎ 解：∵△ADE绕点E旋转180°得△CFE，‎ ‎∴AE=CE，DE=EF，‎ ‎∴四边形ADCF是平行四边形，‎ ‎∵AC=BC，点D是边AB的中点，‎ ‎∴∠ADC=90°，‎ ‎∴四边形ADCF矩形．‎ 第 11 页 共 11 页 故选A．‎ ‎8．（3分）（2013•天津）正六边形的边心距与边长之比为（　　）‎ ‎　‎ A．‎ ‎：3‎ B．‎ ‎：2‎ C．‎ ‎1：2‎ D．‎ ‎：2‎ ‎9．（3分）（2013•天津）若x=﹣1，y=2，则﹣的值等于（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎10．（3分）（2013•天津）如图，是一对变量满足的函数关系的图象，有下列3个不同的问题情境：‎ ‎①小明骑车以400米/分的速度匀速骑了5分，在原地休息了4分，然后以500米/分的速度匀速骑回出发地，设时间为x分，离出发地的距离为y千米；‎ ‎②有一个容积为6升的开口空桶，小亮以1.2升/分的速度匀速向这个空桶注水，注5分后停止，等4分后，再以2升/分的速度匀速倒空桶中的水，设时间为x分，桶内的水量为y升；‎ ‎③矩形ABCD中，AB=4，BC=3，动点P从点A出发，依次沿对角线AC、边CD、边DA运动至点A停止，设点P的运动路程为x，当点P与点A不重合时，y=S△ABP；当点P与点A重合时，y=0．‎ 其中，符合图中所示函数关系的问题情境的个数为（　　）‎ ‎　‎ A．‎ ‎0‎ B．‎ ‎1‎ C．‎ ‎2‎ D．‎ ‎3‎ 考点：‎ 函数的图象．3718684‎ 分析：‎ ‎①小明骑车以400米/分的速度匀速骑了5分，所走路程为2000米，与图象不符合；‎ ‎②小亮以1.2升/分的速度匀速向这个空桶注水，注5分后停止，注水量为1.2×5=6升，等4分钟，这段时间水量不变；再以2升/分的速度匀速倒空桶中的水，则3分钟后水量为0，符合函数图象；‎ ‎③当点P在AC上运动时，S△ABP的面积一直增加，当点P运动到点C时，S△ABP=6，这段时间为5，；当点P在CD上运动时，S△ABP不变，这段时间为4，；当点P在DA上运动时，S△ABP减小，这段时间为3，符合函数图象；‎ 解答：‎ 解：①小明骑车以400米/分的速度匀速骑了5分，所走路程为2000米，与图象不符合；‎ ‎②小亮以1.2升/分的速度匀速向这个空桶注水，注5分后停止，注水量为1.2×5=6升，等4分钟，这段时间水量不变；再以2升/分的速度匀速倒空桶中的水，则3分钟后水量为0，符合函数图象；‎ ‎③如图所示：‎ 当点P在AC上运动时，S△ABP的面积一直增加，当点P运动到点C时，S△ABP=6，这段时间为5，；当点P在CD上运动时，S△ABP不变，这段时间为4，；当点P在DA上运动时，S△ABP减小，这段时间为3，符合函数图象；‎ 综上可得符合图中所示函数关系的问题情境的个数为2．‎ 故选C．‎ ‎　‎ 二、填空题（共8小题，每小题3分，满分24分）‎ ‎11．（3分）（2013•天津）计算a•a6的结果等于　a7　．‎ ‎12．（3分）（2013•天津）一元二次方程x（x﹣6）=0的两个实数根中较大的根是　6　．‎ 第 11 页 共 11 页 ‎13．（3分）（2013•天津）若一次函数y=kx+1（k为常数，k≠0）的图象经过第一、二、三象限，则的取值范围是　k＞0　．‎ ‎14．（3分）（2013•天津）如图，已知∠C=∠D，∠ABC=∠BAD，AC与BD相交于点O，请写出图中一组相等的线段　AC=BD（答案不唯一）　．‎ 考点：‎ 全等三角形的判定与性质．3718684‎ 专题：‎ 开放型．‎ 分析：‎ 利用“角角边”证明△ABC和△BAD全等，再根据全等三角形对应边相等解答即可．‎ 解答：‎ 解：∵在△ABC和△BAD中，‎ ‎，‎ ‎∴△ABC≌△BAD（AAS），‎ ‎∴AC=BD，AD=BC．‎ 故答案为：AC=BD（答案不唯一）．‎ ‎15．（3分）（2013•天津）如图，PA、PB分别切⊙O于点A、B，若∠P=70°，则∠C的大小为　55　（度）．‎ ‎　16．（3分）（2013•天津）一个口袋中有四个完全相同的小球，把它们分别标号为1、2、3、4，随机地摸出一个小球，然后放回，再随机地摸出一个小球，则两次摸出的小球标号的和等于4的概率是　　．‎ ‎17．（3分）（2013•天津）如图，在边长为9的正三角形ABC中，BD=3，∠ADE=60°，则AE的长为　7　．‎ 考点：‎ 相似三角形的判定与性质；等边三角形的性质．3718684‎ 分析：‎ 先根据边长为9，BD=3，求出CD的长度，然后根据∠ADE=60°和等边三角形的性质，证明△ABD∽△DCE，进而根据相似三角形的对应边成比例，求得CE的长度，即可求出AE的长度．‎ 解答：‎ 解：∵△ABC是等边三角形，‎ ‎∴∠B=∠C=60°，AB=BC；‎ ‎∴CD=BC﹣BD=9﹣3=6；‎ ‎∴∠BAD+∠ADB=120°‎ ‎∵∠ADE=60°，‎ ‎∴∠ADB+∠EDC=120°，‎ ‎∴∠DAB=∠EDC，‎ 又∵∠B=∠C=60°，‎ 第 11 页 共 11 页 ‎∴△ABD∽△DCE，‎ 则=，‎ 即=，‎ 解得：CE=2，‎ 故AE=AC﹣CE=9﹣2=7．‎ 故答案为：7．‎ ‎18．（3分）（2013•天津）如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上．‎ ‎（Ⅰ）△ABC的面积等于　6　；‎ ‎（Ⅱ）若四边形DEFG是△ABC中所能包含的面积最大的正方形，请你在如图所示的网格中，用直尺和三角尺画出该正方形，并简要说明画图方法（不要求证明）　取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，则四边形DEFG即为所求　．‎ 考点：‎ 作图—相似变换；三角形的面积；正方形的性质．3718684‎ 专题：‎ 计算题．‎ 分析：‎ ‎（Ⅰ）△ABC以AB为底，高为3个单位，求出面积即可；‎ ‎（Ⅱ）作出所求的正方形，如图所示，画图方法为：取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，则四边形DEFG即为所求 解答：‎ 解：（Ⅰ）△ABC的面积为：×4×3=6；‎ ‎（Ⅱ）如图，取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，‎ 与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，‎ 则四边形DEFG即为所求．‎ 故答案为：（Ⅰ）6；（Ⅱ）取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，则四边形DEFG即为所求 点评：‎ 此题考查了作图﹣位似变换，三角形的面积，以及正方形的性质，作出正确的图形是解本题的关键．‎ ‎　‎ 三、解答题（共8小题，满分66分）‎ 第 11 页 共 11 页 ‎19．（6分）（2013•天津）解不等式组．‎ ‎20．（8分）（2013•天津）已知反比例函数y=（k为常数，k≠0）的图象经过点A（2，3）．‎ ‎（Ⅰ）求这个函数的解析式；‎ ‎（Ⅱ）判断点B（﹣1，6），C（3，2）是否在这个函数的图象上，并说明理由；‎ ‎（Ⅲ）当﹣3＜x＜﹣1时，求y的取值范围．‎ 考点：‎ 待定系数法求反比例函数解析式；反比例函数的性质；反比例函数图象上点的坐标特征．3718684‎ 分析：‎ ‎（1）把点A的坐标代入已知函数解析式，通过方程即可求得k的值．‎ ‎（Ⅱ）只要把点B、C的坐标分别代入函数解析式，横纵坐标坐标之积等于6时，即该点在函数图象上；‎ ‎（Ⅲ）根据反比例函数图象的增减性解答问题．‎ 解答：‎ 解：（Ⅰ）∵反比例函数y=（k为常数，k≠0）的图象经过点A（2，3），‎ ‎∴把点A的坐标代入解析式，得 ‎3=，‎ 解得，k=6，‎ ‎∴这个函数的解析式为：y=；‎ ‎（Ⅱ）∵反比例函数解析式y=，‎ ‎∴6=xy．‎ 分别把点B、C的坐标代入，得 ‎（﹣1）×6=﹣6≠6，则点B不在该函数图象上．‎ ‎3×2=6，则点C中该函数图象上；‎ ‎（Ⅲ）∵当x=﹣3时，y=﹣2，当x=﹣1时，y=﹣6，‎ 又∵k＞0，‎ ‎∴当x＜0时，y随x的增大而减小，‎ ‎∴当﹣3＜x＜﹣1时，﹣6＜y＜﹣2．‎ ‎21．（8分）（2013•天津）四川雅安发生地震后，某校学生会向全校1900名学生发起了“心系雅安”捐款活动，为了解捐款情况，学会生随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题：‎ ‎（Ⅰ）本次接受随机抽样调查的学生人数为　50　，图①中m的值是　32　；‎ ‎（Ⅱ）求本次调查获取的样本数据的平均数、众数和中位数；‎ ‎（Ⅲ）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．‎ 第 11 页 共 11 页 解答：‎ 解：（1）根据条形图4+16+12+10+8=50（人），‎ m=100﹣20﹣24﹣16﹣8=32；‎ ‎（2）∵=（5×4+10×16+15×12+20×10+30×8）=16，‎ ‎∴这组数据的平均数为：16，‎ ‎∵在这组样本数据中，10出现次数最多为16次，‎ ‎∴这组数据的众数为：10，‎ ‎∵将这组样本数据按从小到大的顺序排列，其中处于中间的两个数都是15，‎ ‎∴这组数据的中位数为：（15=15）=15；‎ ‎（3）∵在50名学生中，捐款金额为10元的学生人数比例为32%，‎ ‎∴由样本数据，估计该校1900名学生中捐款金额为10元的学生人数比例为32%，有1900×32%=608，‎ ‎∴该校本次活动捐款金额为10元的学生约有608名．‎ 故答案为：50，32．‎ ‎　‎ ‎22．（8分）（2013•天津）已知直线I与⊙O，AB是⊙O的直径，AD⊥I于点D．‎ ‎（Ⅰ）如图①，当直线I与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；‎ ‎（Ⅱ）如图②，当直线I与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．‎ 考点：‎ 切线的性质；圆周角定理；直线与圆的位置关系．3718684‎ 分析：‎ ‎（Ⅰ）如图①，首先连接OC，根据当直线l与⊙O相切于点C，AD⊥l于点D．易证得OC∥AD，继而可求得∠BAC=∠DAC=30°；‎ ‎（Ⅱ）如图②，连接BF，由AB是⊙O的直径，根据直径所对的圆周角是直角，可得∠AFB=90°，由三角形外角的性质，可求得∠AEF的度数，又由圆的内接四边形的性质，求得∠B的度数，继而求得答案．‎ 解答：‎ 解：（Ⅰ）如图①，连接OC，‎ ‎∵直线l与⊙O相切于点C，‎ ‎∴OC⊥l，‎ ‎∵AD⊥l，‎ ‎∴OC∥AD，‎ ‎∴∠OCA=∠DAC，‎ ‎∵OA=OC，‎ ‎∴∠BAC=∠OCA，‎ ‎∴∠BAC=∠DAC=30°；‎ ‎（Ⅱ）如图②，连接BF，‎ ‎∵AB是⊙O的直径，‎ ‎∴∠AFB=90°，‎ ‎∴∠BAF=90°﹣∠B，‎ ‎∴∠AEF=∠ADE+∠DAE=90°+18°=108°，‎ 在⊙O中，四边形ABFE是圆的内接四边形，‎ 第 11 页 共 11 页 ‎∴∠AEF+∠B=180°，‎ ‎∴∠B=180°﹣108°=72°，‎ ‎∴∠BAF=90°﹣∠B=180°﹣72°=18°．‎ ‎　‎ ‎23．（8分）（2013•天津）天塔是天津市的标志性建筑之一，某校数学兴趣小组要测量天塔的高度，如图，他们在点A处测得天塔最高点C的仰角为45°，再往天塔方向前进至点B处测得最高点C的仰角为54°，AB=112m，根据这个兴趣小组测得的数据，计算天塔的高度CD（tan36°≈0.73，结果保留整数）．‎ 考点：‎ 解直角三角形的应用-仰角俯角问题．3718684‎ 分析：‎ 首先根据题意得：∠CAD=45°，∠CBD=54°，AB=112m，在Rt△ACD中，易求得BD=AD﹣AB=CD﹣112；在Rt△BCD中，可得BD=CD•tan36°，即可得CD•tan36°=CD﹣112，继而求得答案．‎ 解答：‎ 解：根据题意得：∠CAD=45°，∠CBD=54°，AB=112m，‎ ‎∵在Rt△ACD中，∠ACD=∠CAD=45°，‎ ‎∴AD=CD，‎ ‎∵AD=AB+BD，‎ ‎∴BD=AD﹣AB=CD﹣112（m），‎ ‎∵在Rt△BCD中，tan∠BCD=，∠BCD=90°﹣∠CBD=36°，‎ ‎∴tan36°=，‎ ‎∴BD=CD•tan36°，‎ ‎∴CD•tan36°=CD﹣112，‎ ‎∴CD=≈≈415（m）．‎ 答：天塔的高度CD为：415m．‎ ‎24．（8分）（2013•天津）甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费，设小红在同一商场累计购物x元，其中x＞100．‎ ‎（1）根据题题意，填写下表（单位：元）‎ 累计购物 实际花费 ‎130‎ ‎290‎ ‎…‎ x 在甲商场 ‎127‎ ‎…‎ 第 11 页 共 11 页 在乙商场 ‎126‎ ‎…‎ ‎（2）当x取何值时，小红在甲、乙两商场的实际花费相同？‎ ‎（3）当小红在同一商场累计购物超过100元时，在哪家商场的实际花费少？‎ 解答：‎ 解：（1）在甲商场：100+（290﹣100）×0.9=271，‎ ‎100+（290﹣100）×0.9x=0.9x+10；‎ 在乙商场：50+（290﹣50）×0.95=278，‎ ‎50+（290﹣50）×0.95x=0.95x+2.5；‎ ‎（2）根据题意得出：‎ ‎0.9x+10=0.95x+2.5，‎ 解得：x=150，‎ ‎∴当x=150时，小红在甲、乙两商场的实际花费相同，‎ ‎（3）由0.9x+10＜0.95x+2.5，‎ 解得：x＞150，‎ ‎0.9x+10＞0.95x+2.5，‎ 解得：x＜150，‎ yB=0.95x+50（1﹣95%）=0.95x+2.5，正确；‎ ‎∴当小红累计购物大于150时上没封顶，选择甲商场实际花费少；‎ 当小红累计购物超过100元而不到150元时，在乙商场实际花费少．‎ ‎25．（10分）（2013•天津）在平面直角坐标系中，已知点A（﹣2，0），点B（0，4），点E在OB上，且∠OAE=∠0BA．‎ ‎（Ⅰ）如图①，求点E的坐标；‎ ‎（Ⅱ）如图②，将△AEO沿x轴向右平移得到△A′E′O′，连接A′B、BE′．‎ ‎①设AA′=m，其中0＜m＜2，试用含m的式子表示A′B2+BE′2，并求出使A′B2+BE′2取得最小值时点E′的坐标；‎ ‎②当A′B+BE′取得最小值时，求点E′的坐标（直接写出结果即可）．‎ 解答：‎ 解：（Ⅰ）如图①，∵点A（﹣2，0），点B（0，4），‎ ‎∴OA=2，OB=4．‎ ‎∵∠OAE=∠0BA，∠EOA=∠AOB=90°，‎ ‎∴△OAE∽△OBA，‎ ‎∴=，即=，‎ 解得，OE=1，‎ ‎∴点E的坐标为（0，1）；‎ ‎（Ⅱ）①如图②，连接EE′．‎ 由题设知AA′=m（0＜m＜2），则A′O=2﹣m．‎ 在Rt△A′BO中，由A′B2=A′O2+BO2，得A′B2=（2﹣m）2+42=m2﹣4m+20．‎ 第 11 页 共 11 页 ‎∵△A′E′O′是△AEO沿x轴向右平移得到的，‎ ‎∴EE′∥AA′，且EE′=AA′．‎ ‎∴∠BEE′=90°，EE′=m．‎ 又BE=OB﹣OE=3，‎ ‎∴在Rt△BE′E中，BE′2=E′E2+BE2=m2+9，‎ ‎∴A′B2+BE′2=2m2﹣4m+29=2（m﹣1）2+27．‎ 当m=1时，A′B2+BE′2可以取得最小值，此时，点E′的坐标是（1，1）．‎ ‎②如图②，过点A作AB′⊥x，并使AB′=BE=3．‎ 易证△AB′A′≌△EBE′，‎ ‎∴B′A=BE′，‎ ‎∴A′B+BE′=A′B+B′A′．‎ 当点B、A′、B′在同一条直线上时，A′B+B′A′最小，即此时A′B+BE′取得最小值．‎ 易证△AB′A′∽△OBA′，‎ ‎∴==，‎ ‎∴AA′=×2=，‎ ‎∴EE′=AA′=，‎ ‎∴点E′的坐标是（，1）．‎ ‎26．（10分）（2013•天津）已知抛物线y1=ax2+bx+c（a≠0）的对称轴是直线l，顶点为点M．若自变量x和函数值y1的部分对应值如下表所示：‎ ‎（Ⅰ）求y1与x之间的函数关系式；‎ ‎（Ⅱ）若经过点T（0，t）作垂直于y轴的直线l′，A为直线l′上的动点，线段AM的垂直平分线交直线l于点B，点B关于直线AM的对称点为P，记P（x，y2）．‎ ‎（1）求y2与x之间的函数关系式；‎ ‎（2）当x取任意实数时，若对于同一个x，有y1＜y2恒成立，求t的取值范围．‎ x ‎…‎ ‎﹣1‎ ‎0‎ ‎3‎ ‎…‎ y1=ax2+bx+c ‎…‎ ‎0‎ ‎0‎ ‎…‎ 分析：‎ ‎（II）先根据（I）中y1与x之间的函数关系式得出顶点M的坐标．‎ 第 11 页 共 11 页 ‎①记直线l与直线l′交于点C（1，t），当点A′与点C不重合时，由已知得，AM与BP互相垂直平分，故可得出四边形ANMP为菱形，所以PA∥l，再由点P（x，y2）可知点A（x，t）（x≠1），所以PM=PA=|y2﹣t|，过点P作PQ⊥l于点Q，则点Q（1，y2），故QM=|y2﹣3|，PQ=AC=|x﹣1|，在Rt△PQM中，根据勾股定理即可得出y2与x之间的函数关系式，再由当点A与点C重合时，点B与点P重合可得出P点坐标，故可得出y2与x之间的函数关系式；‎ ‎②据题意，借助函数图象：当抛物线y2开口方向向上时，可知6﹣2t＞0，即t＜3时，抛物线y1的顶点M（1，3），抛物线y2的顶点（1，），由于3＞，所以不合题意，当抛物线y2开口方向向下时，6﹣2t＜0，即t＞3时，求出y1﹣y2的值；若3t﹣11≠0，要使y1＜y2恒成立，只要抛物线方向及且顶点（1，）在x轴下方，因为3﹣t＜0，只要3t﹣11＞0，解得t＞，符合题意；若3t﹣11=0，y1﹣y2=﹣＜0，即t=也符合题意．‎ 解答：‎ 解：（Ⅰ）∵抛物线经过点（0，），‎ ‎∴c=． ∴y1=ax2+bx+，‎ ‎∵点（﹣1，0）、（3，0）在抛物线y1=ax2+bx+上，‎ ‎∴，解得，‎ ‎∴y1与x之间的函数关系式为：y1=﹣x2+x+；‎ ‎（II）∵y1=﹣x2+x+，‎ ‎∴y1=﹣（x﹣1）2+3，‎ ‎∴直线l为x=1，顶点M（1，3）．‎ ‎①由题意得，t≠3，‎ 如图，记直线l与直线l′交于点C（1，t），当点A′与点C不重合时，‎ ‎∵由已知得，AM与BP互相垂直平分，‎ ‎∴四边形ANMP为菱形，‎ ‎∴PA∥l，‎ 又∵点P（x，y2），‎ ‎∴点A（x，t）（x≠1），‎ ‎∴PM=PA=|y2﹣t|，‎ 过点P作PQ⊥l于点Q，则点Q（1，y2），‎ ‎∴QM=|y2﹣3|，PQ=AC=|x﹣1|，‎ 在Rt△PQM中，‎ ‎∵PM2=QM2+PQ2，即（y2﹣t）2=（y2﹣3）2+（x﹣1）2，整理得，y2=（x﹣1）2+，‎ 即y2=x3﹣x+，‎ ‎∵当点A与点C重合时，点B与点P重合，‎ ‎∴P（1，）， ∴P点坐标也满足上式，‎ 第 11 页 共 11 页 ‎∴y2与x之间的函数关系式为y2=x3﹣x+（t≠3）；‎ ‎②根据题意，借助函数图象：‎ 当抛物线y2开口方向向上时，6﹣2t＞0，即t＜3时，抛物线y1的顶点M（1，3），抛物线y2的顶点（1，），‎ ‎∵3＞，‎ ‎∴不合题意，‎ 当抛物线y2开口方向向下时，6﹣2t＜0，即t＞3时，‎ y1﹣y2=﹣（x﹣1）2+3﹣[（x﹣1）2+]‎ ‎=（x﹣1）2+，‎ 若3t﹣11≠0，要使y1＜y2恒成立，‎ 只要抛物线y=（x﹣1）2+开口方向向下，且顶点（1，）在x轴下方，‎ ‎∵3﹣t＜0，只要3t﹣11＞0，解得t＞，符合题意；‎ 若3t﹣11=0，y1﹣y2=﹣＜0，即t=也符合题意．‎ 综上，可以使y1＜y2恒成立的t的取值范围是t≥．‎ 第 11 页 共 11 页