- 2021-05-10 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
河北省沧州市第一中学2020年高三数学寒假作业3
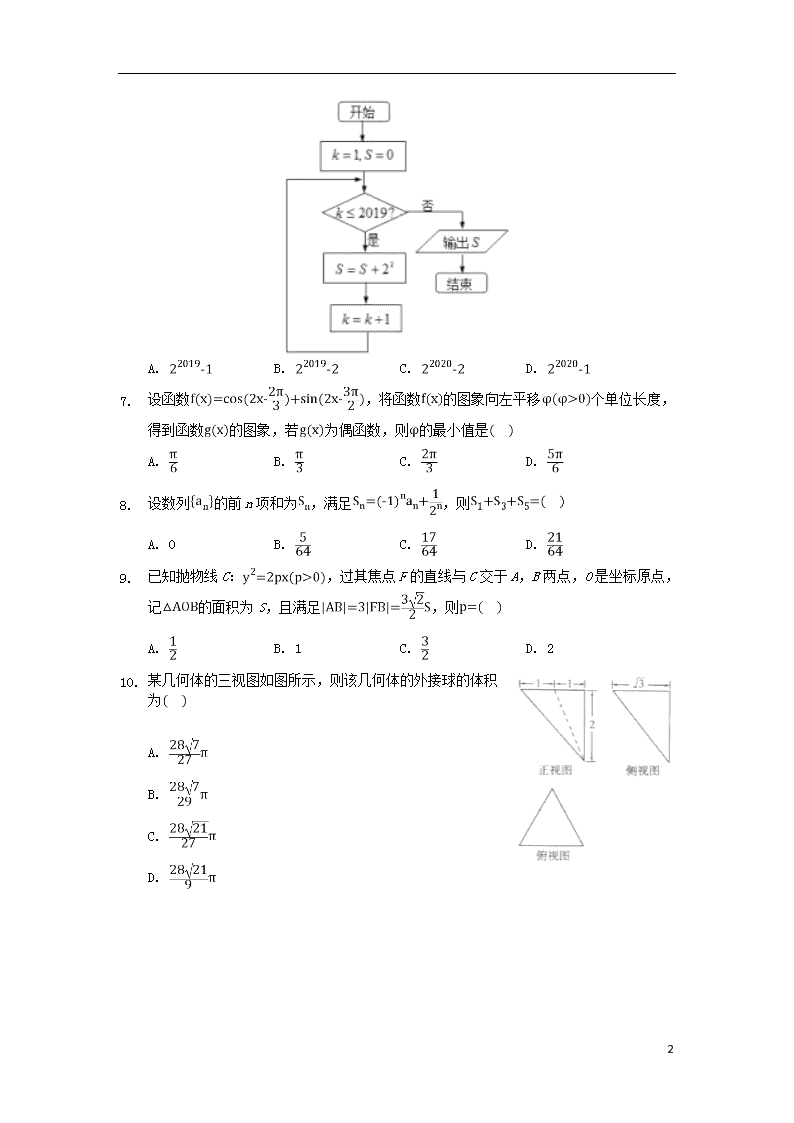
1 河北省沧州市第一中学 2020 年高三数学寒假作业 3 一、选择题(本大题共 12 小题,共 36.0 分) 1. 已知复数 ,则复数 的虚部为 A. 1 B. C. i D. 2. 已知集合 , ,则 A. B. C. D. 3. 设 , 均为单位向量,当 , 的夹角为 时, 在 方向上的投影为 A. B. C. D. 4. 已知等差数列 满足 ,则 中一定为零的项是 A. B. C. D. 5. 新高考方案规定,普通高中学业水平考试分为合格性考试 合格考 和选择性考试 选择 考 其中“选择考”,成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原 始卷面分数,由高到低进行排序,评定为 A、B、C、D、E 五个等级,某试点高中 2018 年参加“选择考”总人数是 2016 年参加“选择考”总人数的 2 倍,为了更好地分析该 校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果, 得到:如图表 针对该校“选择考”情况,2018 年与 2016 年比较,下列说法正确的是 A. 获得 A 等级的人数减少了 B. 获得 B 等级的人数增加了 倍 C. 获得 D 等级的人数减少了一半 D. 获得 E 等级的人数相同 6. 执行如图所示的程序框图,输出的结果为 2 A. B. C. D. 7. 设函数 ,将函数 的图象向左平移 个单位长度, 得到函数 的图象,若 为偶函数,则 的最小值是 A. B. C. D. 8. 设数列 的前 n 项和为 ,满足 ,则 A. 0 B. C. D. 9. 已知抛物线 C: ,过其焦点 F 的直线与 C 交于 A,B 两点,O 是坐标原点, 记 的面积为 S,且满足 ,则 A. B. 1 C. D. 2 10. 某几何体的三视图如图所示,则该几何体的外接球的体积 为 A. B. C. D. 3 11. 已知函数 的图象上有且仅有四个不同的点关于直线 的对称点 在 的图象上,则实数 k 的取值范围是 A. B. C. D. 12. 在 中,A,B、C 为其三内角,满足 tanA,tanB、tanC 都是整数,且 ,则 下列结论中错误的是 A. B. C. D. 二、填空题(本大题共 4 小题,共 20.0 分) 13. 已知 ,则 ______. 14. 已知双曲线 C: 的左、右焦点分别为 , ,以线段 为直径的圆 交 C 的一条渐近线于点 在第一象限内 ,若线段 的中点 Q 在 C 的另一条渐近线上, 则 C 的离心率 ______. 15. 中国光谷 武汉 某科技公司生产一批同型号的光纤通讯仪器, 每台仪器的某一部件由三个电子元件按如图方式连接面成,若 元件 1 或元件 2 正常工作,且元件 3 正常工作,则该部件正常 工作,由大数据统计显示:三个电子元件的使用寿命 单位:小时 均服从正态分布 ,且各个元件能否正常工作相互独立.现从这批仪器中随机抽取 1000 台 检测该部件的工作情况 各部件能否正常工作相互独立 ,那么这 1000 台仪器中该部件 的使用寿命超过 10000 小时的平均值为______台 16. 已知正方体 的棱长为 2,P 为体对角线 上的一点,且 ,现有以下判断, 若 平画 PAC,则 周 长的最小值是 若 为钝角三角形,则 的取值范国为 其中正确判断 的序号为______. 三、解答题(本大题共 7 小题,共 82.0 分) 17. 在 中, ,AD 是 的内角平分线,点 D 在线段 BC 上,且 . 求 sinB 的值; 若 ,求 的面积 18. 如图,等腰梯形 ABCD 中, , , ,E 为 CD 中点,以 AE 为折 痕把 折起,使点 D 到达点 P 的位置 平面 . 4 Ⅰ 证明: ; Ⅱ 若直线 PB 与平面 ABCE 所成的角为 ,求二面角 的余弦值. 19. 已知点 在椭圆 C: 上,且点 M 到 C 的左、右焦点的距离之 和为 求 C 的方程 设 O 为坐标原点,若 C 的弦 AB 的中点在线段 不含端点 O, 上,求 的取 值范围 20. 武汉有“九省通衢”之称,也称为“江城”,是国家历史文化名城,其中著名的景点有 黄鹤楼、户部巷、东湖风量区等等 为了解“五 一”劳动节当日江城某旅游景点游客年龄的分布情况,从年龄在 22 岁 到 52 岁的游客中随机抽取了 1000 人,制成了如下的频率分布直方图: 现从年龄在 内的游客中,采用分层抽样的方法抽取 10 人,再从抽取的 10 人中 随机抽取 4 人,记 4 人中年龄在 内的人数为 ,求 为了给游客提供更舒适的旅的体验,该旅游景点游船中心计划在 2020 年劳动节当日 投人至少 1 艘至多 3 艘型游船供游客乘坐观光,由 2010 到 2019 这 10 年间的数据资料 显示每年劳动节当日客流量 单位:万人 都大于 将每年劳动节当日客流量数据分成 3 个区间整理得如表 劳动节当日客流量 X 频数 年 2 4 4 5 以这 10 年的数据资料记录的 3 个区间客流量的频率作为每年客流量在该区间段发生的 概率,且每年劳动节当日客流量相互独立. 该游船中心希望投入的 A 型游船尽可能被充分利用,但每年劳动节当日 A 型游船最多使 用量 单位艘 要受当日客流量 单位:万人 的影响,其关联关系如表 劳动节当日客流量 X A 型游船最多使用量 1 2 3 若某艘 A 型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润 3 万元;若 某艘 A 型游船劳动节当日被投入却不被使用,则游船中心当日亏损 万元记 单位: 万元 表示该游船中心在劳动节当日获得的总利润,Y 的数学期望越大游船中心在劳动 节当日获得的总利润越大,问该游船中心在 2020 年劳动节当日应投人多少艘 A 型游船 才能使其当日获得的总利润最大. 21. 已知函数 , 讨论 极值点的个数 若 是 的一个极值点,且 ,证明: . 22. 在平面直角坐标系 xOy 中,曲线 C 的参数方程为 为参数 ,在以原点为极点, x 轴正半轴为轴的坐标系中,直线 l 的极坐标方程为 . 求曲线 C 的普通方程和直线 l 的直角坐标方程; 6 设点 ,直线 l 和曲线 C 交于 A,B 两点,求 的值. 23. 已知函数 . 当 时,求不等式 的解集; 若不等式 对任意的 恒成立,求 a 的取值范围. 7 答案和解析 1.【答案】A 【解析】解:由 ,得 . 则复数 的虚部为 1. 故选:A. 直接利用复数代数形式的乘除运算化简得答案. 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题. 2.【答案】C 【解析】解: 集合 , , 故选:C. 先分别求出集合 A,B,由此能求出 . 本题考查交集的求法,考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础 题. 3.【答案】B 【解析】解:因为 , 均为单位向量,且 , 的夹角为 , 所以 在 方向上的投影为: , 故选:B. 在 方向上的投影为 ,代入数值计算即可. 本题考查了平面向量投影的计算,属基础题. 4.【答案】A 【解析】【分析】 本题考查了等差数列的通项公式,考查了推理能力与计算能力,属于基础题. 利用通项公式即可得出. 【解答】 解:设等差数列 的公差为 d, , ,可得: , , 则 中一定为零的项是 . 8 故选 A. 5.【答案】B 【解析】【分析】 本题考查了频率分布直方图和扇形图的应用问题,也考查了频率、频数与样本容量的应用问 题,是基础题. 根据频率分布直方图扇形图,利用频率与样本容量的关系即可解答. 【解答】 解:由题可知:设 2016 年参加选择考的总人数为:a 人;则:2018 年参加选择考的总人数 为:2a 人; 2016 年评定为 A、B、C、D、E 五个等级的人数为: A: 、B: 、C: 、D: 、E: ; 2018 年评定为 A、B、C、D、E 五个等级的人数为:A: 、B: 、C: 、D: 、 E: ; 对各个选项进行比较可得 B 正确. 故选:B. 6.【答案】C 【解析】解:模拟程序的运行,可得该程序的功能是利用循环结构计算并输出变量 的值, 由于 . 故选:C. 由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量 的值,利用等比数列的求和公式即可计算得解. 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论, 是基础题. 7.【答案】A 【解析】解:函数 , , 将函数 的图象向左平移 个单位长度, 得到函数 的图象, 由于 为偶函数, 故: , 解得: , 当 时, 的最小值为 . 故选:A. 9 首先利用三角函数关系式的恒等变换,把函数的关系式变形成正弦型函数,进一步利用平移 变换和伸缩变换的应用和性质求出结果. 本题考查的知识要点:三角函数关系式的变换,函数的图象的平移变换和伸缩变换的应用, 主要考察学生的运算能力和转换能力,属于基础题型. 8.【答案】D 【解析】【分析】 直接利用函数的关系式的应用和偶函数的性质的应用求出结果. 本题考查的知识要点:函数的关系式的应用,偶函数的性质的应用,主要考察学生的运算能 力和转换能力,属于基础题型. 【解答】 解:数列 的前 n 项和为 ,满足 , 则:当 n 为偶数时, , 所以: . 故选:D. 9.【答案】D 【解析】解:设直线 AB 的方程为: ,将其代入抛物线 C 的方程得: , 设 , , 则 , , 又 , , , , 联立 可得 , 由弦长公式得 , ,解得: . 故选:D. 联立直线与抛物线,根据韦达定理以及面积公式烈士可得. 本题考查了抛物线的性质,属中档题. 10.【答案】C 【解析】解:根据几何体的三视图转换为几何体为: 如图所示: 10 所以: , 故: , 所以: . 故选:C. 首先把三视图转换为几何体,进一步求出外接球的半径,进一步求出球的体积. 本题考查的知识要点:三视图和几何体之间的转换,几何体的体积公式的应用,主要考察学 生的运算能力和转换能力,属于基础题型. 11.【答案】A 【解析】 【分析】 由题意可化为函数 图象与 的图象有且只有四个不同的交点,结 合题意作图求解即可. 本题考查了函数的性质的判断与应 用,同时考查了学生的作图能力及数 形结合的思想应用. 【解答】 解: 函数 的图象上 有且仅有四个不同的点关于直线 的对称点在 的图象上, 而函数 关于直线 的对称图象为 , 的图象与 的图象有且只有四个不同的交点. 作函数 的图象与 的图象如下, 易知直线 恒过点 , 设直线 AC 与 相切于点 , , 11 故 , 解得, ; 故 . 设直线 AB 与 相切于点 , , 故 , 解得, . 故 ; 故 , 故 . 故选 A. 12.【答案】A 【解析】解: 中,由于 , 所以 B,C 都是锐角, 由于 tanB,tanC 都是整数, 由 ,得 , 可得 A 也为锐角, 这时, , , , 可得: ,即 , 由于: , ,比较可知只可能 , , , 由于: ,可知 ,故 B 正确; 由于: ,可知 , 又 ,故选项 C 正确; 又由于 ,可得选项 D 正确; 故选:A. 由题意易得 B,C 都是锐角,利用诱导公式,两角和的正切函数公式可求 , 可得 A 也为锐角,由 , , ,可得 ,结合 , ,比较可知只可能 , , ,逐项分析即可得解. 12 本题主要考查了两角和的正切公式,诱导公式的应用问题,体现了分类讨论的数学思想方法, 属中档题. 13.【答案】10 【解析】解: , 则 展开式的通项为 , 令 得 , 故答案为:10. 由二项式定理及展开式通项公式得: 展开式的通项为 ,令 得 ,得解. 本题考查了二项式定理及展开式通项公式,属简单题. 14.【答案】2 【解析】解:如图:因为 Q,O 分别是 , 的 中点,所以 , 为圆的直径, , 直线 的方程为: 与 联立解得 , 根据中点公式得 ,将其代入 得: , , . 故答案为:2. 如图:因为 Q,O 分别是 , 的中点,所以 , 为圆的直径, ,再根据直线 的方程与 联立得 Q 的坐标,根据中点公 式得 P 的坐标,将其代入 可得 ,可得离心率. 本题考查了双曲线的性质,属中档题. 15.【答案】375 【解析】解:三个电子元件的使用寿命均服从正态分布 , 得:三个电子元件的使用寿命超过 10000 小时的概率为 , 设 超过 10000 小时时,元件 1、元件 2 至少有一个正常 , 超过 10000 小时时,元件 3 正常 , 该部件的使用寿命超过 10000 小时 . 13 则 , , 事件 A,B 为相互独立事件,事件 C 为 A、B 同时发生的事件, . 这 1000 台仪器中该部件的使用寿命超过 10000 小时的平均值为 . 故答案为:375. 先根据正态分布的意义,知三个电子元件的使用寿命超过 10000 小时的概率为 ,而所求事 件“该部件的使用寿命超过 10000 小时”当且仅当“超过 10000 小时时, 元件 1、元件 2 至少有一个正常”和“超过 10000 小时,元件 3 正常”同时发生,由于其为 独立事件,故分别求其概率再相乘,最后乘以 1000 得答案. 本题主要考查了正态分布的意义,独立事件同时发生的概率运算,对立事件的概率运算等基 础知识,是中档题. 16.【答案】 【解析】解:对于 , 面 , 面 , , 正确; 对于 ,若 平面 PAC,几何体是正方体, 在 平面 中,则 , 正确; 对于 ,建立空间直角坐标系,如图所示,设 x, , , 0, , 2, ; , 的周长最小值为 , 错误; 对于 ,建立空间直角坐标系,不妨设正方体的棱长 , 则 0, , 1, , 1, , 0, , 0, , 1, , 1, , 0, , , , , , 显然 不是平角,所以 为钝角等价于 , , 等价于 , 即 , 故 , 正确; 故答案为: . 根据空间中的垂直关系,即可判断 的正误; 利用正方体的特征,判断 平面 PAC 时对应 的值即可; 14 建立空间直角坐标系,即可求得 周长的最小值; 通过建立空间直角坐标系,求出 为钝角三角形时 的取值范围. 本题考查空间直角坐标系的应用,夹角与距离的关系,考查空间想象能力以及计算能力. 17.【答案】解: 在 中,由正弦定理可得: ,即: , 在 中,由正弦定理可得: ,即 , 两式子相除可得: ,即 , 可得: ,即 , 又 , 可得: . 由 ,可得 B 是锐角,于是 , 所以 , 在 中,由正弦定理可得: , 于是 , 所以 . 【解析】 在 中,由正弦定理可得 ,在 中,由正弦定理可得 ,两式相除可得 ,结合范围 ,利用同角三角函数基本关系式 可求 sinB 的值. 由同角三角函数基本关系式可求 cosB,利用两角和的正弦函数公式可求 ,在 中,由正弦定理可得 AB 的值,可求 的值,根据三角形的面积公式即可计 算得解. 本题主要考查了正弦定理,同角三角函数基本关系式,两角和的正弦函数公式,三角形的面 积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题. 18.【答案】 证明:连接 BD,设 AE 的中点为 O, , , 四边形 ABCE 为平行四边形, , , 为等边三角形, , , 又 ,OP, 平面 POB, 平面 POB,又 平面 POB, . 15 解:在平面 POB 内作 平面 ABCE,垂足为 Q,则 Q 在直线 OB 上, 直线 PB 与平面 ABCE 夹角为 , 又 , , 、Q 两点重合,即 平面 ABCE, 以 O 为原点,OE 为 x 轴,OB 为 y 轴,OP 为 z 轴,建立空间直角坐标系, 则 0, , 0, , , 0, , , 设平面 PCE 的一个法向量为 y, , 则 ,即 , 令 得 , 又 平面 PAE, 1, 为平面 PAE 的一个法向量, 设二面角 为 , 则 , 易知二面角 为钝角,所以 . 【解析】本题考查了线面垂直的判定与性质,考查空间向量与二面角的计算,属于中档题. 连接 BD,设 AE 的中点为 O,可证 , ,故而 平面 POB,于是 ; 证明 ,建立空间坐标系,求出两平面的法向量,计算法向量的夹角得出二面角的 大小. 19.【答案】解: 由题意可得: , ,解得 , . 椭圆的标准方程为: . 设 , 直线 OM 的方程为: 弦 AB 的中点在线段 不含端点 O, 上, ,化为: 由 , ,相减可得: . 16 , . . 设直线 AB 的方程为: ,代入椭圆方程可得: . 解得 . 又 , . 由根与系数的关系可得: , . -- . 而 . . 【解析】 由题意可得: , ,解得 a, 即可得出椭圆的标准方程. 设 , 直线 OM 的方程为: 弦 AB 的中点在线段 不含端点 O, 上, 可得 由 , ,相减可得: 设直线 AB 的方程为: ,代入椭圆方程可得: 解得 把根与系数的关系代入 化简即可得出. 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、中点坐标公式、斜 率计算公式、不等式的解法、向量数量积运算性质,考查了推理能力与计算能力,属于难题. 20.【答案】解: 年龄在 内的游客人数为 150,年龄在 内的游客人数为 100, 若采用分层抽样的方法抽取 10 人,则年龄在 内的人数为 6 人, 年龄在 内的人数为 4 人, . 当投入 1 艘 A 型游船时,因客流量总大于 1,则 万元 , 当投入 2 艘 A 型游船时, 若 ,则 , 此时 , 若 ,则 , 此时 , 此时,Y 的分布列为: Y 6 17 P 此时 万元 . 当投入 3 艘 A 型游船时, 若 ,则 ,此时 , 若 ,则 , 此时 , 若 ,则 ,此时 , 此时,Y 的分布列如下表: Y 2 9 P 此时, 万元 . 由于 , 则该游艇船中心在 2020 年劳动节当时应投入 3 艘 A 型游船使其当时获得的总利润最大. 【解析】 采用分层抽样的方法抽取 10 人,则年龄在 内的人数为 6 人,由此能求 出年龄在 内的人数为 4 人, 的值. 当投入 1 艘 A 型游船时,因客流量总大于 1,则 万元 ,当投入 2 艘 A 型游船时, 求出 Y 的分布列,从而 万元 当投入 3 艘 A 型游船时,求出 Y 的分布 列,从而 万元 ,由此能求出该游艇船中心在 2020 年劳动节当 时应投入 3 艘 A 型游船使其当时获得的总利润最大. 本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法,考查古典概型等基 础知识,考查推理能力与计算能力,是中档题. 21.【答案】 解: 的定义域为 R, ; 若 ,则 ; 当 时, , 单调递减;当 时, , 单调递增; 是 唯一的极小值点,无极大值点,故此时 有 1 个极值点; 若 ,令 ,则 , ; 当 时, ,可知当 时, ;当 时, ; , 分别是 的极大值点和极小值点,故此时 有 2 个极值点; 当 时, , ,此时 在 R 上单调递增,无极值点; 当 时, ,同理可知, 有 2 个极值点; 综上,当 时, 无极值点;当 时, 有 1 个极值点;当 或 时, 有 2 个极值点 证明:若 是 的一个极值点,由 知 ; 又 ; 18 ; 则 ; ; 令 ,则 ; ; ; 又 ; ; 令 ,得 ; 当 时, , 单调递增; 当 时, , 单调递减; 是 唯一得极大值点,也是最大值点,即 ; ,即 . 【解析】 对 求导,对于 a 的取值进行分类讨论,进而得出 的增减性与极值点的个 数; 根据题目条件和第 问,确定 a 的范围,得到 的表达式,再利用换元法令 , 求出函数 的最大值,从而得证 . 本题考查了利用导数求函数的单调区间、极值,涉及转化思想,分类讨论,换元法,属难题. 22.【答案】解: 由 消去参数 ,得 ,即曲线 C 的普通方程为: , 由 ,得 ,化为直角坐标方程为: . 由 知,点 在直线 l 上,可设直线 l 的参数方程为 为参数 , 即 为参数 ,代入 并化简得 , ,设 A,B 两点对应的参数分别为 , ,得 , , 所以 , 所以 . 【解析】 消去参数 可得曲线 C 的普通方程;根据互化公式可得直线 l 的直角坐标方程; 根据参数 t 的几何意义可得. 本题考查了参数方程化成普通方程,属中档题. 23.【答案】解: 当 时, , 等价于 或 或 , 19 解得 或 , 不等式的解集为 或 ; 当 时,由 得 即 , 或 对任意的 恒成立, 又 , , 或 ,又 , , 的取值范围为: . 【解析】 将 代入 中,去绝对值,然后分别解不等式; 由条件可得 ,即 或 对任意的 恒成立,然后解出 a 的范围即 可. 本题考查了绝对值不等式的解法和绝对值不等式恒成立问题,属基础题.查看更多