北师大版数学七年级下册第三章《表示变量关系》检测题

北师大版数学七年级下册第三章《表示变量关系》检测题

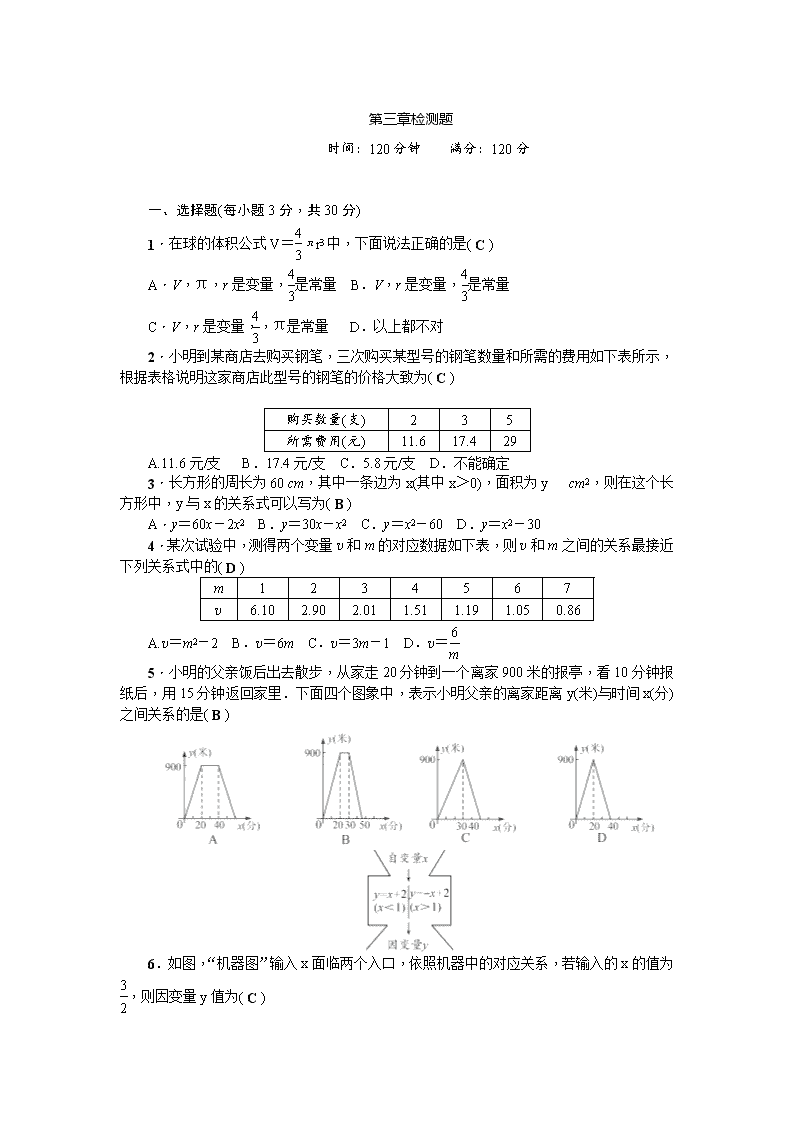
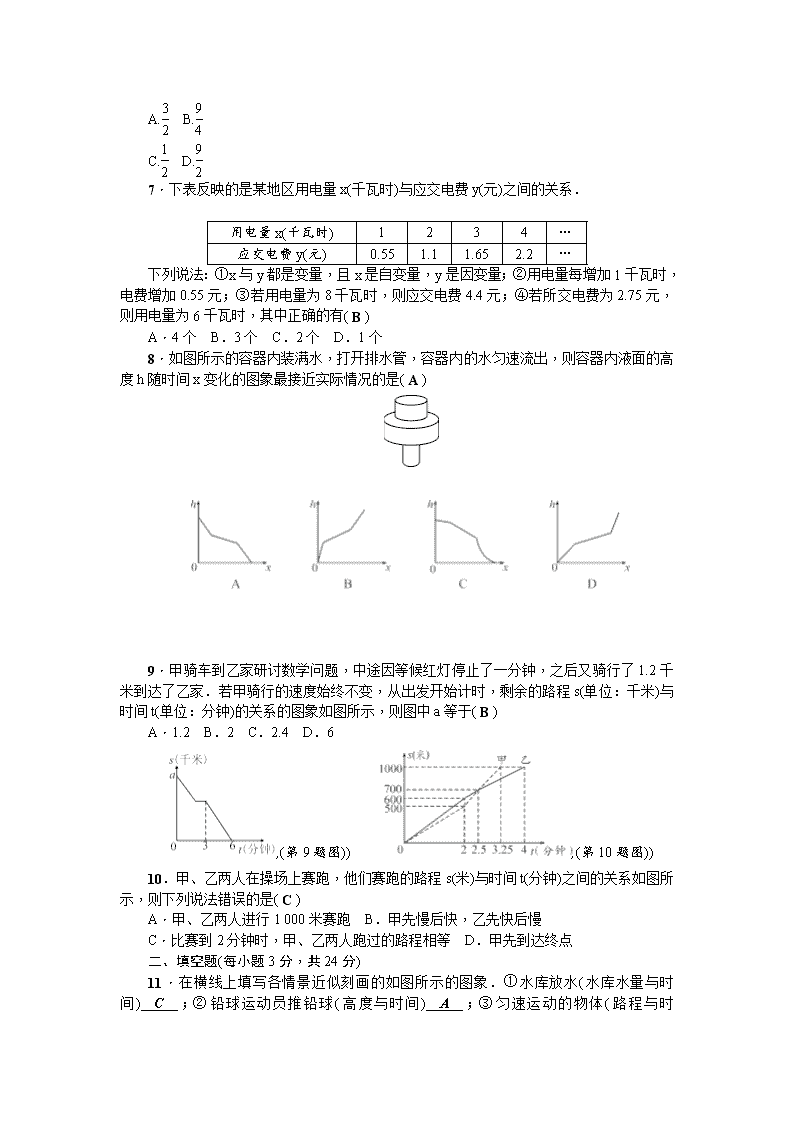
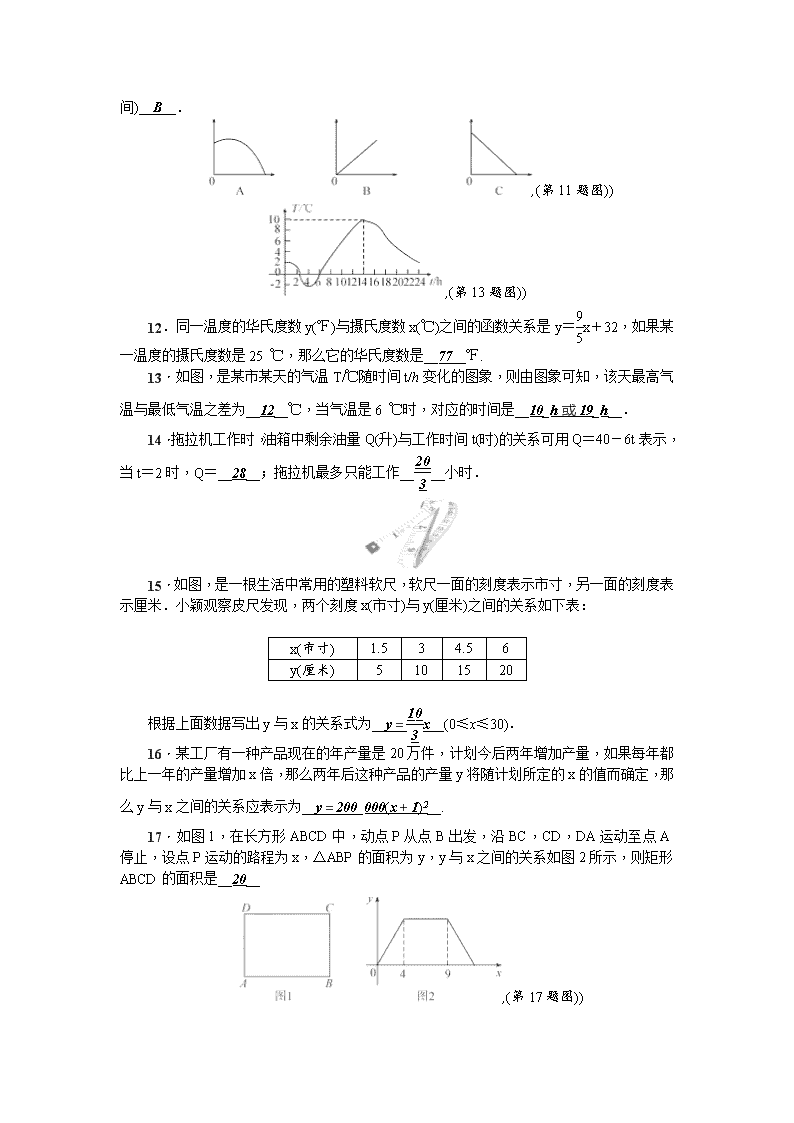
第三章检测题 时间：120 分钟 满分：120 分 一、选择题(每小题 3 分，共 30 分) 1．在球的体积公式 V＝4 3 πr3 中，下面说法正确的是( C ) A．V，π，r 是变量，4 3 是常量 B．V，r 是变量，4 3 是常量 C．V，r 是变量，4 3 ，π是常量 D．以上都不对 2．小明到某商店去购买钢笔，三次购买某型号的钢笔数量和所需的费用如下表所示， 根据表格说明这家商店此型号的钢笔的价格大致为( C )2 购买数量(支) 2 3 5 所需费用(元) 11.6 17.4 29 A.11.6 元/支 B．17.4 元/支 C．5.8 元/支 D．不能确定 3．长方形的周长为 60 cm，其中一条边为 x(其中 x＞0)，面积为 y cm2，则在这个长 方形中，y 与 x 的关系式可以写为( B ) A．y＝60x－2x2 B．y＝30x－x2 C．y＝x2－60 D．y＝x2－30 4．某次试验中，测得两个变量 v 和 m 的对应数据如下表，则 v 和 m 之间的关系最接近 下列关系式中的( D ) m 1 2 3 4 5 6 7 v 6.10 2.90 2.01 1.51 1.19 1.05 0.86 A.v＝m2－2 B．v＝6m C．v＝3m－1 D．v＝6 m 5．小明的父亲饭后出去散步，从家走 20 分钟到一个离家 900 米的报亭，看 10 分钟报 纸后，用 15 分钟返回家里．下面四个图象中，表示小明父亲的离家距离 y(米)与时间 x(分) 之间关系的是( B )【 6．如图，“机器图”输入 x 面临两个入口，依照机器中的对应关系，若输入的 x 的值为 3 2 ，则因变量 y 值为( C ) A.3 2 B.9 4 C.1 2 D.9 2 7．下表反映的是某地区用电量 x(千瓦时)与应交电费 y(元)之间的关系． 用电量 x(千瓦时) 1 2 3 4 … 应交电费 y(元) 0.55 1.1 1.65 2.2 … 下列说法：①x 与 y 都是变量，且 x 是自变量，y 是因变量；②用电量每增加 1 千瓦时， 电费增加 0.55 元；③若用电量为 8 千瓦时，则应交电费 4.4 元；④若所交电费为 2.75 元， 则用电量为 6 千瓦时，其中正确的有( B )2·1·c·n·j·y A．4 个 B．3 个 C．2 个 D．1 个 8．如图所示的容器内装满水，打开排水管，容器内的水匀速流出，则容器内液面的高 度 h 随时间 x 变化的图象最接近实际情况的是( A ) 9．甲骑车到乙家研讨数学问题，中途因等候红灯停止了一分钟，之后又骑行了 1.2 千 米到达了乙家．若甲骑行的速度始终不变，从出发开始计时，剩余的路程 s(单位：千米)与 时间 t(单位：分钟)的关系的图象如图所示，则图中 a 等于( B ) A．1.2 B．2 C．2.4 D．6 ,(第 9 题图)) ,(第 10 题图)) 10．甲、乙两人在操场上赛跑，他们赛跑的路程 s(米)与时间 t(分钟)之间的关系如图所 示，则下列说法错误的是( C )w A．甲、乙两人进行 1 000 米赛跑 B．甲先慢后快，乙先快后慢 C．比赛到 2 分钟时，甲、乙两人跑过的路程相等 D．甲先到达终点 二、填空题(每小题 3 分，共 24 分) 11．在横线上填写各情景近似刻画的如图所示的图象．①水库放水(水库水量与时 间)__C__；②铅球运动员推铅球(高度与时间)__A__；③匀速运动的物体(路程与时间)__B__． ,(第 11 题图)) ,(第 13 题图)) 12．同一温度的华氏度数 y(℉)与摄氏度数 x(℃)之间的函数关系是 y＝9 5x＋32，如果某 一温度的摄氏度数是 25 ℃，那么它的华氏度数是__77__℉.www-2-1-cnjy-com 13．如图，是某市某天的气温 T/℃随时间 t/h 变化的图象，则由图象可知，该天最高气 温与最低气温之差为__12__℃，当气温是 6 ℃时，对应的时间是__10_h 或 19_h__． 14．拖拉机工作时，油箱中剩余油量 Q(升)与工作时间 t(时)的关系可用 Q＝40－6t 表示， 当 t＝2 时，Q＝__28__；拖拉机最多只能工作__20 3 __小时． 15．如图，是一根生活中常用的塑料软尺，软尺一面的刻度表示市寸，另一面的刻度表 示厘米．小颖观察皮尺发现，两个刻度 x(市寸)与 y(厘米)之间的关系如下表： x(市寸) 1.5 3 4.5 6 y(厘米) 5 10 15 20 根据上面数据写出 y 与 x 的关系式为__y＝10 3 x__(0≤x≤30)． 16．某工厂有一种产品现在的年产量是 20 万件，计划今后两年增加产量，如果每年都 比上一年的产量增加 x 倍，那么两年后这种产品的产量 y 将随计划所定的 x 的值而确定，那 么 y 与 x 之间的关系应表示为__y＝200_000(x＋1)2__. 17．如图 1，在长方形 ABCD 中，动点 P 从点 B 出发，沿 BC，CD，DA 运动至点 A 停止，设点 P 运动的路程为 x，△ABP 的面积为 y，y 与 x 之间的关系如图 2 所示，则矩形 ABCD 的面积是__20__ ,(第 17 题图)) ,(第 18 题图)) 18．如图，折线 ABCDE 描述了一汽车在某一直线公路上的行驶过程中，汽车离出发地 的距离 s(千米)和行驶时间 t(小时)之间的关系，根据图中提供的信息，给出下列说法：①汽 车共行驶了 120 千米；②汽车在行驶途中停留了 0.5 小时；③汽车在整个行驶过程中的平均 速度为80 3 千米/时；④汽车自出发后 3 小时至 4.5 小时之间行驶的速度在逐渐减小．其中正确 的说法有__②__ 三、解答题(共 66 分) 19．(6 分)生物学研究表明，在 8～17 岁期间，男女生身高增长速度规律呈现如图所示， 请你观察此图，回答下列问题：男生身高增长速度的巅峰是几岁？在几岁时男生、女生的身 高增长速度是一样的？ 解：由男生图象最高点的横坐标看出，男生身高增长速度的巅峰是 13 岁；由图象的交 点看出，在 11 岁时男生、女生身高增长速度是一样的． 20．(9 分)小明从家给外地的姑妈打长途电话，按时收费，3 分钟内收费 1.8 元，每增加 1 分钟(不足 1 分钟按 1 分钟算)加收 0.39 元钱，小明和姑妈已通话 7 分钟． (1)上述过程中哪些量在发生变化？自变量和因变量各是什么？ (2)请完成通话计费表： 通话时间 前 3 分 4 分 5 分 6 分 7 分 … 收费 1.8 元 2.19 元 2.58 元 2.97 元 3.36 元 … (3)根据表格中的数据，粗略说明收费随时间变化而变化的 情况． 解： (1)通话时间与收费都在发生变化，其中通话时间是自变量，收费是因变量． (3)收费随时间的增加而增加． 21．(9 分)我们知道：海拔高度每上升 1 000 米，温度大约下降 6 ℃.现在在海拔 500 米 的某地温度为 15 ℃. (1)请计算在海拔 2 000 米高度的温度大约是多少摄氏度？ (2)用 x 表示海拔高度(米)，y 表示温度(℃)，请写出 y 与 x 之间的关系式； (3)利用(2)的结论计算海拔 3 000 米处的气温是多少摄氏度？ 解：(1)6 ℃.点拨：水平面的温度为 500 1 000 ×6＋15＝18(℃)，海拔 2 000 米高度的温度为 18－2 000 1 000 ×6＝6(℃) (2)y＝18－0.006x.(3)0 ℃. 22．(9 分)如图，向平静的水面投入一枚石子会在水面上激起一圈圈圆形涟漪，这些圆 的__圆心__相同． (1)由石子的入水点观察，由近及远，这些圆的面积如何变化？ (2)在这个变化过程中，自变量、因变量各是什么？ (3)如果圆的半径为 r，面积 S 可以表示为__S＝πr2__； (4)当半径 r 从 2 cm 变到 5 cm 时，圆的面积从__4π__cm2 变到__25π__cm2. 解：(1)逐渐增大． (2)圆的半径是自变量，圆的面积是因变量． 23．(10 分)某项研究表明，人在运动时的心跳速度通常与人的年龄有关，下表是测得一 个人在运动时所能承受的每分钟心跳的最高次数 y(次)随这个人的年龄 x(岁)变化的规律． 年龄 x(岁) 1 2 3 4 5 … 运动时所能承受的 心跳的最高次数 y(次/分) 175 174.2 173.4 172.6 171.8 … (1)求出 y 关于 x 的关系式； (2)正常情况下，在运动时，一个 12 岁的少年能承受的每分钟心跳的最高次数是多少次？ (3)一个 50 岁的人在运动时，每分钟心跳的次数为 148 次，问他有危险吗？ 解：(1)y＝175.8－0.8x. (2)166.2 次． (3)把 x＝50 代入 y＝175.8－0.8x 得 y＝135.8.因为 135.8<148，所以他有危险． 24．(11 分)一列快车、一列慢车同时从相距 300 km 的两地出发，相向而行．如图，分 别表示两车到目的地的距离 s(km)与行驶时间 t(h)的关系. (1)快车的速度为 __45__km/h，慢车的速度为 __30__km/h； (2)经过多久两车相遇？ (3)当快车到达目的地时，慢车距离目的地多远？ 解：(1)快车的速度为 300÷20 3 ＝45(km/h)，慢车的速度为 300÷10＝30(km/h), 故答案为： 45 30.2 (2) 300 45＋30＝4(h)．答：经过 4 h 两车相遇． (3)(10－20 3 )×30＝100(km)．答：当快车到达目的地时，慢车距离目的地 100 km. 25．(12 分)一水果个体户在批发市场按每千克 1.8 元批发了若干千克的西瓜在城镇出售， 为了方便，他带了一些零钱备用．他先按市场价售出一些后，又降价出售．售出西瓜千克数 x 与他手中持有的钱数 y 元(含备用零钱)的关系如图所示，结合图象回答下列问题： (1)水果个体户自带的零钱是多少？ (2)降价前他每千克西瓜出售的价格是多少？ (3)随后他按每千克下降 0.5 元将剩余的西瓜售完，这时他手中的钱(含备用的钱)是 450 元，问他一共批发了多少千克的西瓜？ 2-1-c-n-j-y (4)这位水果个体户一共赚了多少钱？ 解：(1)由图可得水果个体户自带的零钱为 50 元． (2)(330－50)÷80＝3.5(元)．答：降价前他每千克西瓜出售的价格是 3.5 元． (3)(450－330)÷(3.5－0.5)＝40(千克), 80＋40＝120(千克)．答：他一共批发了 120 千克的 西瓜 (4)450－120×1.8－50＝184(元)．答：这个水果个体户一共赚了 184 元钱．