- 2021-05-08 发布 |
- 37.5 KB |
- 30页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版八年级下册数学同步练习课件-第6章-1 平行四边形的性质(二)
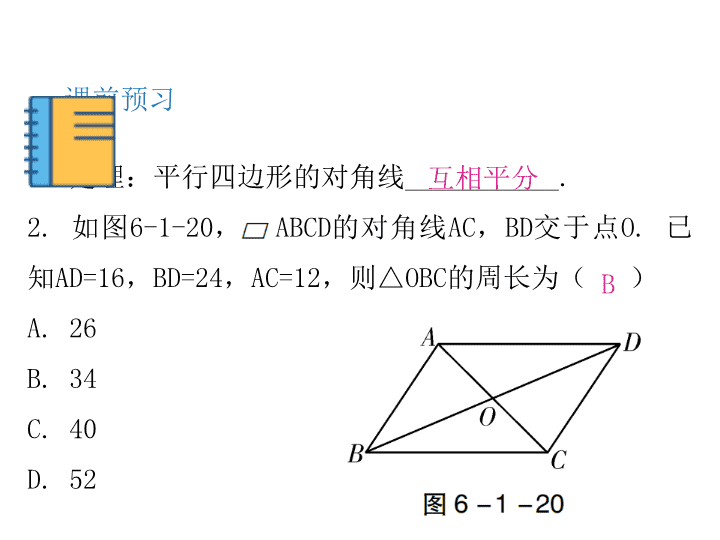
中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品 学资源 中小学精品教学 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中 学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中 精品教学资源 中小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品 学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中 学精品教学资源 中 精品教学资源 中小学精品教学资源 中小 品教学 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 精 品 教 学 资 源 中小学精品教 资源 中 小 学 精 品 教 学 资 源中小学精品教 资源 中 小 学 精 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 学 精 品 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精 教学资中小学精品教学资 中小学精品教学资源 中小学精品教学资源 中小 精品教学资源 中小学 品教学资源 中小 精品教学资源 中小 精品教 资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学 源 中 小 学 精 品 教 学 资 源 中小学精品 资源 中小学精品教学 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 小学精品教 资源 中小学精品教 资源中小学精品教学资源 学精品教学资源 中 学精 教学资源 中 小 学 精 品 教 学 资 源 中 学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学 品教学资源中 精品教学资源 小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中 学精品教学资 中小 精品教学资源 中小学精品教学资源 中小学精品 中小 精品教 资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小 精品 学资源 中 小 学 精 品 教 学 资 源 中小 精品 学资源 中 学精品教 资源中小 精品教学资源 中小学精品教学资源 中 学精品 资源 中 教学资源 中 精 教学资源 中小 品教学 源 中 小 学 精 品 教 学 资 源 小 学 精 品 教 学 资 源 中 小 学 品 教 资 源 中 小 学 品 教 资 源 中 小 品 教 资 源小学精品教 资 中 小 学 精 品 教 学 资 源中小学精品教 资 中 小 学 精 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 学 精 品 教 学 资 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 学 精 品 教 资 源 中 小 学 品 学 资 源 中 小 学 精 品 教 学 资 源 中 小 精 品 教 学 资 源 中小学精品教学资源 中小 精 教中小学精品教学 中小学精品教学资源 中小学 品教学资 中小 精品教学资源 中小 品教学资源 精品教学资源 1 平行四边形的性质 第六章 平行四边形 第2课时 平行四边形的性质 (二) 课前预习 1. 定理:平行四边形的对角线___________. 2. 如图6-1-20, ABCD的对角线AC,BD交于点O. 已 知AD=16,BD=24,AC=12,则△OBC的周长为( ) A. 26 B. 34 C. 40 D. 52 互相平分 B 3. 如图6-1-21, ABCD的对角线AC与BD相交于点O, AC⊥BC,且AB=10,AD=6,则OB的长度为( ) A.2 B.4 C.8 D.4 4. 如图6-1-22,在 ABCD中,AB=3 cm,BC=5 cm, 对角线A C, B D相交于点O,则O A的取值范围是 ____________. 1<OA<4 A 课堂讲练 典型例题 新知:平行四边形的性质——平行四边形的对角线互 相平分 【例1】如图6-1-23,在 ABCD中,O是对角线AC,BD 的交点,下列结论错误的是( ) A. AB∥CD B. AB=CD C. AC=BD D. OA=OC C 模拟演练 1. 如图6-1-24, ABCD的对角线AC,BD相交于点O, 则下列说法一定正确的是( ) A. AO=OD B. AO⊥OD C. AO=OC D. AO⊥AB C 【例2】如图6-1-25, ABCD的周长为40,△BOC的周 长比△AOB的周长多10,则AB的长为( ) A. 20 B. 15 C. 10 D. 5 D 典型例题 2. 如图6-1-26, ABCD的对角线AC,BD相交于点O,且 AC+BD=16,CD=6,则△ABO的周长是( ) A. 10 B. 14 C. 20 D. 22 B 模拟演练 【例3】如图6-1-27, ABCD的对角线AC,BD相交于点O, EF过点O且与AB,CD分别相交于点E,F,连接EC. (1)求证:OF=OE; (2)若EF⊥AC,△BEC的周长 是10,求 ABCD的周长. 典型例题 (1)证明:∵四边形ABCD是平行四边形, ∴OD=OB,DC∥AB. ∴∠FDO=∠EBO. ∠FDO=∠EBO, 在△DFO和△BEO中,OD=OB, ∠FOD=∠EOB, ∴△DFO≌△BEO(ASA). ∴OF=OE. (2)解:∵四边形ABCD是平行四边形, ∴AB=CD,AD=BC,OA=OC. ∵EF⊥AC, ∴AE=CE. ∵△BEC的周长是10, ∴BC+BE+CE=BC+BE+AE=BC+AB=10. ∴ ABCD的周长=2(BC+AB)=20. 模拟演练 3. 如图6-1-28,在 ABCD中,对角线AC与BD相交于 点O,过点O作一条直线分别交AB,CD于点E,F. (1)求证:OE=OF; (2)若AB=6,BC=5,OE=2,求四边形BCFE的周长. (1)证明:在 ABCD中, ∵AC与BD相交于点O, ∴OA=OC,AB∥CD. ∴∠OAE=∠OCF. ∠OAE=∠OCF, 在△OAE和△OCF中,OA=OC, ∠AOE=∠COF, ∴△OAE≌△OCF(ASA). ∴OE=OF. (2)解:∵△OAE≌△OCF, ∴AE=CF. ∴BE+CF=AB=6. 又∵EF=2OE=4, ∴四边形BCFE的周长=BE+BC+CF+EF=6+4+5=15. 分层训练 A 组 1. 如图6-1-29, ABCD的对角线AC与BD相交于点O, AB⊥AC. 若AB=4,AC=6,则BD的长是( ) A. 8 B. 9 C. 10 D. 11 C 2. 如图6-1-30, ABCD中,下列说法一定正确的是 ( ) A.AC=BD B.AC⊥BD C.AO=CO D.AB=BC C 3. 如图6-1-31,在 ABCD中,O是AC,BD的交点,过 点O作AC的垂线交边AD于点E,连接CE.若 ABCD 的周 长为20 cm,则△CDE的周长为( ) A.6 cm B.8 cm C.10 cm D.12 cm C 4. 平行四边形的两条对角线分别为6和10,则其中一条 边x的取值范围为( ) A. 4<x<6 B. 2<x<8 C. 0<x<10 D. 0<x<6 5. 如图6-1-32,在 ABCD中,对角线AC,BD相交于点 O,过点O的直线分别交AD,BC于点M,N. 若△CON的面积 为2,△DOM的面积为4,则 ABCD 的面积为______. B 24 6. 如图6-1-33,在 ABCD中,AB=6,∠BAD=60°, ∠ABD=90°,对角线AC,BD交于点O,E为AD上一点,连 接EO.若△EDO的周长比四边形ABOE的周长大3,则ED的 长为________. B 组 7. 如图6-1-34,在平行四边形ABCD中,对角线AC,BD 相交于点O.过点O作EO⊥AC,交BC于点E,连接AE.已 知△ABE的周长为18,则对角线AC的最大整数值是 ______.17 8. 如图6-1-35,在 ABCD中,AB=5,AC=4,AD=3. (1)求 ABCD的面积; (2)求BD的长. 解:(1)∵四边形ABCD 是平行四边形, ∴CD=AB=5. ∵CD=5,AC=4,AD=3, ∴AD2+AC2=CD2. ∴∠DAC=90°,即AD⊥AC. ∴S ABCD=AD·AC=3×4=12. (2)∵四边形ABCD是平行四边形, ∴OA= AC=2. ∵∠DAC=90°, ∴OD= ∵四边形ABCD是平行四边形, ∴BD=2OD=2 . 9. 已知:如图6-1-36,AC,BD是 ABCD的两条对角线, AE⊥BD,CF⊥BD,垂足分别为点E,F.求证:OE=OF. 证明:∵四边形ABCD是平行四边形, ∴AB=CD,AB∥CD. ∴∠ABE=∠CDF. ∵AE⊥BD,CF⊥BD, ∴∠AEB=∠CFD=90°. 在△ABE和△CDF中, ∠AEB=∠CFD, ∠ABE=∠CDF, AB=CD, ∴△ABE≌△CDF(AAS). ∴BE=DF. ∵OB=OD,∴OB-BE=OD-DF,即OE=OF. C 组 10. 如图6-1-37,在 ABCD中,对角线AC,BD交于 点O,EO⊥AC. (1)若△ABE的周长为10 cm,求 ABCD的周长; (2)若∠ABC=78°,AE平分∠BAC,试求∠DAC的度数. 解:(1)∵四边形 ABCD 是平行四边形, ∴OA=OC. ∵OE⊥AC, ∴AE=CE. 故△ABE的周长=AB+BE+AE=AB+BC=10(cm). 根据平行四边形的对边相等,得 ABCD的周长为2×10=20(cm). (2)∵AE=CE,∴∠EAC=∠ECA. ∵∠ABC=78°,AE平分∠BAC, ∴∠BAE=∠EAC=∠ECA. ∴3∠ACE+78°=180°.∴∠ACE=34°. ∵AD∥BC,∴∠DAC=∠ACE=34°. 11. 如图6-1-38,在 ABCD中,点E是BC边的中点, 连接AE并延长与DC的延长线交于点F. (1)求证:CF=CD; (2)若AF平分∠BAD,连接DE,试判断DE与AF的位置 关系,并说明理由. (1)证明:∵四边形ABCD是平行四边形, ∴AB∥CD,AB=CD. ∵点F为DC的延长线上的一点, ∴AB∥DF. ∴∠BAE=∠CFE,∠ECF=∠EBA. ∵E为BC的中点,∴BE=CE. ∠BAE=∠CFE, 在△BAE和△CFE中, ∠EBA=∠ECF, BE=CE, ∴△BAE≌△CFE(AAS). ∴BA=CF. ∴CF=CD. (2)解:DE⊥AF. 理由如下: ∵AF平分∠BAD,∴∠BAF=∠DAF. ∵∠BAF=∠DFA,∴∠DAF=∠DFA. ∴DA=DF. 又由(1)知△BAE≌△CFE, ∴AE=EF. ∴DE⊥AF.查看更多