2014年1月黄埔中考数学一模试题

2014年1月黄埔中考数学一模试题

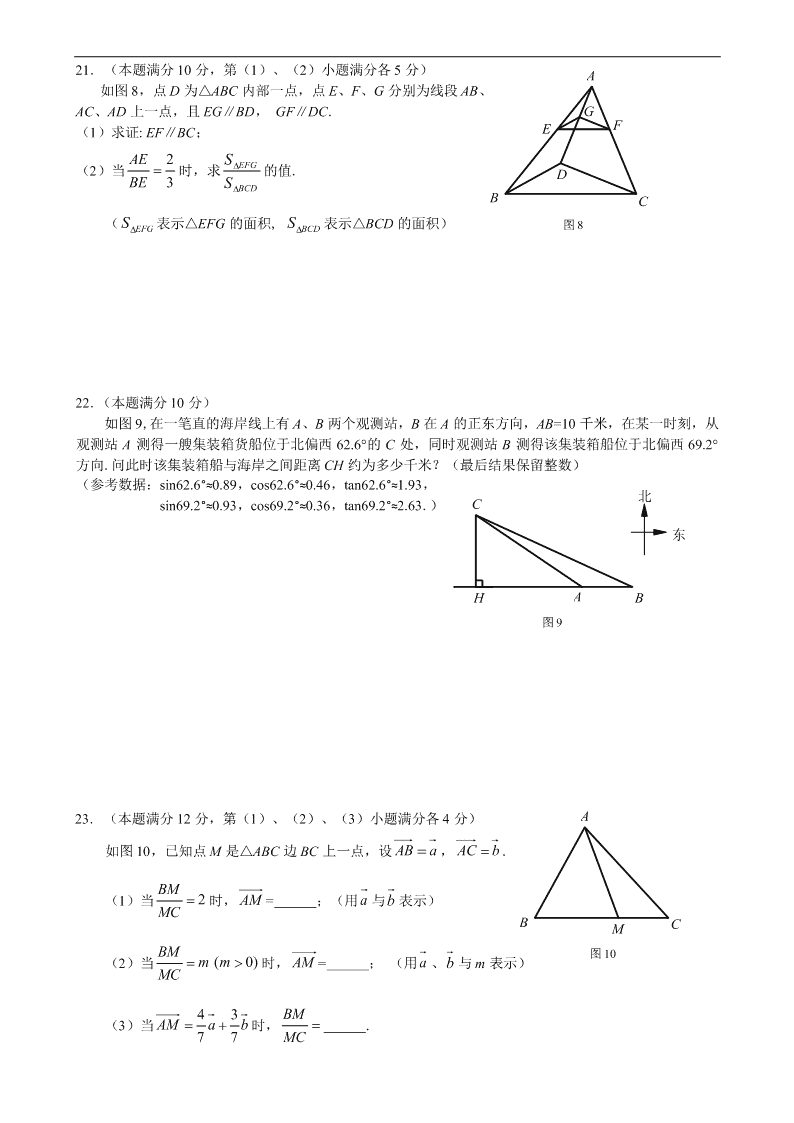
黄浦区 2013 学年度第一学期九年级期终调研测试 数 学 试 卷 （满分 150 分，考试时间 100 分钟） 考生注意： 1. 本试卷含三个大题，共 25 题； 2. 答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效； 3. 除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题：（本大题共 6 题，每题 4 分，满分 24 分） 【下列各题的四个选项中，有且只有一个是正确的，选择正确项的代号并填涂在答题纸的相应位置上.】 1. 抛物线 2 34y x x   的对称轴是（ ） A.直线 3x  ； B.直线 3x  ； C.直线 3 2x  ； D.直线 3 2x  ． 2. 抛物线 2y ax ( 0)a  的图像一定经过（ ） A.第一、二象限； B. 第三、四象限； C. 第一、三象限； D. 第二、四象限． 3. 如图 1，在平行四边形 ABCD 中，若 E 为 CD 中点，且 AE 与 BD 交于点 F，则△ EDF 与△ ABF 的周长 比为（ ） A. 1: 2 ； B. 1: 4 ； C. 1:3 ； D. 1:9 ． 4.如图 2，传送带和地面所成斜坡的坡度为 1:3，若它把物体从地面点 A 处送到离地面 2 米高 的 B 处， 则物体从 A 到 B 所经过的路程为（ ） A. 6 米； B. 10 米； C. 2 10 米； D. 3 10 米. 5. 在△ABC 中，D、E 分别是边 AB、AC 上的点，下列条件中不能．．判定△AED∽△ABC 是（ ） A. ∠ADE=∠C； B.∠AED=∠B； C. AD AC AE AB  ； D. AD AC BC DE ． 6.如图 3，在△ABC 中，∠ACB=90 ，CD 为边 AB 上的高，若 AB=1，则线段 BD 的长是（ ） A.sin2A； B.cos2A； C. tan2A； D. cot2A． 图1 F A ED B C 2米 传送带 图3 B A 图3 D C A B 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） 【请将结果直接填入答题纸的相应位置上】 7.如果线段 b 是线段 a、c 的比例中项，且 9a  ， 4c  ，那么b  . 8.计算：    32a b a b   = . 9.如图 4，AB∥CD∥EF，如果 : 2:3AC CE  ， 10BF  ，那么线段 DF 的长为 . 10.若将抛物线 2yx 向下平移 2 个单位，则所得抛物线的表达式是 . 11.如果抛物线 2( 2) 3y a x ax    的开口向上，那么 a 的取值范围是 . 12.若抛物线 2( ) 1y x m m    的对称轴是直线 1x  ，则它的顶点坐标是 . 13.若 AD、BE 是△ABC 的中线，AD、BE 相交于点 F，FD =2，则线段 AD 的长为 . 14.在△ABC 中，∠A = 90°，若 BC=4，AC=3，则 cos B = . 15.如图 5，在△ABC 中，若 AB=AC=3，D 是边 AC 上一点，且 BD=BC=2，则线段 AD 的长为 . 16.如图 6，在△ABC 中，AD 是 BC 上的高，且 BC= 5，AD =3，矩形 EFGH 的顶点 F、G 在边 BC 上，顶 点 E、H 分别在边 AB 和 AC 上，如果设边 EF 的长为 (0 3)xx ，矩形 EFGH 的面积为 y ，那么 y 关于 x 的函数解析式是 . 17.若抛物线    21 1 1y a x a x     与 x 轴有且仅有一个公共点，则 a 的值为 . 18.如图 7，在 Rt△ABC 中，∠C=90°，AC=3，cot 3 4A  ，点 D、E 分别是边 BC、AC 上的点，且∠EDC= ∠A，将△ABC 沿 DE 对折，若点 C 恰好落在边 AB 上，则 DE 的长为 . 三、解答题：（本大题共 7 题，满分 78 分） 19.（本题满分 10 分） 计算： 2sin30 tan 60 2cos30 cot 45       . 20.（本题满分 10 分，第（1）小题满分 7 分，第（2）小题满分 3 分） 已知：抛物线 2y ax b x c   经过 A（-1，8）、B（3，0）、C（0，3）三点． （1）求抛物线的表达式； （2）写出该抛物线的顶点坐标． E D CB A 图 7 E D A B CF G H 图 6 D CB A 图 5 图 4 F D B E C A 21. （本题满分 10 分，第（1）、（2）小题满分各 5 分） 如图 8，点 D 为△ABC 内部一点，点 E、F、G 分别为线段 AB、 AC、AD 上一点，且 EG∥BD， GF∥DC. （1）求证: EF∥BC； （2）当 2 3 AE BE  时，求 EFG BCD S S   的值. （ EFGS 表示△EFG 的面积, BCDS 表示△BCD 的面积） 22.（本题满分 10 分） 如图 9,在一笔直的海岸线上有 A、B 两个观测站，B 在 A 的正东方向，AB=10 千米，在某一时刻，从 观测站 A 测得一艘集装箱货船位于北偏西 62.6°的 C 处，同时观测站 B 测得该集装箱船位于北偏西 69.2° 方向.问此时该集装箱船与海岸之间距离 CH 约为多少千米？（最后结果保留整数） （参考数据：sin62.6°≈0.89，cos62.6°≈0.46，tan62.6°≈1.93， sin69.2°≈0.93，cos69.2°≈0.36，tan69.2°≈2.63.） 23. （本题满分 12 分，第（1）、（2）、（3）小题满分各 4 分） 如图 10，已知点 M 是△ABC 边 BC 上一点，设 AB a ， AC b . （1）当 2BM MC  时， AM = ；（用 a 与b 表示） （2）当 ( 0)BM mm MC 时， = ； （用 、 与 m 表示） （3）当 43 77 AM a b时， BM MC  . F G A B D C E 图 8 北 东 图 9 H A B C A B CM 图 10 24.（本题满分 12 分，第（1）、（2）、（3）小题满分各 4 分） 如图 11，在平面直角坐标系 xOy 中，顶点为 M 的抛物线是由抛物线 2 3yx向右平移一个单位后 得到的，它与 y 轴负半轴交于点 A，点 B 在该抛物线上，且横坐标为 3． （1）求点 M、A、B 坐标； （2）联结 AB、AM、BM ，求 ABM 的正切值； （3）点 P 是顶点为 M 的抛物线上一点，且位于对称轴的右侧，设 PO 与 x 正半轴的夹角为 ，当 ABM  时，求 P 点坐标． 25.（本题满分 14 分，第（1）小题满分 4 分，第（2）、（3）小题满分各 5 分） 如图 12，在△ABC 中，∠ACB=90°，AC=8，sin 4 5B  ，D 为边 AC 中点，P 为边 AB 上一点 (点 P 不与 点 A、B 重合) ，直线 PD 交 BC 延长线于点 E，设线段 BP 长为 x ，线段 CE 长为 y . （1）求 y 关于 的函数解析式并写出定义域； （2）过点 D 作 BC 平行线交 AB 于点 F，在 DF 延长线上取一点 Q，使得 QF=DF， 联结 PQ、QE，QE 交边 AC 于点 G， ①当△EDQ 与△EGD 相似时，求 的值； ②求证： PD DE PQ QE  . B M A x y O 图 11 E D CB A P 图 12 黄浦区 2013 学年度第一学期九年级期终调研测试数学参考答案与评分标准 一、选择题：（本大题共 6 题，每题 4 分，满分 24 分） 1. D； 2. B； 3. A ； 4. C ； 5. D ； 6. A. 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） 7. 6 ； 8. 5ab ； 9. 6； 10. 22  xy ； 11. 2a  ； 12.(1, 2) ； 13. 6； 14. 7 4 ； 15. 5 3 ； 16. 2 55 3yxx   ； 17. 3； 18. 125 48 . 三、解答题：（本大题共 7 题，满分 78 分） 19.解：原式= 1232 3212   ……………………………………………………（8 分） = 2( 3 1) ( 3 1)( 3 1)   …………………………………………（1 分） = 23 . ………………………………………………………（1 分） 20.解：（1）由抛物线 2y ax b x c   经过 C（0，3）可知 3c  . …………（2 分） 由抛物线 2 3y ax b x   经过 A（-1，8）、B（3，0）得 2 2 ( 1) ( 1) 3 8, 3 3 3 0. ab ab               ………………………………………………………（2 分） 解得 1, 4. a b    …………………………………………………………（2 分） ∴该抛物线的表达式为 2 43y x x   . ………………………………………（1 分） （2）由 配方得 2( 2) 1yx   . …………………………………（2 分） ∴顶点坐标为（2，-1）. ………………………………………………… （1 分） 21.解：（1）∵EG∥BD，∴ AE AG EB GD  . …………………………………………（1 分） ∵GF∥DC，∴ AG AF GD FC  . ………………………………………………………（1 分） ∴ AE AF EB FC  . …………………………………………………………………（1 分） ∴EF∥BC. …………………………………………………………………（2 分） （2）∵EF∥BC，∴ AEF ABC   . ∵EG∥BD，∴ AEG ABD   . ∴ AEF AEG ABC ABD     ， 即 GEF DBC   . ………………………………………………………………（1 分） 同理 GFE DCB   . …………………………………………………………（1 分） ∴△ EGF ∽△ BDC . …………………………………………………………（1 分） ∵ 2 3 AE BE  ，∴ 2 5 EF BC  . ……………………………………………………（1 分） ∴ EFG BCD S S   = 2 25 4()EF BC  . ………………………………………………………（1 分） 22.解：设 CH=x. 在 Rt△AHC 中， 62.6ACH . ………………………………（1 分） ∵ tan AHACH CH ，∴ tan 62.6AH x . …………………………………………（2 分） 在 Rt△BHC 中， 69.2BCH . ………………………………………………（1 分） ∵ tan BHBCH CH .∴ tan 69.2BH x . …………………………………………（2 分） ∵ AB BH AH, ∴ tan 69.2 tan 62.6 10xx. ……………………………（2 分） 解得 tan 69.2 tan 62.6 10 xx x   ≈14. ………………………………………………（2 分） 答：此时该集装箱船与观测站 A 的距离约为 14 千米. 23.解：（1） 12 33a b ； （2） 1 11a m bmm ； （3） 3 4 . (每空 4 分) 24. 解：（1）解析式为 2( 1) 3yx   ， 顶点坐标为 M（1， 3 ）. ………（2 分） A（0， 2 ）， B（3，1）. …………………………………………（2 分） （2）过点 B、M 分别作 BE⊥AO，MF⊥AO，垂足分别为 E、F. ∵EB=EA=3，∴∠EAB=∠EBA=45°. 同理∠FAM=∠FMA=45°. ∴△FAM ∽ △EAB. ∴ 1 3 AM AB AE AF  . ∵∠EAB=∠FAM=45°∴∠BAM=90°. ………………………………………（2 分） ∴Rt△ABM 中， 1tan 3 AMABM BM    . ………………………………………………（2 分） （3）过点 P 作 PH⊥ x 轴，垂足为 H. 设点 P 坐标为 2( , 2 2)x x x. ……………………………………………………………（1 分） 1°当点 P 在 轴上方时， 由题意得 2 2 3 2 1xx x  ，解得 1 2 3 x  （舍）， 2 3x  . ∴点 P 坐标为(3,1) . ……………………………………………………………（1 分） 2°当点 P 在 轴下方时， 题意得 2 221 3 xx x  ，解得 1 5 97 6 x  （舍）， 2 5 97 6 x  . ∴点 P 坐标为(,5 )97 5 97 6 18. …………………………………………………（1 分） 综上所述，P 点坐标为 ， . ………………………………（1 分） 25. 解：（1）在 Rt△ACB 中， 8AC  ， 6BC  ， 10AB  . ……………………（1 分） 过点 P 作 PH⊥BE，垂足为 H. ………………………………………………（1 分） 在 Rt△PHB 中， 4 5 PH x ， 3 5 BH x . ∵CD∥HP，∴ CE CD PHEH  ，即 4 346 55 y y x x   . 解得 30 3 5 xy x   (5 10x ). ……………………………………………… （2 分） （2）联结 QB，∵DQ=BC=6，DQ∥BC， ∴四边形 QBCD 是平行四边形. ∴BQ=4. 又∵∠ACB=90°，∴∠EBQ =90°. ………………………………… ………………（1 分） 当△EDQ 与△EGD 相似时，∵∠EDG <∠EDQ∴∠EDC =∠DQE. ∵DQ∥CE，∴∠DQE =∠QEB，∴∠EDC =∠QEB . 又∵∠EBQ=∠DCE=90°∴△EBQ ∽△DCE . …………………………………（2 分） ∴ CE CD BQ BE ，即 4 46 y y  ，解得 1 8y  （舍） 2 2y  . ………………………（1 分） 代入 30 3 5 xy x   ， 得 8x  . …………………………………………………………（1 分） （3）延长 PQ，交 EB 延长线于 M. …………（1 分） ∵DQ∥ME，∴ QF PF FD MB PB BE . 又∵QF FD ，∴MB=BE. …………………（1 分） M G Q E F D CB A P 又由①得 QB⊥ME, …………………（1 分） ∴QE=QM. …………………………………（1 分） ∵DQ∥ME，∴ PD PQ DE QM  . 又∵QE=QM，∴ PD PQ DE QE  .即 PD DE PQ QE  . …………………………………………（1 分）