- 2021-05-07 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019-2020学年福建省长汀、连城一中等六校高一上学期期中考联考试题 数学
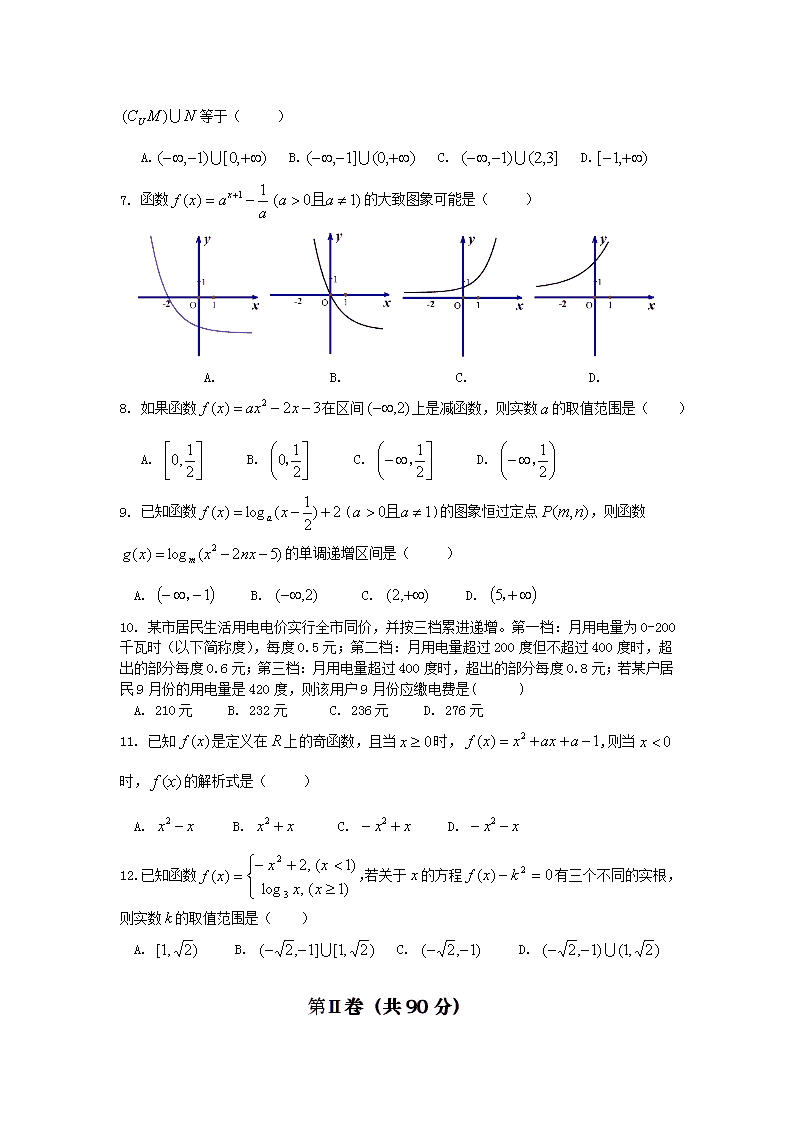
“长汀、连城、上杭、武平、永定、漳平”六县(市/区) 一中联考 2019-2020学年第一学期半期考 高一数学试题 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟. 注意事项:1.考生将自己的姓名、准考证号及所有的答案均填写在答题卡上. 2.答题要求见答题卡上的“填涂样例”和“注意事项”. 第Ⅰ卷(选择题共60分) 一.选择题(共12小题,每小题5分,共60分。在每小题列出的四个选项中,只有一项符合要求) 1. 已知集合,则与集合的关系是( ) A. B. C. D. 2. 函数的定义域是( ) A. B. C. D. 3. 下列函数中是偶函数但不是奇函数的是( ) A. B. C. D. 4. 已知,则下列关系式正确的是( ) A. B. C. D. 5. 函数的零点所在的区间是( ) A. (-2,-1) B. (-1,0) C. (0,1) D. (1,2) 6. 已知全集,集合,集合,则 等于( ) A. B. C. D. 7. 函数的大致图象可能是( ) A. B. C. D. 8. 如果函数在区间上是减函数,则实数的取值范围是( ) A. B. C. D. 9. 已知函数()的图象恒过定点,则函数的单调递增区间是( ) A. B. C. D. 10. 某市居民生活用电电价实行全市同价,并按三档累进递增。第一档:月用电量为0-200千瓦时(以下简称度),每度0.5元;第二档:月用电量超过200度但不超过400度时,超出的部分每度0.6元;第三档:月用电量超过400度时,超出的部分每度0.8元;若某户居民9月份的用电量是420度,则该用户9月份应缴电费是( ) A. 210元 B. 232元 C. 236元 D. 276元 11. 已知是定义在上的奇函数,且当时,,则当时,的解析式是( ) A. B. C. D. 12.已知函数,若关于的方程有三个不同的实根,则实数的取值范围是( ) A. B. C. D. 第Ⅱ卷(共90分) 二.填空题(本题共4个小题,每小题5分,共20分) 13. 已知函数,则的值为__________. 14. 已知定义在上的偶函数在区间上是减函数,若,则实数的取值范围是__________. 15. 若函数的值域为,则为__________. 16.已知函数为偶函数,且,若不相等的两正数满足,则不等式的解集为__________. 三.解答题(本题共6小题,共70分.要求写出必要的文字说明和解题过程.) 17.(本题满分10分)求值与化简 (1) (2) 18.(本题满分12分) 设集合,, (1)全集,求; (2)若,求实数的取值范围. 19.(本题满分12分)已知函数为奇函数,且. (1)求实数的值; (2)判断在区间上的单调性,并用定义证明你的结论; (3) 求不等式的解集. 20.(本题满分12分)某机械制造厂生产一种新型产品,生产的固定成本为20000元,每生产一件产品需增加投入成本100元。根据初步测算,当月产量是件时,总收益(单位:元)为 ,利润=总收益-总成本. (1)试求利润(单位:元)与(单位:件)的函数关系式; (2)当月产量为多少件时利润最大?最大利润是多少? 21.(本题满分12分)设为非负实数,函数. (1)当时,画出函数的草图,并写出函数的单调递增区间; (2)若函数有且只有一个零点,求实数的取值范围. 22.(本题满分12分)已知函数. (1)求在区间的值域; (2)函数,若对于任意,总存在,使得恒成立,求实数的取值范围. 参考答案 一.选择题(每题5分)1--12 ABCBB AAADC CD 二.填空题(每题5分)13. 9 14. 15. 16. 三.解答题 17.解:(1)原式=..........5分 (2)原式=.......10分 18.解:(1) ..........2分 ...................4分 (2) ∵ ∴.................6分 当时,..................8分 当时,依题意得,解得..........10分 综上所述,的取值范围是................12分 19.解:(1)由题意,为R上奇函数,则,得,再由,得。经检验,当,时是奇函数。.................3分 (2) 由(1)得,在上单调递减。.................4分 证明如下: 任取且,则 ,∴,,∴,即 ∴在上单调递减..............8分 (3)∵为奇函数,∴,则原不等式化为 ,而由(2)得在时单调递减,且 ∴,即,∴ ∴原不等式的解集为..............12分 20.解:(1)依题意, 当时............2分 当时..............4分 ∴...............6分 (2)当时,∴当....8分 当时,..............10分 ∴当............12分 21.解:(1)函数的草图如右. ....................4分 由图可知函数的增区间为................6分 (2) 因为,而则。 若时有唯一零点。符合题意................8分 若时在上单调递增,,∴在上有唯一零点。而在上单调递增,在上单调递减。由题意,要使在R上有唯一零点,则在上没有零点,故在上的最大值 ,∴. 综合上述,的取值范围是...............12分 22.解:(1)易知在[0,1]上单调递增,∴ ∴值域为...........4分 (2)设, ,易知............6分 令,则 ∵在上递减,在上递增. ∴.即............9分 由题意知,,即,∴.............12分查看更多