- 2021-05-07 发布 |
- 37.5 KB |
- 12页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【精品试卷】中考数学一轮复习 专题测试17 三角形与多边形(培优提高)(教师版)
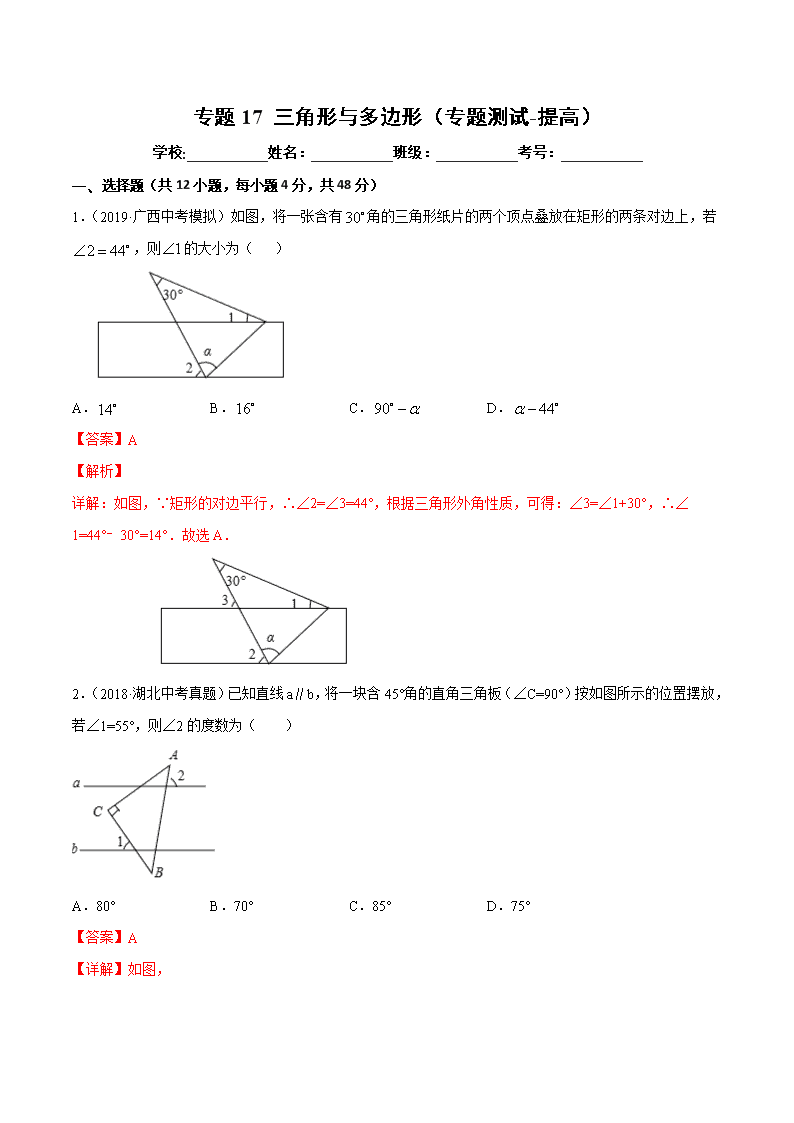
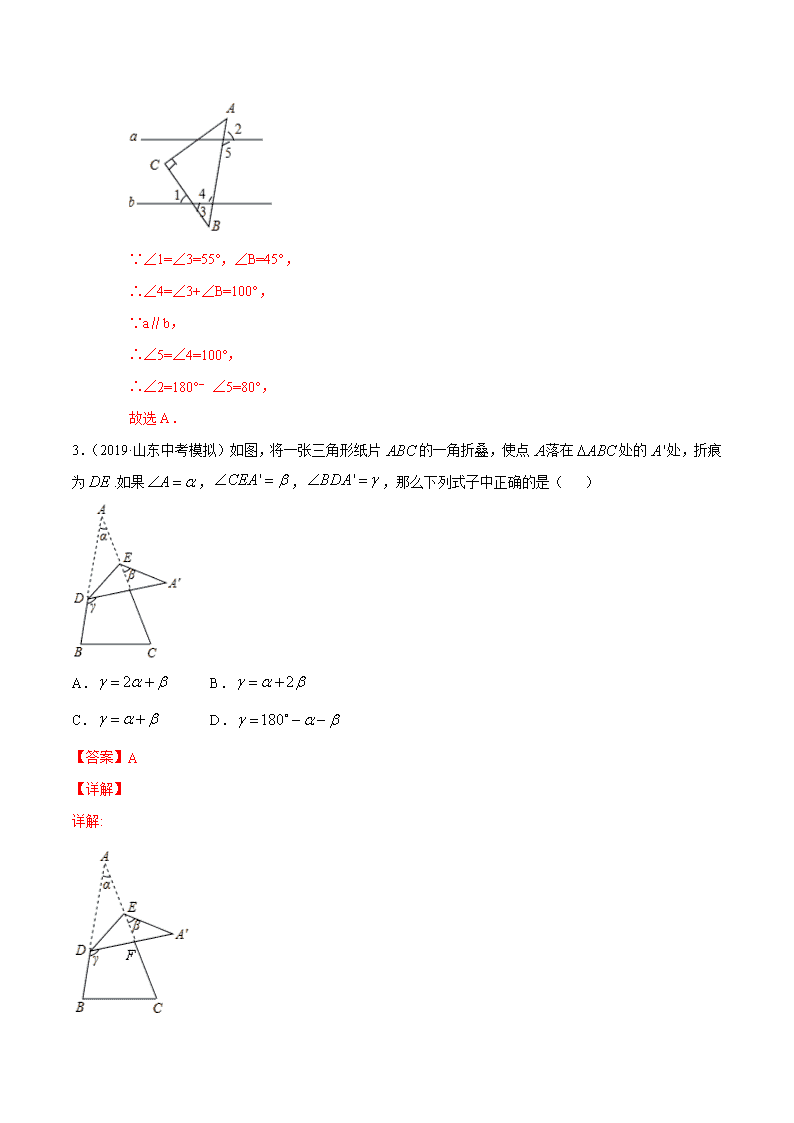
专题 17 三角形与多边形(专题测试-提高) 学校:___________姓名:___________班级:___________考号:___________ 一、选择题(共 12 小题,每小题 4 分,共 48 分) 1.(2019·广西中考模拟)如图,将一张含有30 角的三角形纸片的两个顶点叠放在矩形的两条对边上,若 2 44 ,则 1 的大小为( ) A.14 B.16 C.90 D. 44 【答案】A 【解析】 详解:如图,∵矩形的对边平行,∴∠2=∠3=44°,根据三角形外角性质,可得:∠3=∠1+30°,∴∠1=44° ﹣30°=14°.故选 A. 2.(2018·湖北中考真题)已知直线 a∥b,将一块含 45°角的直角三角板(∠C=90°)按如图所示的位置摆放, 若∠1=55°,则∠2 的度数为( ) A.80° B.70° C.85° D.75° 【答案】A 【详解】如图, ∵∠1=∠3=55°,∠B=45°, ∴∠4=∠3+∠B=100°, ∵a∥b, ∴∠5=∠4=100°, ∴∠2=180°﹣∠5=80°, 故选 A. 3.(2019·山东中考模拟)如图,将一张三角形纸片 ABC 的一角折叠,使点 A 落在 ABC 处的 'A 处,折痕 为 DE .如果 A , 'CEA , 'BDA ,那么下列式子中正确的是( ) A. 2 B. 2 C. D. 180 【答案】A 【详解】 详解: 由折叠得:∠A=∠A', ∵∠BDA'=∠A+∠AFD,∠AFD=∠A'+∠CEA', ∵∠A=α,∠CEA′=β,∠BDA'=γ, ∴∠BDA'=γ=α+α+β=2α+β, 故选 A. 4.(2018·云南中考真题)若一个正多边形的内角和为 720°,则这个正多边形的每一个内角是( ) A.60° B.90° C.108° D.120° 【答案】D 【详解】 (n-2)×180°=720°, ∴n-2=4, ∴n=6. 则这个正多边形的每一个内角为 720°÷6=120°. 故选 D. 5.(2018·广西中考模拟)一个多边形少加了一个内角时,它的度数和是 1310°,则这个内角的度数为( ) A.120° B.130° C.140° D.150° 【答案】B 详解:设多边形的边数为 n,这个内角的度数为 x. ∵0<(n−2)180°−1310<180°,且 n 属于正整数. ∴n=10. 则 x=180°×(10-2)-1310°=130°. 故选:B. 6.(2019·广东可园中学中考模拟)如图,在△ABC 中,CD 平分∠ACB 交 AB 于点 D,过点 D 作 DE∥BC 交 AC 于点 E,若∠A=54°,∠B=48°,则∠CDE 的大小为( ) A.44° B.40° C.39° D.38° 【答案】C 【详解】∵∠A=54°,∠B=48°, ∴∠ACB=180°﹣54°﹣48°=78°, ∵CD 平分∠ACB 交 AB 于点 D, ∴∠DCB= 1 2 ×78°=39°, ∵DE∥BC, ∴∠CDE=∠DCB=39°, 故选 C. 7.(2019·辽宁中考模拟)如图,AB∥CD,∠1=45°,∠3=80°,则∠2 的度数为( ) A.30° B.35° C.40° D.45° 【答案】B 【解析】 详解:如图, ∵AB∥CD,∠1=45°, ∴∠4=∠1=45°, ∵∠3=80°, ∴∠2=∠3-∠4=80°-45°=35°, 故选 B. 8.(2018·西藏中考模拟)小华要画一个有两边长分别为 7cm 和 8cm 的等腰三角形,则这个等腰三角形的周 长是( ) A.16cm B.17cm C.22cm 或 23cm D.11cm 【答案】C 【解析】 详解:根据等腰三角形的概念知,有两边相等,因而可以是两条边长为 7 或两条边长为 8.当两条边长为 7 时,周长=7×2+8=22cm;当两条边长为 8 时,周长=8×2+7=23cm. 故选 C. 9.(2018·江苏省无锡金桥双语实验学校中考模拟)△ABC 中,已知点 D,E,F 分别是 BC,AD,CE 边上的中点,且 S△ABC=4cm2 则 S△BEF 的值为( ) A.2cm2 B.1cm2 C.0.5cm2 D.0.25cm2 【答案】B 【解析】 详解:∵点 D、 E 分别是边 BC、AD 上的中点, ∴S△ABD= 1 2 S△ABC,S△ACD= 1 2 S△ABC, S△BDE= 1 2 S△ABD,S△CDE= 1 2 S△ACD, ∴S△BCE=S△BDE+S△CDE= 1 2 S△ABD+ 1 2 S△ACD= 1 2 S△ABC, ∵点 F 是边 CE 的中点, ∴S△BEF= 1 2 S△BCE= 1 2 × 1 2 S△ABC= 1 4 S△ABC, ∵S△ABC=4, ∴S△BFF= 1 4 ×4=1. 故选:B. 10.(2015·四川中考真题)如图,在△ABC 中,∠ABC,∠ACB 的平分线 BE,CD 相交于点 F,∠ABC=42°, ∠A=60°,则∠BFC 的度数为( ) A.118° B.119° C.120° D.121° 【答案】C 【解析】 由三角形内角和定理得∠ABC+∠ACB=120°,由角平分线的性质得∠CBE+∠BCD=60°,再利用三角形的内 角和定理得结果. 解:∵∠A=60°, ∴∠ABC+∠ACB=120°, ∵BE,CD 是∠B、∠C 的平分线, ∴∠CBE= � � ∠ABC,∠BCD= � � ∠BCA, ∴∠CBE+∠BCD= � � (∠ABC+∠BCA)=60°, ∴∠BFC=180°﹣60°=120°, 故选 C. 11.(2018·山东中考真题)如图,直线AB∥EF,点 C是直线 AB 上一点,点 D 是直线 AB 外一点,若∠BCD=95°, ∠CDE=25°,则∠DEF 的度数是( ) A.110° B.115° C.120° D.125° 【答案】C 【解析】 详解:延长 FE 交 DC 于点 N, ∵直线 AB∥EF, ∴∠DNF=∠BCD =95°, ∵∠CDE=25°, ∴∠DEF=95°+25°=120°. 故选:C. 12.(2019·海门市海南中学中考模拟)如图,将直尺与含 30°角的三角尺摆放在一起,若∠1=20°,则∠2 的度数是( ) A.30° B.40° C.50° D.60° 【答案】C 【详解】 ∵∠BEF 是△AEF 的外角,∠1=20°,∠F=30°, ∴∠BEF=∠1+∠F=50°, ∵AB∥CD, ∴∠2=∠BEF=50°, 故选 C. 二、填空题(共 5 小题,每小题 4 分,共 20 分) 13.(2019·四川中考模拟)如图 a 是长方形纸带,∠DEF=25°,将纸带沿 EF 折叠成图 b,再沿 BF 折叠成图 c,则图 c 中的∠CFE 的度数是____________°. 【答案】105° 【解析】 由图 a 知,∠EFC=155°. 图 b 中,∠EFC=155°,则∠GFC=∠EFC-∠EFG=155°-25°=130°. 图 c 中,∠GFC=130°,则∠CFE=130°-25°=105°. 故答案为:105°. 14.(2018·四川中考真题)如图,在△ABC 中,BO、CO 分别平分∠ABC、∠ACB.若∠BOC=110°,则∠ A=_____. 【答案】40° 【详解】 解:∵BO、CO 分别平分∠ABC、∠ACB, ∴∠OBC= 1 2 ∠ABC,∠OCB= 1 2 ∠ACB, 而∠BOC+∠OBC+∠OCB=180°, ∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣ 1 2 (∠ABC+∠ACB), ∵∠A+∠ABC+∠ACB=180°, ∴∠ABC+∠ACB=180°﹣∠A, ∴∠BOC=180°﹣ 1 2 (180°﹣∠A)=90°+ 1 2 ∠A, 而∠BOC=110°, ∴90°+ 1 2 ∠A=110° ∴∠A=40°. 故答案为 40°. 15.(2018·黑龙江中考真题)三角形三边长分别为 3, 2a 1 , 4.则 a 的取值范围是______. 【答案】1 a 4 【详解】 三角形的三边长分别为 3, 2a 1 ,4, 4 3 2a 1 4 3 , 即1 a 4 , 故答案为:1 a 4 . 16.(2019·辽宁中考模拟)如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是 __________. 【答案】180°或 360°或 540° 【解析】 n 边形的内角和是(n-2)•180°, 边数增加 1,则新的多边形的内角和是(4+1-2)×180°=540°, 所得新的多边形的角不变,则新的多边形的内角和是(4-2)×180°=360°, 所得新的多边形的边数减少 1,则新的多边形的内角和是(4-1-2)×180°=180°, 因而所成的新多边形的内角和是 540°或 360°或 180°. 故答案为 540°或 360°或 180°. 17.(2019·河南中考模拟)如图所示,在四边形 ABCD 中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°, 则∠B 的大小是_____. 【答案】40° 【详解】∵∠ADE=60°, ∴∠ADC=120°, ∵AD⊥AB, ∴∠DAB=90°, ∴∠B=360°﹣∠C﹣∠ADC﹣∠A=40°, 故答案为 40°. 三、解答题(共 4 小题,每小题 8 分,共 32 分) 18.(2018·浙江中考模拟)如图,在直角三角形 ABC 中,∠ACB=90° ,CD 是 AB 边上的高,AB=10cm, BC=8cm,AC=6cm,求: (1)CD 的长; (2)△ABC 的角平分线 AE 交 CD 于点 F,交 BC 于 E 点,求证:∠CFE=∠CEF. 【答案】(1)CD= 24 5 ;(2)见解析 【详解】 (1)由题意得,S△ABC= 1 2 ×AB×CD= 1 2 ×AC×BC, ∴ 1 2 ×CD×10= 1 2 ×6×8, 解得 CD= 24 5 ; (2)∵∠ACB=90°, ∴∠CAE+∠CEF=90°, ∵CD 是 AB 边上的高, ∴∠FAD+∠AFD=90°, ∵AE 是∠CAB 的平分线, ∴∠CAE=∠FAD, ∴∠CEF=∠AFD,又∵∠AFD=∠CFE, ∴∠CFE=∠CEF. 19.(2019·湖南中考模拟)如图,∠ABC=38°,∠ACB=100°,AD 平分∠BAC,AE 是 BC 边上的高,求∠ DAE 的度数. 【答案】 31 .DAE 【解析】 试题分析:根据三角形内角和求出∠BAC 的度数,根据角平分线求出∠BAD 的度数,根据外角的性质求出 ∠ADE 的度数,最后根据三角形内角和求出∠DAE 的度数. 试题解析:∵∠ABC=38°,∠ACB=100°(己知) ∴∠BAC=180°―38°―100°=42°(三角形内角和 180°) 又∵AD 平分∠BAC(己知) ∴∠BAD=21° ∴∠ADE=∠ABC+∠BAD=59°(三角形的外角性质) 又∵AE 是 BC 边上的高, 即∠E=90° ∴∠DAE=90°―59°=31° 20.(2017·浙江中考模拟)若方程(x﹣1)(x2﹣2x+m)=0 的三个根可以作为一个三角形的三边之长,则 m 的取值范围: . 【答案】 3 4 <m≤1 【解析】 ∵(x﹣1)(x2﹣2x+m)=0, ∴x﹣1=0 或 x2﹣2x+m=0, ∴原方程的一个根为 1, 设 x2﹣2x+m=0 的两根为 a、b, 则△=4﹣4m≥0,a+b=2,ab=m, 又∴|a﹣b|= = <1, ∴4﹣4m<1, 解得 m> , ∴ <m≤1. 故答案为: <m≤1. 21.(2017·山东郯城红花初中中考模拟)在△ABC 中,AB=AC,AC 上的中线 BD 把三角形的周长分为 24 ㎝和 30 ㎝的两个部分,求三角形的三边长. 【答案】16cm,16 cm,22 cm 或 20 cm,20 cm,14 cm. 【详解】 解:如图所示 设三角形的腰 AB=AC=x cm,分两种情况讨论: (1)若 AB+AD=24cm,则 x+ 1 2 x=24 ∴x=16 ∵三角形的周长为 24+30=54cm 所以三边长分别为 16cm,16 cm,22 cm (2)若 AB+AD=30cm ,则 x+ 1 2 x=30 ∴x=20 ∵三角形的周长为 24+30=54cm ∴三边长分别为 20 cm,20 cm,14 cm 因此,三角形的三边长为 16 cm,16 cm,22 cm 或 20 cm,20 cm,14 cm.查看更多