青岛初中数学七年级上册《1线段的比较与作法》
一、复习:
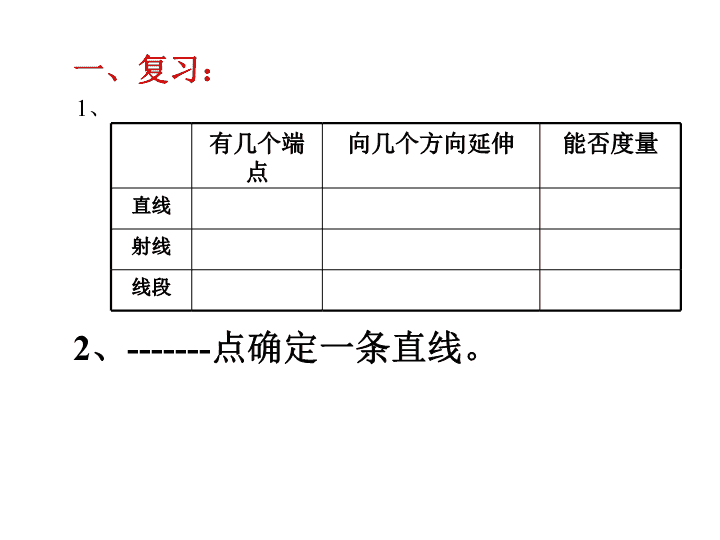
1、
2、-------点确定一条直线。
有几个端
点
向几个方向延伸 能否度量
直线
射线
线段
1.4 线段的比较与作法
学习目标:
1、知道比较线段长短的方法。
2、会比较线段的长短。
3、会用尺规画出线段的和差。
如图,要从甲地到乙地去,有3
条路线,请你选择一条相对近一
些的路?
②
甲地乙地
①
③
从甲地到乙地能否修一条最近的路?
如果能,你认为这条路应该怎样修?
甲地乙地
①
③
②
生活常识告诉我们:
结论 两点之间的所有连线中,线段最短。(简
称两点之间,线段最短)
在图1-29中,用刻度尺量得线段AB的长度为3厘米,
因而A, B两点间的距离为3厘米。
A B
图1-29
3厘米
两点之间线段的长度,叫做这
两点的距离。用刻度尺可以测量线
段的长度。
练一练
错
两点之间线段最短
(1)判断:两点之间的距离是指两点之间的线段。
( )
(2)如图:这是A、B两地之间的公路,在公路工程改造
计划时,为使A、B两地行程最短,应如何设计线路?
在图中画出。你的理由是
B
A
.
3、下列说法正确的是( )
A、连结两点的线段叫做两点间的距离
B、两点间的连线的长度,叫做两点间的距离
C、连结两点的直线的长度,叫做两点的距离
D、连结两点的线段的长度,叫做两点间的距离
D
讨论:
你们平时是如何比较两个同学的身高
的?你能从比身高的方法中得到启示
来比较两条线段的长短吗?
如图1-30,比较点A,B和C两两之间距离的大小。
A B
C
例1
用刻度尺量得线段AB=2.6厘米,线段BC=2.4
厘米,线段CA=2.2厘米。
因为2.2厘米<2.4厘米<2.6厘米,
所以 CA < BC < AB.
解:
连接AB,BC,CA.用刻度尺测量长度,从数量上
比较。
析:
第一种方法是:度量法,
即用一把刻度尺量出两条线段的长度,
再进行比较。
3.1cm
4.1cm
线段的比较:
1 2 3 54 6 7 80
A B
DC
(1)如果点B在线段CD上,
记作AB
CD
(3)如果点B与点D重合,
记作AB=CD
A B
C D
第二种方法:叠合法
注意:起点对齐,看终点。
起点对齐,
看终点
课本练习:
(1)
a
b
(3)
(2)
a b
a
b
观察下列三组图形,分别比较线段a、b的长短。
再用刻度尺量一下,看看你的观察结果是否正确。
尺规作图注意事项:
1、作图语言要规范,
要说明作图结果;
2、保留作图痕迹。 O
线段AB就是所求做的线段.
直尺只用
来画线,
不用来量
距离;
a
A CB
a
尺规作图注意事项:
1、作图语言要规范,
要说明作图结果;
2、保留作图痕迹。
O PB
线段OB就是所求做的线段c
A
已知:线段a,b(如图),用直尺和圆规画一条
线段c,使得它的长度等于两条已知线段的长度
的和。 a b
画法:
1、画射线OP;
2、用圆规在射线OP上截取OA=a ;
3、用圆规在射线AP上截取AC=b。
线段OC的长度就是等于线段a,b的长度和,
即线段OC就是所求的线段c. 记作 OC=a+b
O PA C
线段c的长度是线段a,b的长度的和,我们就说线段c是
线段a,b的和,记做c=a+b;
类似地,线段c是线段a,b的差,记做c=a-b
一看起点,
二看方向,
三看落点。
已知线段a,b,(如图)用尺和圆规画一条线段c,使
它的长度等于a-b。
a
b
合作探究:
画法:
1、画射线OP;
2、用圆规在射线OP上截
取OA=a;
O PA
3、用圆规在线段OA
上截取AB=b;
B
线段OB就是所求作的线段。c=a-b
一看起
点,二
看方向,
三看落
点。
1、如图,填空:
A B C D
AB+BC= ( )AC AD - CD=( )AC
BC=( ) - CDBD AD=( ) + ( ) + ( )AB BC CD
已知线段a,b,画一条线段c,使它的长度等于3a-b
(利用直尺和圆规). a b
画法:
1.画射线AF.
2.用圆规在射线AF上依次截取AB=BC=CD=a.
3. 在线段AD上截取DE=b.
线段AE就是所求的线段c.
A FB C D
a a a
E
b
D
(或 线段AE=3a-b)
2、已知:直线l上有A、B、C三点,且线段
AB=8cm,线段BC=5cm,求线段AC的长。
解:
(1)如图:
(2)如图:
AC=AB+BC =8+5=13cm
AC=AB-BC =8-5=3cm
l
A B C
l
A BC
你能帮小强用这根绳子做一双鞋带吗?
情景活动二
观察下列步骤,并回答问题
(1)拿出一张白纸 (2)对折这张白纸
(3)把白纸展开铺平,发现在边AB上有
个折痕点M,请问AM和BM相等吗? A
B
C
A BM
点M把线段AB分成相等的两条线段AM与
BM,那么点M叫做线段AB的中点
(midpoint),这时AM=BM= AB
,
合作探究
反之,如图,
∵点M是线段AB的中点,
∴AM=BM= AB 或AB=2AM=2BM1
2
线段中点的符号语言表示:
如图, ∵点M在线段AB上且AM=BM
∴点M是线段AB的中点.
2
1
练习:1、如图,已知点C是线段AB的中点,点D是
线段AC的中点,完成下列填空:
(1)AB= _ _ BC ,BC= _ _ AD
(2)BD= _ _ AD
A BCD
2 2
3
反之,
如图,∵点C是线段AB的中点,
∴AC=BC= AB
1
2
线段中点的符号语言表示:
如图,∵点C在线段AB上且AC=BC
∴点C是线段AB的中点.
A BC
2. 如图,AB=6cm,点C是线段AB的中点,点D
是线段CB的中点,那么AD有多长呢?
A DC B
cmCBCD 5.1
2
1
∴AC=CB= cmAB 3
2
1
cmCDACAD 5.4
解:∵点C是线段AB的中点
例1如图
(1)如果点P是AB的中点,
则AP= _ _ AB
(2)如果点C,D三等分AB,则
AC=CD= _ _ = _ _ AB
(4)现在告诉你CP=1.5cm,求线段AB的长。
A BC DP
DB
(3)CP可以表示成哪两条线段的差?你有几种不
同的表示?
1
2
1
3
例:如图,线段AB=8cm,点C是AB的
中点,点D在CB上且DB=1.5cm,求线
段CD的长度。
A C D B
解:CB= AB=4cm,
CD=CB-DB
=4cm-1.5cm=2.5cm.
1
2
如图,线段AB=8cm,点C是AB的
中点,点D是AC的中点,点E是
CB的中点,求线段DE的长度。
解:AC=BC= AB=4cm,
DC= AC=2cm,EC=
CB=2cm,
DE=DC+CE=2cm+2cm=4cm
A BCD E
1
2
1
2
1
2
A
c
C
8
一、学习了怎样比较线段的长短。
1、度量法:
2、叠合法:起点对齐,看终点。
谈谈收获吧
二、尺规作图
1、用尺规法画一条线段等于已知线段;
2、用尺规法画已知线段的和与差。
三、知道线段中点的定义,会用几何符号
表示线段的中点。
一看起点,
二看方向,
三看落点。
希望同学们在今后的学习生活中努力进取,为实现自
己的梦想奋斗!
生命不息,奋斗不止
公元前五世纪的希腊数学家,已经习惯于
用不带刻度的直尺和圆规(以下简称尺规)
来作图了。在他们看来,直线和圆是可以信
赖的最基本的图形,而直尺和圆规是这两种
图形的具体体现,因而只有用尺规作出的图
形才是可信的。于是他们热衷于在尺规限制
下探讨几何作图问题。数学家们总是对用简
单的工具解决困难的问题备加赞赏,自然对
用尺规去画各种图形饶有兴趣。尺规作图是
对人类智慧的挑战,是培养人的思维与操作
能力的有效手段。