- 2021-05-07 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学上册第2章三角形2-5全等三角形第3课时全等三角形判定方法2ASA练习 湘教版
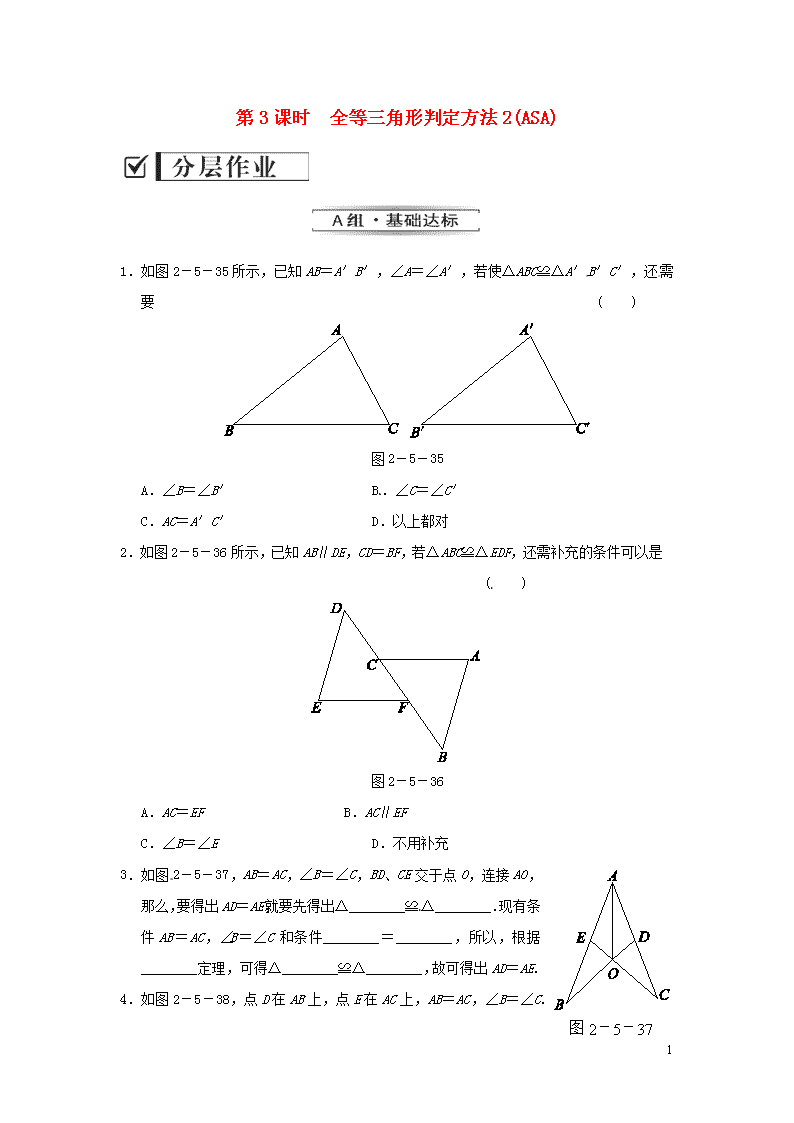
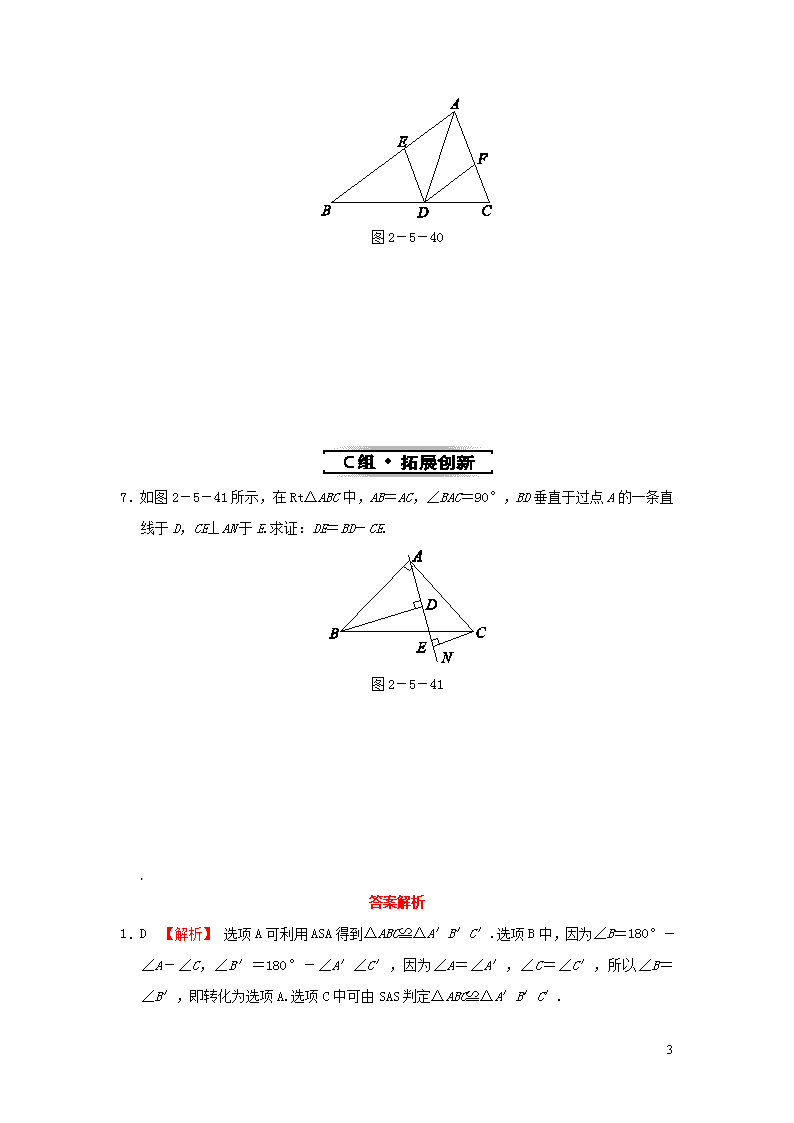
1 第 3 课时 全等三角形判定方法 2(ASA) 1.如图 2-5-35 所示,已知 AB=A′B′,∠A=∠A′,若使△ABC≌△A′B′C′,还需 要 ( ) 图 2-5-35 A.∠B=∠B′ B.∠C=∠C′ C.AC=A′C′ D.以上都对 2.如图 2-5-36 所示,已知 AB∥DE,CD=BF,若△ABC≌△EDF,还需补充的条件可以是 ( ) 图 2-5-36 A.AC=EF B.AC∥EF C.∠B=∠E D.不用补充 3.如图 2-5-37,AB=AC,∠B=∠C,BD、CE 交于点 O,连接 AO, 那么,要得出 AD=AE,就要先得出△________≌ △________.现 有条件 AB=AC,∠B=∠C 和条件________=________,所以,根 据________定理,可得△________≌△________,故可得出 AD= AE. 图 2-5-37 2 4.如图 2-5-38,点 D 在 AB 上,点 E 在 AC 上,AB=AC,∠B=∠C.求证:AD=AE. 图 2-5-38 5.[2011·北京]如图 2-5-39,点 A,C,B,D 在同一条直线上,BE∥DF,∠A=∠F,AB =FD. 求证:AE=FC. 图 2-5-39 6.如图 2-5-40,已知 AD 是△ABC 的角平分线,在不添加任何辅助线的前提下,要使△ AED≌△AFD,还需添加一个条件________,并给予证明. 3 图 2-5-40 7.如图 2-5-41 所示,在 Rt△ABC 中,AB=AC,∠BAC=90°,BD 垂直于过点 A 的一条直 线于 D,CE⊥AN 于 E.求证:DE=BD-CE. 图 2-5-41 答案解析 1.D 【解析】 选项 A 可利用 ASA 得到△ABC≌△A′B′C′.选项 B 中,因为∠B=180°- ∠A-∠C,∠B′=180°-∠A′∠C′,因为∠A=∠A′,∠C=∠C′,所以∠B=∠B′, 即转化为选项 A.选项 C 中可由 SAS 判定△ABC≌△A′B′C′. 4 2.B 【解析】 因为 AB∥DE,所以∠B=∠D.若 AC∥EF,所以∠ACB=∠EFD.又 CD=BF, 所以 DF=BC.根据 ASA 可得△ABC≌△EDF. 3.ADB AEC ∠BAD ∠CAE ASA ADB AEC 4.证明:在△ACD 和△ABE 中, ∠A=∠A, AC=AB, ∠C=∠B, 所以△ACD≌△ABE(ASA). 所以 AD=AE. 5.证明:因为 BE∥DF, 所以∠ABE=∠D. 在△ABE 和△FDC 中, ∠ABE=∠D, AB=FD, ∠A=∠F, [来源:Z&xx&k.Com] 所以△ABE≌△FDC. 所以AE=FC. 6.解法一;添加条件:AE=AF, 证明:在△AED 与△AFD 中, 因为 AE=AF,∠EAD=∠FAD,AD=AD, 所以△AED≌△AFD(SAS). 解法二;添加条件:∠EDA=∠FDA, 证明:在△AED 和△AFD 中, 因为∠EAD=∠FAD,AD=AD,∠EDA=∠FDA, 所以△AED≌△AFD(ASA). 7.【解析】 要证 DE=BD-CE,而 DE=AE-AD,故可想到证 BD=AE,AD=CE,而其分别在 △ABD 与△CAE 中,显然要证明△ABD 与△CAE 全等. 证明:因为∠BAC=90°,BD⊥AN, 所以∠BAD+∠CAE=90°. ∠ABD+∠BAD=90° 所以∠CAE=∠ABD. 5 因为 BD⊥AN,CE⊥AN, 所以∠BDA=∠AEC=90°, 所以∠BAD=∠ACE. 在△ABD 和△CAE 中, ∠BAD=∠ACE, AB=CA, ∠ABD=∠CAE, 所以△ABD≌△CAE(ASA). 所以 BD=AE,AD=CE(全等三角形对应边相等). 因为 DE=AE-AD,所以 DE=BD-CE.查看更多