- 2021-05-06 发布 |
- 37.5 KB |
- 80页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
全国各地中考数学分类解析159套63专题专题63 押轴的解答题专集6
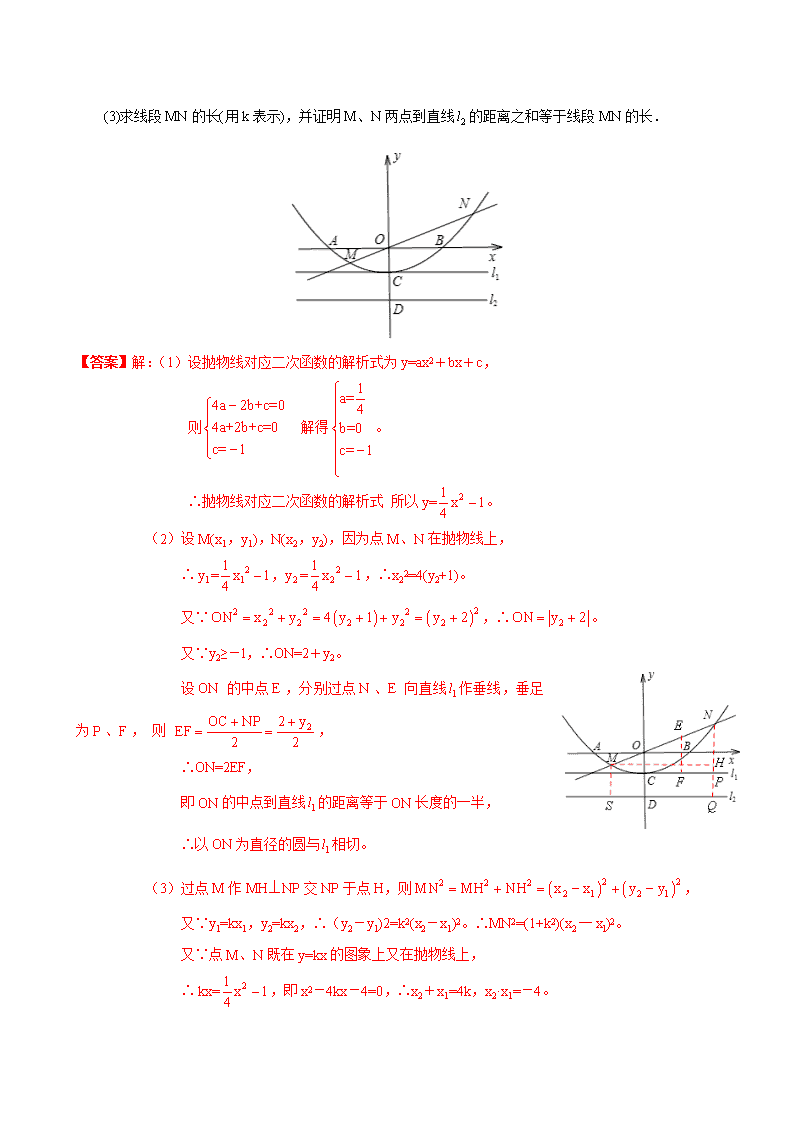
2012年全国中考数学试题分类解析汇编(159套63专题) 专题63:押轴的解答题专集(6) 锦元数学工作室 编辑 三、解答题 251. (2012山东潍坊10分)许多家庭以燃气作为烧水做饭的燃料,节约用气是我们日常生活中非常现实的问题.某款燃气灶旋钮位置从0度到90度(如图),燃气关闭时,燃气灶旋钮的位置为0度,旋钮角度越大,燃气流量越大,燃气开到最大时,旋钮角度为90度.为测试燃气灶旋钮在不同位置上的燃气用量,在相同条件下,选择在燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时,其火力不能够将水烧开,故选择旋钮角度x度的范围是18≤x≤90),记录相关数据得到下表: 旋钮角度(度) 20 50 70 80 90 所用燃气量(升) 73 67 83 97 115 (1)请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律?说明确定是这种函数而不是其它函数的理由,并求出它的解析式; (2)当旋钮角度为多少时,烧开一壶水所用燃气量最少?最少是多少? (3)某家庭使用此款燃气灶,以前习惯把燃气开到最大,现采用最节省燃气的旋钮角度,每月平均能节约燃气10立方米,求该家庭以前每月的平均燃气用量. 【答案】解:(1)若设y=kx+b(k≠0), 由解得 。∴y= x+77。 把x=70代入得y=65≠83,∴一次函数不符合。 若设(k≠0),由解得k=1460。∴ 。 把x=50代入得y=29.2≠67,∴反比例函数不符合。 若设y=ax2+bx+c, 由 解得。∴y=x2 x+97(18≤x≤90)。 把x=80代入得y=97,把x=90代入得y=115,符合题意。 ∴二次函数能表示所用燃气量y升与旋钮角度x度的变化规律。 (2)由(1)得:y=x2 x+97=(x-40)2+65, ∴当x=40时,y取得最小值65。 答:当旋钮角度为40°时,烧开一壶水所用燃气量最少,最少为65升。 (3)由(2)及表格知,采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115-65=50(升),设该家庭以前每月平均用气量为a立方米,则由题意得: ,解得a=23。 答:该家庭以前每月平均用气量为23立方米。 【考点】待定系数法,曲线上点的坐标与方程的关系,二次函数的性质。 【分析】(1)先假设函数为一次函数,任选两点求出函数解析式,再将各点代入验证;再假设函数为二次函数,任选三求出函数解析式,再将各点代入验证 (2)将(1)所求二次函数解析式,化为顶点式,转化为二次函数最值的问题。 (3)由(2)及表格知,采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115-65=50,再设该家庭以前每月平均用气量为a立方米,据此解答即可。 252. (2012山东潍坊11分)如图,已知抛物线与坐标轴分别交于A(-2,O)、B(2,0)、C(0,-l)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)作平行于x轴的直线、. (1)求抛物线对应二次函数的解析式; (2)求证以ON为直径的圆与直线相切; (3)求线段MN的长(用k表示),并证明M、N两点到直线的距离之和等于线段MN的长. 【答案】解:(1)设抛物线对应二次函数的解析式为y=ax2+bx+c, 则 解得。 ∴抛物线对应二次函数的解析式 所以。 (2)设M(x1,y1),N(x2,y2),因为点M、N在抛物线上, ∴,∴x22=4(y2+1)。 又∵,∴。 又∵y2≥-l,∴ON=2+y2。 设ON的中点E,分别过点N、E向直线作垂线,垂足为P、F, 则 , ∴ON=2EF, 即ON的中点到直线的距离等于ON长度的一半, ∴以ON为直径的圆与相切。 (3)过点M作MH⊥NP交NP于点H,则, 又∵y1=kx1,y2=kx2,∴(y2-y1)2=k2(x2-x1)2。∴MN2=(1+k2)(x2一xl)2。 又∵点M、N既在y=kx的图象上又在抛物线上, ∴,即x2-4kx-4=0,∴x2+x1=4k,x2·x1=-4。 ∴MN2=(1+k2)(x2一xl)2=(1+k2)[ (x2+xl)2-4x2·xl] =16(1+k2)2。∴MN=4(1+k2)。 延长NP交于点Q,过点M作MS⊥交于点S, 则MS+NQ=y1+2+y2+2= ∴MS+NQ=MN,即M、N两点到距离之和等于线段MN的长。 【考点】二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,中点坐标的求法,直线与圆相切的条件,一元二次方程根与系数的关系,勾股定理。 【分析】(1)根据点在曲线上,点的坐标满足方程的关系,用待定系数法即可求出抛物线对应二次函数的解析式。 (2)要证以ON为直径的圆与直线相切,只要证ON的中点到直线的距离等于ON长的一半即可。 (3)运用一元二次方程根与系数的关系,求出MN和M、N两点到直线的距离之和,相比较即可。 253. (2012山东烟台10分)(1)问题探究 如图1,分别以△ABC的边AC与边BC为边,向△ABC外作正方形ACD1E1和正方形BCD2E2,过点C 作直线KH交直线AB于点H,使∠AHK=∠ACD1作D1M⊥KH,D2N⊥KH,垂足分别为点M,N.试探究线段D1M与线段D2N的数量关系,并加以证明. (2)拓展延伸 ①如图2,若将“问题探究”中的正方形改为正三角形,过点C作直线K1H1,K2H2,分别交直线AB于点H1,H2,使∠AH1K1=∠BH2K2=∠ACD1.作D1M⊥K1H1,D2N⊥K2H2,垂足分别为点M,N.D1M=D2N是否仍成立?若成立,给出证明;若不成立,说明理由. ②如图3,若将①中的“正三角形”改为“正五边形”,其他条件不变.D1M=D2N是否仍成立?(要求:在 图3中补全图形,注明字母,直接写出结论,不需证明) 【答案】解:(1)D1M=D2N。证明如下: ∵∠ACD1=90°,∴∠ACH+∠D1CK=180°﹣90°=90°。 ∵∠AHK=∠ACD1=90°,∴∠ACH+∠HAC=90°。 ∴∠D1CK=∠HAC。 在△ACH和△CD1M中,∠D1CK=∠HAC,∠AHC=∠C M D1=90°,AC=C D1, ∴△ACH≌△CD1M(AAS)。∴D1M=CH。 同理可证D2N=CH。 ∴D1M=D2N。 (2)①D1M=D2N成立。证明如下: 过点C作CG⊥AB,垂足为点G, ∵∠H1AC+∠ACH1+∠AH1C=180°, ∠D1CM+∠ACH1+∠ACD1=180°,∠AH1C=∠ACD1, ∴∠H1AC=∠D1CM。 在△ACG和△CD1M中,∠H1AC=∠D1CM,∠AGC=∠C M D1=90°,AC=C D1, ∴△ACG≌△CD1M(AAS)。∴CG=D1M。 同理可证CG=D2N。 ∴D1M=D2N。 ②作图如下: D1M=D2N还成立。 【考点】 全等三角形的判定和性质,等边三角形的性质,正方形的性质,正多边形的性质,三角形的内角和定理。 【分析】(1)根据正方形的每一个角都是90°可以证明∠AHK=90°,然后利用平角等于180°以及直角三角形的两锐角互余证明∠D1CK=∠HAC,再利用“角角边”证明△ACH和△CD1M全等,根据全等三角形对应边相等可得D1M=CH,同理可证D2N=CH,从而得证。 (2)①过点C作CG⊥AB,垂足为点G,根据三角形的内角和等于180°和平角等于180°证明得到∠H1AC=∠D1CM,然后利用“角角边”证明△ACG和△CD1M全等,根据全等三角形对应边相等可得CG=D1M,同理可证CG=D2N,从而得证。 ②结论仍然成立,与①的证明方法相同。 254. (2012山东烟台12分)如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E. (1)直接写出点A的坐标,并求出抛物线的解析式; (2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少? (3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值. 【答案】解:(1)A(1,4)。 由题意,设抛物线解析式为y=a(x﹣1)2+4 ∵抛物线过点C(3,0),∴0=a(3﹣1)2+4,解得,a=﹣1。 ∴抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3。 (2)设直线AC的解析式为y=kx+b, ∵A(1,4),C(3,0), ∴,解得。 ∴直线AC的解析式为y=﹣2x+6。 ∵点P(1,4﹣t), ∴将y=4﹣t代入y=﹣2x+6中,解得点E的横坐标为。 ∴点G的横坐标为,代入抛物线的解析式中,可求点G的纵坐标为。 ∴GE=()﹣(4﹣t)=。 又点A到GE的距离为,C到GE的距离为, ∴。 ∴当t=2时,S△ACG的最大值为1。 (3)或。 由题设和(2)知,C(3,0),Q(3,t),E(),设H()。 当CE是对角线时,如图1,有CQ=HE=CH,即 , 解得,或t=4(舍去,此时C,E重合)。 当CE是边时,如图2,有CQ=CE=EH,即 , 解得,或(舍去,此时已超过矩形ABCD的范围)。 综上所述,当或时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形。 255. (2012山东枣庄10分)如图,在平面直角坐标xOy中,一次函数的图象与反比例函数的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,).线段OA=5,E为x轴上一点,且sin∠AOE=. (1)求该反比例函数和一次函数的解析式; (2)求△AOC的面积. 【答案】解:(1)过点A作AD⊥x轴于D点,如图, ∵sin∠AOE=,OA=5,∴sin∠AOE=。 ∴AD=4,∴DO=。 而点A在第二象限,∴点A的坐标为(-3,4)。 将A(-3,4)代入,得m=-12, ∴所求的反比例函数的解析式为。 将B(6,n)代入,得n =-2。 将A(-3,4)和B(6,-2)分别代入,得 ,解得。 ∴所求的一次函数的解析式为。 (2)在中,令,即,解得。 ∴C点坐标为(0,3),即OC=3, ∴。 【考点】反比例函数综合题,曲线上点的坐标与方程的关系,锐角三角函数定义,勾股定理。 【分析】(1)过点A作AD⊥x轴于D点,由sin∠AOE=,OA=5,根据正弦的定义可求出AD,再根据勾股定理得到DO,即得到A点坐标(-3,4),把A(-3,4)代入,即可确定反比例函数的解析式;将B(6,n)代入,确定点B点坐标,然后把A点和B点坐标代入,即可确定一次函数函数的解析式。 (2)先令,求出C点坐标,得到OC的长,然后根据三角形的面积公式计算△AOC的面积即可。 256. (2012山东枣庄10分)在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠 在两坐标轴上,点C为 (-1,0) .如图所示,B点在抛物线y=x2+x-2图象上,过点B作 BD⊥x轴,垂足为D,且B点横坐标为-3. (1)求证:△BDC≌△COA; (2)求BC所在直线的函数关系式; (3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所 有点P的坐标;若不存在,请说明理由. 【答案】解:(1)证明:∵∠BCD+∠ACO=90°,∠ACO+∠OAC=90°, ∴∠BCD=∠OAC。 ∵△ABC为等腰直角三角形 ,∴BC=AC。 在△BDC和△COA中,∠BDC=∠COA=90°,∠BCD=∠OAC,BC=AC, ∴△BDC≌△COA(AAS)。 (2)∵C点坐标为 (-1,0),∴BD=CO=1。 ∵B点横坐标为-3,∴B点坐标为 (-3,1)。 设BC所在直线的函数关系式为y=kx+b, ∴,解得。∴BC所在直线的函数关系式为y=- x- 。 (3)存在 。 ∵y=x2+x-2=(x+)2x-,∴对称轴为直线x=-。 若以AC为直角边,点C为直角顶点,对称轴上有一点P1,使CP1⊥AC, ∵BC⊥AC,∴点P1为直线BC与对轴称直线x=-的交点。 由题意可得: , 解得,。∴P1(-,-)。 若以AC为直角边,点A为直角顶点,对称轴上有一点P2,使AP2⊥AC, 则过点A作A P2∥BC,交对轴称直线x=-于点P2, ∵CD=OA,∴A(0,2)。 设直线AP2的解析式为:y=-x+m,把A(0,2)代入得m=2。 ∴直线AP2的解析式为:y=-x+2。 由题意可得:,解得,。∴P2(-,-)。 ∴P点坐标分别为P1(-,-)、P2(-,-)。 【考点】二次函数综合题,平角定义,直角三角形两锐角的关系,等腰直角三角形的性质,全等三角形的判定和性质,待定系数法,曲线上点的坐标与方程的关系,抛物线的对称轴,直角三角形的判定。 【分析】(1)由等腰直角三角形的性质,平角定义,直角三角形两锐角的关系,可由AAS证得。 (2)求出点B的坐标,由点B、C的坐标,用待定系数法可求BC所在直线的函数关系式。 (3)分点C为直角顶点和点A为直角顶点两种情况讨论即可。 257.(2012山东淄博9分)在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,AB=x. (1)当点G与点D重合时,求x的值; (2)当点F为AD中点时,求x的值及∠ECF的正弦值. 【答案】解:(1)当点G与点D重合时,点F也与点D重合。 ∵矩形ABCD中,AC⊥BD,∴四边形ABCD是正方形。 ∵BC=4,∴x= AB= BC=4。 (2)∵点F为AD中点,BC=4,∴AF=2。 ∵矩形ABCD中,AD∥BC,∴△AEF∽△BEB。∴。 ∴。∴。 ∵矩形ABCD中,∠ABC=∠BAF=900, ∴在Rt△ABC和Rt△BAF中由勾股定理得, 即。 两式相加,得。 又∵AC⊥BG,∴在Rt△ABE中,。 ∴,解得(已舍去负值)。 ∴。 ∴在Rt△CEF中由勾股定理得。 ∴。∴。 【考点】矩形的性质,正方形的判定和性质,相似三角形的判定和性质,勾股定理,锐角三角函数定义。 【分析】(1)由点G与点D重合得出四边形ABCD是正方形即可求得x的值。 (2)由点F为AD中点和矩形的性质,得△AEF∽△BEB,从而得。在Rt△ABC、 Rt△BAF和Rt△ABE应用勾股定理即可求得x的值。在Rt△CEF中应用勾股定理求得CF,根据锐角三角函数定义即可求得∠ECF的正弦值。 258. (2012山东淄博9分)如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4). (1)求反比例函数的解析式; (2)反比例函数的图象与线段BC交于点D,直线过点D,与线段AB相交于点F,求点F的坐标; (3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明. 【答案】解:(1)设反比例函数的解析式, ∵反比例函数的图象过点E(3,4),∴,即。 ∴反比例函数的解析式。 (2)∵正方形AOCB的边长为4,∴点D的横坐标为4,点F的纵坐标为4。 ∵点D在反比例函数的图象上,∴点D的纵坐标为3,即D(4,3)。 ∵点D在直线上,∴,解得。 ∴直线DF为。 将代入,得,解得。∴点F的坐标为(2,4)。 (3)∠AOF=∠EOC。证明如下: 在CD上取CG=CF=2,连接OG,连接EG并延长交x轴于点H。 ∵AO=CO=4,∠OAF=∠OCG=900,AF=CG=2, ∴△OAF≌△OCG(SAS)。∴∠AOF=∠COG。 ∵∠EGB=∠HGC,∠B=∠GCH=900,BG=CG=2, ∴△EGB≌△HGC(AAS)。∴EG=HG。 设直线EG:, ∵E(3,4),G(4,2), ∴,解得,。 ∴直线EG:。 令,得。∴H(5,0),OH=5。 在Rt△AOF中,AO=4,AE=3,根据勾股定理,得OE=5。∴OC=OE。 ∴OG是等腰三角形底边EF上的中线。∴OG是等腰三角形顶角的平分线。 ∴∠EOG=∠GOH。∴∠EOG=∠GOC=∠AOF,即∠AOF=∠EOC。 【考点】反比例函数综合题,待定系数法,曲线上点的坐标与方程的关系,正方形的性质,全等三角形的判定和性质,勾股定理,等腰三角形的判定和性质。 【分析】(1)将点E(3,4)代入待定的反比例函数解析式即可求得反比例函数的解析式。 (2)求出点D的坐标代入即可求出直线DF的解析式,令即可求得点F的坐标。 (3)在CD上取CG=CF=2,连接OG,连接EG并延长交x轴于点H。通过证△OAF≌△OCG(SAS)和△EGB≌△HGC(AAS)得到∠AOF=∠COG和EG=HG。求出直线EG的解析式从而得到点H的坐标,从而得到OH的长。在Rt△AOF中,应用勾股定理求得OE的长。因此得到OG是等腰三角形底边EF上的中线的结论,根据等腰三角形三线合一的性质得OG是等腰三角形顶角的平分线。从而得∠AOF=∠EOC。 259. (2012广西北海10分)如图,AB是O的直径,AE交O于点E,且与O的切线CD互相垂直,垂 足为D。 (1)求证:∠EAC=∠CAB; (2)若CD=4,AD=8: ①求O的半径; ②求tan∠BAE的值。 【答案】(1)证明:连接OC。 ∵CD是⊙O的切线,∴CD⊥OC。 又∵CD⊥AE,∴OC∥AE。∴∠1=∠3。 ∵OC=OA,∴∠2=∠3。 ∴∠1=∠2,即∠EAC=∠CAB。 (2)解:①连接BC。 ∵AB是⊙O的直径,CD⊥AE于点D, ∴∠ACB=∠ADC=90°。 ∵∠1=∠2,∴△ACD∽△ABC。∴。 ∵AC2=AD2+CD2=42+82=80, ∴AB==10。 ∴⊙O的半径为10÷2=5。 ②连接CF与BF。 ∵四边形ABCF是⊙O的内接四边形, ∴∠ABC+∠AFC=180°。 ∵∠DFC+∠AFC=180°,∴∠DFC=∠ABC。 ∵∠2+∠ABC=90°, ∠DFC+∠DCF=90°, ∴∠2=∠DCF。 ∵∠1=∠2,∴∠1=∠DCF。 ∵∠CDF=∠CDF,∴△DCF∽△DAC。∴ 。∴DF==2。 ∴AF=AD-DF=8-2=6。 ∵AB是⊙O的直径,∴∠BFA=90°。 ∴BF==8。∴tan∠BAD=。 【考点】切线的性质,平行的判定和性质,等腰三角形的性质,圆周角定理,勾股定理,相似三角形的判定和性质,锐角三角函数定义。 【分析】(1)连接OC,由CD是⊙O的切线,CD⊥OC,又由CD⊥AE,即可判定OC∥AE,根据平行线的性质与等腰三角形的性质,即可证得∠EAC=∠CAB。 (2)①连接BC,易证得△ACD∽△ABC,根据相似三角形的对应边成比例,即可求得AB的长, 从而可得⊙O的半径长。 ②连接CF与BF.由四边形ABCF是⊙O的内接四边形,易证得△DCF∽△DAC,然后根据 相似三角形的对应边成比例,求得AF的长,又由AB是⊙O的直径,即可得∠BFA是直角,利用勾股定理求得BF的长,即可求得tan∠BAE的值。 260. (2012广西北海12分)如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、 B(0,1)、C(d,2)。 (1)求d的值; (2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图 像上。请求出这个反比例函数和此时的直线B′C′的解析式; (3)在(2)的条件下,直线B′C′交y轴于点G。问是否存在x轴上的点M和反比例函数图像上的点P, 使得四边形PGMC′是平行四边形。如果存在,请求出点M和点P的坐标;如果不存在,请说明理由。 【答案】解:(1)作CN⊥x轴于点N。 在Rt△CNA和Rt△AOB中, ∵NC=OA=2,AC=AB ∴Rt△CNA≌Rt△AOB(HL)。 ∴AN=BO=1,NO=NA+AO=3, 又∵点C在第二象限,∴d=-3。 (2)设反比例函数为,点C′和B′在该比例函数图像上, 设C′(c,2),则B′(c+3,1)。 把点C′和B′的坐标分别代入,得k=2 c;k=c+3。 ∴2 c=c+3,c=3,则k=6。∴反比例函数解析式为。 得点C′(3,2);B′(6,1)。 设直线C′B′的解析式为y=ax+b,把C′、B′两点坐标代入得,解得 。 ∴直线C′B′的解析式为。 (3)设Q是G C′的中点,由G(0,3),C′(3,2),得点Q的横坐标为,点Q的纵坐标为 2+。∴Q(,)。 过点Q作直线l与x轴交于M′点,与的 图象交于P′点,若四边形P′G M′ C′是平行四边形,则有P′Q=Q M′,易知点M′的横坐标大于,点P′的横坐标小于。 作P′H⊥x轴于点H,QK⊥y轴于点K,P′H与QK交于点E,作QF⊥x轴于点F, 则△P′EQ≌△QFM′ 。 设EQ=FM′=t,则点P′的横坐标x为,点P′的纵坐标y为, 点M′的坐标是(,0)。 ∴P′E=。 由P′Q=QM′,得P′E2+EQ2=QF2+FM′2,∴, 整理得:,解得(经检验,它是分式方程的解)。 ∴,,。 ∴P′(,5),M′(,0),则点P′为所求的点P,点M′为所求的点M。 【考点】反比例函数综合题,全等三角形的判定和性质,待定系数法,曲线上点的坐标与方程的关系,平移的性质,平行四边形的和性质,勾股定理,解分式方程和二元一次方程组。 【分析】(1)作CN⊥x轴于点N,由Rt△CNA≌Rt△AOB即可求得d的值。 (2)根据平移的性质,用待定系数法求出反比例函数和直线B′C′的解析式。 (3)根据平行四边形对角线互相平分的性质,取G C′的中点Q,过点Q作直线l与x轴交于M′ 点,与的图象交于P′点,求出P′Q=Q M′的点M′和P′的坐标即可。 261. (2012广西贵港11分)如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且 ∠ACB=90°,AB=5,BC=3。点P在射线AC上运动,过点P作PH⊥AB,垂足为H。 (1)直接写出线段AC、AD以及⊙O半径的长; (2)设PH=x,PC=y,求y关于x的函数关系式; (3)当PH与⊙O相切时,求相应的y值。 【答案】解:(1)AC=4;AD=3,⊙O半径的长为1。 (2)在Rt△ABC中,AB=5,AC=4,则BC=3。 ∵∠C=90°,PH⊥AB,∴∠C=∠PHA=90°。 ∵∠A=∠A, ∴△AHP∽△ACB。∴,即。 ∴,即y与x的函数关系式是。 (3)如图,P′H′与⊙O相切于点M,连接OD,OE,OF,OM。 ∵∠OMH′=∠MH′D=∠H′DO=90°,OM=OD, ∴四边形OMH′D是正方形。∴MH′=OM=1。 ∵CE、CF是⊙O的切线,∠ACB=90°, ∴∠CFO=∠FCE=∠CEO=90°,CF=CE。 ∴四边形CEOF是正方形,CF=OF=1。 ∴P′H′=P′M+MH′=P′F+FC=P′C,即x=y。 又由(2)知,,∴,解得。 【考点】圆的综合题,圆的切线性质,勾股定理,正方形的判定和性质,相似三角形的判定和性质。 【分析】(1)连接AO、DO,EO,FO,设⊙O的半径为r, 在Rt△ABC中,由勾股定理得AC=, ∴⊙O的半径r=(AC+BC-AB)=(4+3-5)=1。 ∵CE、CF是⊙O的切线,∠ACB=90°, ∴∠CFO=∠FCE=∠CEO=90°,CF=CE。∴四边形CEOF是正方形。∴CF=OF=1。 又∵AD、AF是⊙O的切线,∴AF=AD。∴AF=AC-CF=AC-OF=4-1=3,即AD=3。 (2)通过相似三角形△AHP∽△ACB的对应边成比例知, ,将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式。 (3)根据圆的切线定理证得四边形OMH′D、四边形CFOE为正方形;然后利用正方形的性质、圆的切线定理推知P′H′=P′M+MH′=P′F+FC=P′C,即x=y;最后将其代入(2)中的函数关系式即可求得y值。 262. (2012广西贵港12分)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2, -1),交x轴于A、B两点,交y轴于点C,其中点B的坐标为(3,0)。 (1)求该抛物线的解析式; (2)设经过点C的直线与该抛物线的另一个交点为D,且直线CD和直线CA关于直线BC对称,求直线 CD的解析式; (3)在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标;并直接写出此时直线 OP与该抛物线交点的个数。 【答案】解:(1)∵抛物线y=ax2+bx+3的顶点为M(2,-1), ∴设抛物线的解析式为线。 ∵点B(3,0)在抛物线上,∴,解得。 ∴该抛物线的解析式为,即。 (2)在中令x=0,得。∴C(0,3)。 ∴OB=OC=3。∴∠ABC=450。 过点B作BN⊥x轴交CD于点N(如图), 则∠ABC=∠NBC=450。 ∵直线CD和直线CA关于直线BC对称, ∴∠ACB=∠NCB。 又∵CB=CB,∴△ACB≌△NCB(ASA)。 ∴BN=BA。 ∵A,B关于抛物线的对称轴x=2对称,B(3,0), ∴A(1,0)。∴BN=BA=2。∴N(3,2)。 设直线CD的解析式为, ∵C(0,3),N(3,2)在直线CD上, ∴,解得,。 ∴直线CD的解析式为。 (3)设P(2,p)。 ∵M(2,-1),B(3,0),C(0,3), ∴根据勾股定理,得,, 。 ∵PM2+PB2+PC2=35,∴。 整理,得,解得。 ∴P(2,-2)或(2,)。 当P(2,-2)时,直线OP与该抛物线无交点;当P(2,)时,直线OP与该抛物 线有两交点。 【考点】 二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,二次函数的性质,轴对称的性质,全等三角形的判定和性质,勾股定理,一元二次方程根的判别式。 【分析】(1)由于已知抛物线的顶点坐标,所以可设抛物线的顶点式,用待定系数法求解。 (2)由直线CD和直线CA关于直线BC对称,构造全等三角形:过点B作BN⊥x轴交CD于点N,求出点N的坐标,由点B,N的坐标,用待定系数法求出直线CD的解析式。 (3)设P(2,p),根据勾股定理分别求出PM2、PB2和PC2,由PM2+PB2+PC2=35,列式求解即可求得点P的坐标(2,-2)或(2,)。 当P(2,-2)时,直线OP的解析式为,与联立,得, 即。∵△=9-12=-3<0,∴无解,即直线OP与抛物线无交点。 当P(2,)时,直线OP的解析式为,与联立,得, 即。∵△=289-108=181>0,∴有两不相等的实数根,即直线OP与抛物线有两个交点。 263 (2012广西桂林10分)如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连 接A、O1、B、O2. (1)求证:四边形AO1BO2是菱形; (2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2O2D; (3)在(2)的条件下,若△AO2D的面积为1,求△BO2D的面积. 264. (2012广西桂林12分)如图,在△ABC中,∠BAC=90°,AB=AC=6,D为BC的中点. (1)若E、F分别是AB、AC上的点,且AE=CF,求证:△AED≌△CFD; (2)当点F、E分别从C、A两点同时出发,以每秒1个单位长度的速度沿CA、AB运动,到点A、B 时停止;设△DEF的面积为y,F点运动的时间为x,求y与x的函数关系式; (3)在(2)的条件下,点F、E分别沿CA、AB的延长线继续运动,求此时y与x的函数关系式. 【答案】解:(1)证明:∵∠BAC =90°, AB=AC=6,D为BC中点, ∴∠BAD=∠DAC=∠B=∠C=45° 。∴AD=BD=DC= 。 ∵AE=CF,∴△AED≌△CFD(SAS)。 (2)依题意有,FC=AE=x,AF=6-x ∵△AED≌△CFD, ∴ ∴。 ∴。 (3)依题意有:FC=AE=x,AF=BE=x-6,AD=DB,∠ABD=∠DAC=45°, ∴∠DAF=∠DBE=135° 。∴△ADF≌△BDE(SAS)。∴。 ∴。 ∴。 【考点】动点问题,勾股定理,全等三角形的判定和性质,等腰直角三角形的判定和性质,等积变换。 【分析】(1)由已知推出△ABC是等腰直角三角形后易用SAS证得结果。 (2)由△AED≌△CFD,根据等积变换由可得结果。 (3)由△AED≌△CFD,根据等积变换由可得结果。 265. (2012广西河池10分)随着人们环保意识的不断增强,我市家庭电动自行车的拥有量逐年增加.据 统计,某小区2009年底拥有家庭电动自行车125辆,2011年底家庭电动自行车的拥有量达到180辆. (1)若该小区2009年底到2012年底家庭电动自行车拥有量的年平均增长率相同,则该小区到2012年 底电动自行车将达到多少辆? (2)为了缓解停车矛盾,该小区决定投资3万元再建若干个停车位,据测算,建造费用分别为室内车 位1000元/个,露天车位200元/个.考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,则该小区最多可建两种车位各多少个?试写出所有可能的方案. 【答案】解:(1)设家庭电动自行车拥有量的年平均增长率为x,则 125(1+x)2=180,解得x1=0.2=25%,x2=-2.2(不合题意,舍去)。 ∴180(1+20%)=216(辆)。 答:该小区到2012年底家庭电动自行车将达到216辆。 (2)设该小区可建室内车位a个,露天车位b个,则 , 由①得b=150-5a,代入②得20≤a≤ ∵a是正整数,∴a=20或21。 当a=20时b=50;当a=21时b=45。 ∴方案一:建室内车位20个,露天车位50个; 方案二:室内车位21个,露天车位45个。 【考点】一元二次方程和一元一次不等式组的应用。 【分析】(1)设年平均增长率是x,根据某小区2009年底拥有家庭电动自行车125辆,2011年底家庭电动自行车的拥有量达到180辆,可求出增长率,进而可求出到2012年底家庭电动车将达到多少辆。 (2)设建x个室内车位,根据投资钱数可表示出露天车位,根据计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的3倍,可列出不等式组求解,进而可求出方案情况。 266. (2012广西河池12分)如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所 在的直线建立平面直角坐标系,抛物线经过A、B两点. (1)写出点A、点B的坐标; (2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物 线于点E、M和点P,连结PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积; (3)在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P 的坐标;若不存在,请说明理由. 【答案】解:(1)A(8,0),B(0,4)。 (2)∵AB=AC,∴OB=OC。∴C(0,-4)。 设直线AC:,由A(8,0),C(0,-4)得 ,解得。∴直线AC:。 ∵ 直线l移动的速度为2,时间为t,∴OE=2t。 设P, 在中,令x=2t,得,∴M(2t,)。 ∵BC=8,PM=,OE=2t,EA=, ∴ 。 ∴四边形PBCA的面积S与t的函数关系式为(0<t<4)。 ∵, ∴四边形PBCA的最大面积为41个平方单位。 (3)存在。∵由(2),在0<t<4,即0<t<8时,∠AMP和∠APM不可能为直角。 若∠PAM为直角,则PA⊥CA,∴△AOC∽△PEA。∴。 设P,则OC=4,OA=8,EA=8-p,EP=, ∴,整理得,解得(舍去)。 当时,。∴P(3,10)。 ∴当P(3,10)时,△PAM是直角三角形。 【考点】二次函数综合题,动直线问题,待定系数法,曲线上点的坐标与方程的关系,二次函数最值,相似三角形的判定和性质,直角三角形的判定。 【分析】(1)在中,令x=0,得y=4;令y=0,得x=-1或x=8。 ∴A(8,0),B(0,4)。 (2)由AB=AC,根据等腰三角形三线合一的性质可得点C的坐标,从而用待定系数法求出直线AC的解析式,得到点M关于t的表达式,根据求出四边形PBCA的面积S与t 的函数关系式,应用二次函数最值的求法求出四边形PBCA的最大面积。 (3)存在。易知,∠AMP和∠APM不可能为直角。当∠PAM为直角时,△AOC∽△PEA,根据比例关系列出方程求解即可。 267. (2012广西来宾10分)如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E. (1)求证:DE是⊙O的切线; (2)如图AD=5,AE=4,求⊙O的直径. 【答案】(1)证明:如图,连接OD, ∵AD为∠CAB的平分线,∴∠CAD=∠BAD。 又OA=OD,∴∠BAD=∠ODA。∴∠CAD=∠ODA。 ∴AC∥OD。∴∠E+∠EDO=180°。 又AE⊥ED,即∠E=90°,∴∠EDO=90°。 ∴OD为圆O的切线。 (2)解:如图,连接BD, ∵AB为圆O的直径,∴∠ADB=90°。 在Rt△AED中,AE=4,AD=5,∴。 又∵∠EAD=∠DAB,在Rt△ABD中,∴。 ∴,即圆的直径为。 【考点】等腰三角形的性质,平行的判定和性质,切线的判定,圆周角定理,锐角三角函数定义,特殊角的三角函数值。 【分析】(1)连接OD,由AD为角平分线,得到一对角相等,再由OA=OD,得到一对角相等,等量代换得到一对内错角相等,根据内错角相等两直线平行可得AC∥OD,由两直线平行同旁内角互补,得到∠E与∠EDO互补,再由∠E为直角,可得∠EDO为直角,即DE为圆O的切线。 (2)连接BD,由AB为⊙O的直径,根据直径所对的圆周角为直角的性质,得到∠ADB=90°。在 Rt△AED中,由AE和AD的长,根据锐角三角函数定义求出cos∠EAD。又在Rt△ABD中,根据锐角三角函数定义得到 ,即可求出直径AB的长。 268. (2012广西来宾12分)已知抛物线y=ax2+2x+c的图象与x轴交于点A(3,0)和点C,与y轴交于点B(0,3). (1)求抛物线的解析式; (2)在抛物线的对称轴上找一点D,使得点D到点B、C的距离之和最小,并求出点D的坐标; (3)在第一象限的抛物线上,是否存在一点P,使得△ABP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由. 【答案】解:(1)∵抛物线y=ax2+2x+c的图象经过点A(3,0)和点B(0,3), ∴,解得。 ∴抛物线的解析式为:。 (2)∵,∴对称轴为x=1。 令,解得x1=3,x2=-1,∴C(-1,0)。 如图1所示,连接AB,与对称轴x=1的交点即为所求之D点,由于A、C两点关于对称轴对称,则此时DB+DC=DB+DA=AB最小。 设直线AB的解析式为y=kx+b, 由A(3,0)、B(0,3)可得: ,解得。 ∴直线AB解析式为y=-x+3。 当x=1时,y=2,∴D点坐标为(1,2)。 (3)结论:存在。 如图2,设P(x,y)是第一象限的抛物线上一点, 过点P作PN⊥x轴于点N, 则ON=x,PN=y,AN=OA-ON=3-x. ∵P(x,y)在抛物线上,∴,代入上式得: 。 ∴当x= 时,S△ABP取得最大值。 当x= 时,,∴P(, )。 ∴在第一象限的抛物线上,存在一点P,使得△ABP的面积最大,P点的坐标为( ,)。 【考点】二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,二次函数的性质,轴对称的性质。 【分析】(1)利用待定系数法求出抛物线的解析式。 (2)连接AB,与对称轴x=1的交点即为所求之D点.为求D点坐标,求出直线AB的解析式,然后令x=1求得y,即可求出D点坐标。 (3)求出△ABP的面积表达式.这个表达式是一个关于P点横坐标的二次函数,利用二次函数求极值的方法可以确定P点的坐标。 269. (2012广西柳州10分)如图,AB是⊙O的直径,AC是弦. (1)请你按下面步骤画图(画图或作辅助线时先使用铅笔画出,确定后必须使用黑色字迹的签字笔描黑); 第一步,过点A作∠BAC的角平分线,交⊙O于点D; 第二步,过点D作AC的垂线,交AC的延长线于点E. 第三步,连接BD. (2)求证:AD2=AE•AB; (3)连接EO,交AD于点F,若5AC=3AB,求的值. 【答案】解:(1)如图; (2)证明:∵AB是⊙O的直径,∴∠ADB=90°。 又∵DE⊥AC,∴∠AED=90°。 ∵AD平分∠CAB,∴∠CAD=∠DAB。∴Rt△ADE∽Rt△ABD。 ∴AD:AB=AE:AD,∴AD2=AE•AB。 (3)如图,连接OD、BC,它们交于点G, ∵5AC=3AB,即AC:AB=3:5,∴不妨设AC=3x,AB=5x, ∵AB是⊙O的直径,∴∠ACB=90°。∴∠ECG=90°。 又∵∠CAD=∠DAB,∴。∴OD垂直平分BC。 ∴OD∥AE,OG=AC=x。∴四边形ECGD为矩形。 ∴CE=DG=OD-OG=x-x =x。∴AE=AC+CE=3x+x=4x。 ∵AE∥OD,∴△AEF∽△DOF。∴AE:OD=EF:OF,∴EF:OF=4x:x=8:5。 ∴。 【考点】圆的综合题,圆周角定理,相似三角形的判定和性质,垂径定理,矩形的判定和性质。 【分析】(1)根据基本作图作出∠BAC的角平分线AD交⊙O于点D;点D作AC的垂线,垂足为点E。 (2)根据直径所对的圆周角为直角得到∠ADB=90°,DE⊥AC,则∠AED=90°,又由AD平分∠CAB 得到∠CAD=∠DAB,根据相似三角形的判定得到Rt△ADE∽Rt△ABD,根据相似的性质得到AD:AB=AE:AD,利用比例的性质即可得到AD2=AE•AB。 (3)连接OD、BC,它们交于点G,由5AC=3AB,则不妨设AC=3x,AB=5x,根据直径所对的 圆周角为直角得到∠ACB=90°,由∠CAD=∠DAB得到,根据垂径定理的推论得到OD垂直平分BC,则有OD∥AE,OG=AC=x,并且得到四边形ECGD为矩形,则可求出CE,从而计算出AE,利用AE∥OD可得到△AEF∽△DOF,则AE:OD=EF:OF,即EF:OF=4x:x=8:5,然后根据比例的性质即可得到 的值。 270. (2012广西柳州12分)如图,在△ABC中,AB=2,AC=BC=. (1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C 三点的坐标; (2)求过A、B、C三点且以C为顶点的抛物线的解析式; (3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD=S△ABC; (4)如果将(2)中的抛物线向右平移,且与x轴交于点A′B′,与y轴交于点C′,当平移多少个单位时, 点C′同时在以A′B′为直径的圆上(解答过程如果有需要时,请参看阅读材料). 附:阅读材料 一元二次方程常用的解法有配方法、公式法和因式分解法,对于一些特殊方程可以通过换元法转化为一元 二次方程求解.如解方程:y4-4y2+3=0. 解:令y2=x(x≥0),则原方程变为x2-4x+3=0,解得x1=1,x2=3. 当x1=1时,即y2=1,∴y1=1,y2=-1. 当x2=3,即y2=3,∴y3= 3 ,y4=- 3 . 所以,原方程的解是y1=1,y2=-1,y3= 3 ,y4=- 3 . 再如 ,可设 ,用同样的方法也可求解. 【答案】解:(1)∵AB的垂直平分线为y轴,∴OA=OB=AB=×2=1。 ∴A的坐标是(-1,0),B的坐标是(1,0)。 在Rt△OBC中,,∴C的坐标为(0,2)。 (2)设抛物线的解析式是:y=ax2+b, 根据题意得: ,解得: 。 ∴抛物线的解析式是:。 (3)∵S△ABC=AB•OC=×2×2=2,S△ABD=S△ABC,∴S△ABD=S△ABC=1。 设D的纵坐标是m,则AB•|m|=1,∴m=±1。 当m=1时,-2x2+2=1,解得:x=±。 当m=-1时,-2x2+2=-1,解得:x=±。 ∴D的坐标是:(,1)或(-,1)或(,-1),或(-,-1)。 (4)设抛物线向右平移c个单位长度,则0<c≤1,OA′=1-c,OB′=1+c。 平移以后的抛物线的解析式是:。 令x=0,解得y=-2c2+2,即OC′= +2c2+2。 当点C′同时在以A′B′为直径的圆上时有:OC′2=OA′•OB′, 则(-2c2+2)2=(1-c)(1+c),即(4c2-3)(c2-1)=0。 解得:c= ,(舍去),1,-1(舍去)。 故平移 或1个单位长度。 【考点】二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,线段垂直平分线的性质,勾股定理,平移的性质,相似三角形的判定和性质,解多元方程。 【分析】(1)根据y轴是AB的垂直平分线,则可以求得OA,OB的长度,在直角△OAC中,利用勾股 定理求得OC的长度,则A、B、C的坐标即可求解。 (2)利用待定系数法即可求得二次函数的解析式。 (3)首先求得△ABC的面积,根据S△ABD= S△ABC,以及三角形的面积公式,即可求得D的 纵坐标,把D的纵坐标代入二次函数的解析式,即可求得横坐标。 (4)设抛物线向右平移c个单位长度,则0<c≤1,可以写出平移以后的函数解析式,当点C′同 时在以A′B′为直径的圆上时由相似三角形的性质有:OC′2=OA•OB,据此即可得到一个关于c的方程求得c的值。 271. (2012广西南宁10分)如图,已知矩形纸片ABCD,AD=2,AB=4.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O. (1)如图1,求证:A,G,E,F四点围成的四边形是菱形; (2)如图2,当△AED的外接圆与BC相切于点N时,求证:点N是线段BC的中点; (3)如图2,在(2)的条件下,求折痕FG的长. 【答案】解:(1)由折叠的性质可得,GA=GE,∠AGF=∠EGF, ∵DC∥AB,∴∠EFG=∠AGF。∴∠EFG=∠EGF。∴EF=EG=AG。 ∴四边形AGEF是平行四边形(EF∥AG,EF=AG)。 又∵AG=GE,∴四边形AGEF是菱形。 (2)连接ON, ∵△AED是直角三角形,AE是斜边,点O是AE的中点, △AED的外接圆与BC相切于点N, ∴ON⊥BC。 ∵点O是AE的中点,∴ON是梯形ABCE的中位线。 ∴点N是线段BC的中点。 (3)∵OE、ON均是△AED的外接圆的半径,∴OE=OA=ON=2。∴AE=AB=4。 在Rt△ADE中,AD=2,AE=4,∴∠AED=30°。 在Rt△OEF中,OE=2,∠AED=30°,∴。∴FG=。 【考点】翻折变换(折叠问题),折叠对称的性质,菱形的判定,梯形中位线性质,锐角三角函数定义,特殊角的三角函数值。 【分析】(1)根据折叠的性质判断出AG=GE,∠AGF=∠EGF,再由CD∥AB得出∠EFG=∠AGF,从而 判断出EF=AG,得出四边形AGEF是平行四边形,从而结合AG=GE,可得出结论。 (2)连接ON,则ON⊥BC,从而判断出ON是梯形ABCE的中位线,从而可得出结论。 (3)根据(1)可得出AE=AB,从而在Rt△ADE中,可判断出∠AED为30°,在Rt△EFO中求 出FO,从而可得出FG的长度。 272. (2012广西南宁10分)如图,已知矩形纸片ABCD,AD=2,AB=4.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O. (1)如图1,求证:A,G,E,F四点围成的四边形是菱形; (2)如图2,当△AED的外接圆与BC相切于点N时,求证:点N是线段BC的中点; (3)如图2,在(2)的条件下,求折痕FG的长. 【答案】解:(1)由折叠的性质可得,GA=GE,∠AGF=∠EGF, ∵DC∥AB,∴∠EFG=∠AGF。∴∠EFG=∠EGF。∴EF=EG=AG。 ∴四边形AGEF是平行四边形(EF∥AG,EF=AG)。 又∵AG=GE,∴四边形AGEF是菱形。 (2)连接ON, ∵△AED是直角三角形,AE是斜边,点O是AE的中点, △AED的外接圆与BC相切于点N, ∴ON⊥BC。 ∵点O是AE的中点,∴ON是梯形ABCE的中位线。 ∴点N是线段BC的中点。 (3)∵OE、ON均是△AED的外接圆的半径,∴OE=OA=ON=2。∴AE=AB=4。 在Rt△ADE中,AD=2,AE=4,∴∠AED=30°。 在Rt△OEF中,OE=2,∠AED=30°,∴。∴FG=。 【考点】翻折变换(折叠问题),折叠对称的性质,菱形的判定,梯形中位线性质,锐角三角函数定义,特殊角的三角函数值。 【分析】(1)根据折叠的性质判断出AG=GE,∠AGF=∠EGF,再由CD∥AB得出∠EFG=∠AGF,从而 判断出EF=AG,得出四边形AGEF是平行四边形,从而结合AG=GE,可得出结论。 (2)连接ON,则ON⊥BC,从而判断出ON是梯形ABCE的中位线,从而可得出结论。 (3)根据(1)可得出AE=AB,从而在Rt△ADE中,可判断出∠AED为30°,在Rt△EFO中求 出FO,从而可得出FG的长度。 273. (2012广西钦州10分)如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC. (1)求证:EF是⊙O的切线; (2)求证:AC2=AD•AB; (3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积. 【答案】解:(1)证明:连接OC, ∵OA=OC,∴∠BAC=∠OCA。 ∵∠DAC=∠BAC,∴∠OCA=∠DAC。∴OC∥AD。 ∵AD⊥EF,∴OC⊥EF。 ∵OC为半径,∴EF是⊙O的切线。 (2)证明:∵AB为⊙O直径,AD⊥EF, ∴∠BCA=∠ADC=90°。 ∵∠DAC=∠BAC,∴△ACB∽△ADC。 ∴。∴AC2=AD•AB。 (3)∵∠ACD=30°,∠OCD=90°,∴∠OCA=60°. ∵OC=OA,∴△OAC是等边三角形。∴AC=OA=OC=2,∠AOC=60°。 ∵在Rt△ACD中,AD=AC=1。 由勾股定理得:DC=, ∴阴影部分的面积是S=S梯形OCDA﹣S扇形OCA=×(2+1)×﹣。 【考点】圆的综合题,等腰(边)三角形的判定和性质,平行的判定和性质,切线的判定,圆周角定理,相似三角形的判定和性质,解直角三角形,扇形面积。 【分析】(1)连接OC,根据OA=OC推出∠BAC=∠OCA=∠DAC,推出OC∥AD,得出OC⊥EF,根据切线的判定推出即可。 (2)证△ADC∽△ACB,得出比例式,即可推出答案。 (3)求出等边三角形OAC,求出AC、∠AOC,在Rt△ACD中,求出AD、CD,求出梯形OCDA和扇形OCA的面积,相减即可得出答案。 274. (2012广西钦州12分)如图甲,在平面直角坐标系中,A、B的坐标分别为(4,0)、(0,3),抛物线y=x2+bx+c经过点B,且对称轴是直线x=﹣. (1)求抛物线对应的函数解析式; (2)将图甲中△ABO沿x轴向左平移到△DCE(如图乙),当四边形ABCD是菱形时,请说明点C和点D都在该抛物线上. (3)在(2)中,若点M是抛物线上的一个动点(点M不与点C、D重合),经过点M作MN∥y轴交直线CD于N,设点M的横坐标为t,MN的长度为l,求l与t之间的函数解析式,并求当t为何值时,以M、N、C、E为顶点的四边形是平行四边形.(参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(,),对称轴是直线x=.) 【答案】解:(1)由于抛物线y=x2+bx+c与y轴交于点B(0,3),则 c=3。 ∵抛物线的对称轴 x=,∴b=5a=。 ∴抛物线的解析式:y=x2+x+3。 (2)∵A(4,0)、B B(0,3),∴OA=4,OB=3,。 若四边形ABCD是菱形,则 BC=AD=AB=5,∴C(﹣5,3)、D(﹣1,0). 将C(﹣5,3)代入y=x2+x+3中,得:×(﹣5)2+×(﹣5)+3=3, ∴点C在抛物线上; 同理可证:点D也在抛物线上。 (3)设直线CD的解析式为:y=kx+b,依题意,有: ,解得。∴直线CD:y=x。 由于MN∥y轴,设 M(t,t2+t+3),则 N(t,t )。 ①t<﹣5或t>﹣1时,l=MN=(t2+t+3)﹣(t )=t2+t+; ②﹣5<t<﹣1时,l=MN=(t )﹣(t2+t+3)=﹣t2﹣t﹣。 若以M、N、C、E为顶点的四边形是平行四边形,由于MN∥CE,则MN=CE=3,则有: t2+t+=3,解得:t=﹣3±2;或﹣t2﹣t﹣=3,解得:t=﹣3。 综上所述,l与t之间的函数解析式为l=。 且当t=﹣3±2或﹣3时,以M、N、C、E为顶点的四边形是平行四边形。 【考点】二次函数综合题,二次函数的性质,待定系数法,曲线上点的坐标与方程的关系,勾股定理,菱形的性质,平行四边形的判定。 【分析】(1)抛物线y=x2+bx+c中,(0,c)代表的是抛物线与y轴的交点,x=是抛物线的对称轴,据此确定待定系数。 (2)已知A、B点的坐标,由勾股定理能求出AB的长,若四边形ABCD是菱形,那么AD=BC=AB,可据此求出C、D点的坐标,再代入抛物线的解析式中进行验证即可。 (3)在求l与t之间的函数解析式时,要分两种情况:①抛物线在直线CD上方、②抛物线在直线CD下方;先根据直线CD与抛物线的解析式,表示出M、N的坐标,它们纵坐标的差即为l的长,当以M、N、C、E为顶点的四边形是平行四边形时,由于CE∥MN∥y轴,那么CE必与MN相等,将CE长代入l、t的函数关系式中,即可求出符合条件的t的值。 275. (2012广西玉林、防城港10分)如图,在平面直角坐标系O中,梯形AOBC的边OB在轴的正半轴上,AC//OB,BC⊥OB,过点A的双曲线的一支在第一象限交梯形对角线OC于点D,交边BC于点E. (1)填空:双曲线的另一支在第 象限,的取值范围是 ; (2)若点C的坐标为(2,2),当点E 在什么位置时,阴影部分面积S最小? (3)若,S△OAC=2 ,求双曲线的解析式. 【答案】解:(1)三,k>0, (2)∵梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB, 而点C的坐标标为(2,2), ∴A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0), 把y=2代入得;把x=2代入得。 ∴A点的坐标为(,2),E点的坐标为(2,)。 ∴。 当k=2时,S阴影部分最小,最小值为1.5。 此时E点的坐标为(2,1),即E点为BC的中点。 ∴当点E在BC的中点时,阴影部分的面积S最小。 (3)设D点坐标为(a,), ∵,∴OD=DC,即D点为OC的中点。∴C点坐标为(2a,)。 ∴A点的纵坐标为。 把y=代入得x=,∴A点坐标为(,), 又∵S△OAC=2,∴×(2a-)×=2,∴k=。 ∴双曲线的解析式为。 【考点】反比例函数综合题,反比例函数图象与性质,曲线上点的坐标与方程的关系,梯形的性质,二次函数的最值。 【分析】(1)根据反比例函数图象与性质得到:双曲线 的一支在第一象限,则k>0,得到另一支在第三象限。 (2)根据梯形的性质,AC∥x轴,BC⊥x轴,而点C的坐标为(2,2),则A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0),再分别把y=2或x=2代入可得到A点的坐标和E点的坐标,然后计算出阴影部分面积S关于k的二次函数关系式,应用二次函数的最值求法即可求得阴影部分面积S最小时点E 的位置。 (3)设D点坐标为(a,),由得OD=DC,即D点为OC的中点,从而可得 C点坐标为(2a,),得到A点的纵坐标为,代入 可确定A点坐标为(,),根据三角形面积公式由S△OAC=2列式求解即可求出k的值,从而得到双曲线的解析式。 276. (2012广西玉林、防城港12分)如图,在平面直角坐标系O中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t秒,当t=2秒时PQ=. (1)求点D的坐标,并直接写出t的取值范围; (2)连接AQ并延长交轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值. (3)在(2)的条件下,t为何值时,四边形APQF是梯形? 【答案】解:(1)由题意可知,当t=2(秒)时,OP=4,CQ=2, 在Rt△PCQ中,由勾股定理得:PC==4, ∴OC=OP+PC=4+4=8。[来源:Zxxk.Com] 又∵矩形AOCD,A(0,4),∴D(8,4)。 t的取值范围为:0<t<4。 (2)结论:△AEF的面积S不变化。 ∵AOCD是矩形,∴AD∥OE,∴△AQD∽△EQC。 ∴,即,解得CE=。 由翻折变换的性质可知:DF=DQ=4-t,则CF=CD+DF=8-t。 S=S梯形AOCF+S△FCE-S△AOE=(OA+CF)•OC+CF•CE-OA•OE = [4+(8-t)]×8+(8-t)•-×4×(8+)。 化简得:S=32为定值。 所以△AEF的面积S不变化,S=32。 (3)若四边形APQF是梯形,因为AP与CF不平行,所以只有PQ∥AF。 由PQ∥AF可得:△CPQ∽△DAF。 ∴CP:AD=CQ:DF,即8-2t:8= t:4-t,化简得t2-12t+16=0, 解得:t1=6+2,t2=。 由(1)可知,0<t<4,∴t1=6+2不符合题意,舍去。 ∴当t=秒时,四边形APQF是梯形。:Z*xx*k.Com] 【考点】动点和翻折问题,矩形的性质,勾股定理,翻折对称的性质,相似三角形的判定和性质,梯形的性质,解一元二次方程。 【分析】(1)由勾股定理可求PC而得点C的坐标,根据矩形的性质可得点D的坐标。点P到达终点所需时间为8÷2=4秒,点Q到达终点所需时间为4÷1=4秒,由题意可知,t的取值范围为:0<t<4。 (2)根据相似三角形和翻折对称的性质,求出S关于t的函数关系式,由于关系式为常数,所以△AEF的面积S不变化,S=32。 (3)根据梯形的性质,应用相似三角形即可求解。 277. (2012云南省7分)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN. (1)求证:四边形BMDN是菱形; (2)若AB=4,AD=8,求MD的长. 【答案】解:(1)证明:∵四边形ABCD是矩形,∴AD∥BC。∴∠BNO=∠DMO,∠NBO=∠MDO。 ∵MN是BD的中垂线,∴OB=OD,BD⊥MN。 ∴△BNO≌△DMO(AAS)。∴ON=OM。 ∴四边形BMDN的对角线互相平分。∴四边形BMDN是平行四边形。 ∵BD⊥MN,∴平行四边形BMDN是菱形。 (2)∵四边形BMDN是菱形,∴MB=MD。 设MD长为x,则MB=DM=x,AM=8-x。 ∵四边形ABCD是矩形,∴∠A=900。 在Rt△AMB中,BM2=AM2+AB2,即x2=(8-x)2+42,解得:x=5。 答:MD长为5。 【考点】矩形的性质,线段垂直平分线的性质,平行四边形的性质,菱形的判定和性质,全等三角形的判定和性质,勾股定理。 【分析】(1)根据矩形性质求出AD∥BC,根据OB=OD和AD∥BC推出△BNO≌△DMO ,OM=ON,得出平行四边形BMDN,推出菱形BMDN。 (2)根据菱形性质求出DM=BM,在Rt△AMB中,根据勾股定理得出BM2=AM2+AB2,推出 x2=x2-16x+64+16,求出即可。 278. (2012云南省9分)如图,在平面直角坐标系中,直线交x轴于点P,交y轴于点A.抛物线的图象过点E(-1,0),并与直线相交于A、B两点. (1)求抛物线的解析式(关系式); (2)过点A作AC⊥AB交x轴于点C,求点C的坐标; (3)除点C外,在坐标轴上是否存在点M,使得△MAB是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由. 【答案】解:(1)∵一次函数交y轴于点A, ∴令x=0,得y=2。∴A(0,2)。 ∵A(0,2)、E(-1,0)是抛物线的图象上的点, ∴,解得 。 ∴抛物线的解析式是:。 (2)∵一次函数交x轴于点P,∴令y=0,得x=6。∴P(6,0)。 ∵AC⊥AB,OA⊥OP,∴△AOC∽△POA。∴。 ∵AO=2,PO=6,∴。∴。∴点C的坐标为。 (3)存在。 设除点C外,在坐标轴上还存在点M,使得△MAB是直角三角形, 即∠AMB=900或∠ABM=900。 ∵点B是直线和抛物线的交点, ∴,解得。∴。 ①若∠AMB=900,那么点M是以AB为直径的圆与坐标轴的交点,这时点M会在x轴的正半轴上和y轴的正半轴上。 若交点在y轴的正半轴上(如图),则点M的纵坐标与点B的纵坐标相等,即。 若交点在x轴的正半轴上(如图),设,过点B作BD⊥x轴于点D,则有△AOM∽△MDA。∴ 。 ∵AO=2,MD=,OM=m,DB=, ∴,解得。∴或。 ⑵若∠ABM=900,即过B作BM⊥AP,这时M在x轴的正半轴上和y轴的负半轴上。 若交点在x轴的正半轴上(如图),设,过点B作BD⊥x轴于点D,则有△BDM∽△PDB。∴ 。 ∵BD=,MD=,PD=, ∴,解得。∴。 若交点在y轴的负半轴上(如图),设,过B作BF垂直y轴于点F,则有△ABF∽△BMF。∴ 。 ∵BF=,AF=,MF=, ∴,解得。 ∴。 综上所述,除点C外,在坐标轴上还存在点M,使得△MAB是直角三角形,满足条件 的点M的坐标是:、或、或、或,或共五个点。 【考点】二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,一次、二次函数的性质,相似三角形的判定和性质,直角三角形的判定。 【分析】(1)求出点A的坐标,由点A、E在抛物线的图象上,用待定系数法即可求得抛物线的解析式。 (2)由△AOC∽△POA得比例式即可求得点C的坐标。 (3)分∠AMB=900(交点在y轴的正半轴上或交点在x轴的正半轴上),∠ABM=900(交点在x轴的正半轴上或交点在y轴的负半轴上)讨论即可。 279. (2012河北省10分)如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°, CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒. (1)求点C的坐标; (2)当∠BCP=15°时,求t的值; (3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值. 【答案】解:(1)∵∠BCO=∠CBO=45°,∴OC=OB=3。 又∵点C在y轴的正半轴上,∴点C的坐标为(0,3)。 (2)分两种情况考虑: ①当点P在点B右侧时,如图2, 若∠BCP=15°,得∠PCO=30°,故PO=CO•tan30°=。此时t=4+ ②当点P在点B左侧时,如图3, 由∠BCP=15°,得∠PCO=60°,故OP=COtan60°=3。此时,t=4+3 ∴t的值为4+或4+3 (3)由题意知,若⊙P与四边形ABCD的边相切时,有以下三种情况: ①当⊙P与BC相切于点C时,有 ∠BCP=90°,从而∠OCP=45°,得到OP=3,此时t=1。 ②当⊙P与CD相切于点C时,有 PC⊥CD,即点P与点O重合,此时t=4。 ③当⊙P与AD相切时,由题意,得 ∠DAO=90°,∴点A为切点,如图4,PC2=PA2=(9-t)2,PO2=(t-4)2。 于是(9-t)2= PO2=(t-4)2,即81-18t+t2=t2-8t+16+9,解得,t=5.6。 综上所述,t的值为1或4或5.6。 【考点】动点问题,切线的性质,坐标与图形性质,矩形的性质,勾股定理,锐角三角函数定义,特殊角的三角函数值。 【分析】(1)由∠CBO=45°,∠BOC为直角,得到△BOC为等腰直角三角形,又OB=3,利用等腰直角三角形AOB的性质知OC=OB=3,然后由点C在y轴的正半轴可以确定点C的坐标。 (2)分点P在点B右侧和点P在点B左侧两种情况讨论即可。 (3)当⊙P与四边形ABCD的边(或边所在的直线)相切时,分三种情况讨论:①当⊙P与BC边相切时,②当⊙P与CD相切于点C时,③当⊙P与CD相切时。 280. (2012河北省12分)如图1和2,在△ABC中,AB=13,BC=14,cos∠ABC=. 探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积S△ABC= ; 拓展:如图2,点D在AC上(可与点A,C重合),分别过点A、C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为S△ABD=0) (1)用含x,m,n的代数式表示S△ABD及S△CBD; (2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值; (3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围. 发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值. 【答案】解:探究:12;15;84。 拓展:(1)由三角形面积公式,得 ,。 (2)由(1)得,, ∴ ∵△ABC中AC边上的高为, ∴x的取值范围为。 ∵随x的增大而减小, ∴当时,的最大值为15,当时,的最小值为12。 (3)x的取值范围为或。 发现:直线AC,A、B、C三点到这条直线的距离之和最小,最小值为。 【考点】动点问题,锐角三角函数定义,特殊角有三角函数值,勾股定理, 垂直线段的性质,反比例函数的性质。 【分析】探究:在Rt△ABH中,AB=13,,∴BH=AB。 ∴根据勾股定理,得。 ∵BC=14,∴HC=BC-BH=9。∴根据勾股定理,得。 ∴。 拓展:(1)直接由三角形面积公式可得。 (2)由(1)和即可得到关于x的反比例函数关系式。根据垂直线段最短的性质,当BD⊥AC时,x最小,由面积公式可求得;因为AB=13,BC=14,所以当BD=BC=14时,x最大。从而根据反比例函数的性质求出m+n)的最大值和最小值。 (3)当时,此时BD⊥AC,在线段AC上存在唯一的点D;当时,此时在线段AC上存在两点D;当时,此时在线段AC上存在唯一的点D。因此x的取值范围为或。 发现:由拓展(2)知,直线AC,A、B、C三点到这条直线的距离之和(即△ABC中AC边上的高)最小,最小值为(它小于BC边上的高12和AB边上的高)。 281. (2012河南省10分)类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整. 原题:如图1,在□ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若,求的值。 (1)尝试探究 在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,的值是 (2)类比延伸 如图2,在原题的条件下,若则的值是 (用含的代数式表示),试写出解答过程。 (3)拓展迁移 如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若 ABCD,则的值是 (用a,b含的代数式表示). 【答案】解:(1)AB=3EH;CG=2EH;。 (2)。 如图,作EH∥AB交BG于点H,则△EFH∽△AFB。 ∴。∴AB=mEH。 ∵AB=CD,∴CD=mEH 。 ∵EH∥AB∥CD,∴△BEH∽△BCG。 ∴。∴CG=2EH。 ∴。 (3)ab。 【考点】平行四边形的性质,相似三角形的判定和性质,二次函数的最值。 【分析】(1)本问体现“特殊”的情形, 是一个确定的数值。 依题意,如图,过点E作EH∥AB交BG于点H, 则有△ABF∽△HEF。∴。∴AB=3EH。 ∵□ABCD,EH∥AB,∴EH∥CD。 又∵E为BC中点,∴EH为△BCG的中位线,∴CG=2EH,。 (2)本问体现“一般”的情形, 不再是一个确定的数值,但(1)问中的解题方法依然适用。 (3)本问体现“类比”与“转化”的情形,将(1)(2)问中的解题方法推广转化到梯形中: 如图所,过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD。 ∵EH∥CD,∴△BCD∽△BEH。 ∴。∴CD=bEH。 又∵,∴AB=aCD=abEH。 ∵EH∥AB,∴△ABF∽△EHF。∴ 。 282. (2012河南省11分)如图,在平面直角坐标系中,直线与抛物线交于A,B两点,点A在x轴上,点B的纵坐标为3。点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D (1)求a,b及的值 (2)设点P的横坐标为 ①用含的代数式表示线段PD的长,并求出线段PD长的最大值; ②连接PB,线段PC把△PDB分成两个三角形,是否存在适合的值,使这两个三角形的面积之比为9:10?若存在,直接写出值;若不存在,说明理由. 【答案】解:(1)由,得到x=-2,∴A(-2,0)。 由,得到x=4,∴B(4,3)。 ∵经过A、B两点, ∴,解得。 设直线AB与y轴交于点E,则E(0,1)。 ∴根据勾股定理,得AE=。 ∵PC∥y轴,∴∠ACP=∠AEO。 ∴。 (2)①由(1)可知抛物线的解析式为。 由点P的横坐标为,得P,C。 ∴PC= 。 在Rt△PCD中,, ∵,∴当m=1时,PD有最大值。 ②存在满足条件的值,。 【考点】二次函数综合题,曲线上点的坐标与方程的关系,勾股定理,平行的性质,锐角三角函数定义,二次函数最值。 【分析】(1)求出点A、B的坐标,代入即可求出a,b。由PC∥y轴,得∠ACP=∠AEO,在Rt△AOE中应用锐角三角函数定义即可求得。 (2)①用表示出点P、C的坐标,从而表示出PC的长:PC,由锐角三角函数定义得,代入即能用含的代数式表示线段PD的长。根据二次函数最值求法求得线段PD长的最大值。 ②如图,分别过点D,B作DF⊥PC,BG⊥PC,垂足分别为F,G。 ∵,∴设DP= k,CP=5 k。 ∴根据勾股定理,得DC=k。∴。 在Rt△PDF中,。 又BG=4-m, ∴。 当时,解得; 当时,解得。 283. (2012新疆区12分)库尔勒某乡A,B两村盛产香梨,A村有香梨200吨,B村有香梨300吨,现将这些香梨运到C,D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元.设从A村运往C仓库的香梨为x吨,A,B两村运香梨往两仓库的运输费用分别为yA元,yB元. (1)请填写下表,并求出yA,yB与x之间的函数关系式; C D 总计 A x吨 200吨 B 300吨 总计 240吨 260吨 500吨 (2)当x为何值时,A村的运费较少? (3)请问怎样调运,才能使两村的运费之和最小?求出最小值. 【答案】解:(1)填表如下: C D 总计 A x吨 (200﹣x)吨 200吨 B (240﹣x)吨 (60+x)吨 300吨 总计 240吨 260吨 500吨 由题意得:yA=40x+45(200﹣x)=﹣5x+9000; yB=25(240﹣x)+32(60+x)=7x+7920。 (2)对于yA=﹣5x+9000(0≤x≤200), ∵k=﹣5<0,∴此一次函数为减函数, ∴当x=200吨时,yA最小,其最小值为﹣5×200+9000=8000(元)。 (3)设两村的运费之和为W(0≤x≤200), 则W=yA+yB=﹣5x+9000+7x+7920=2x+16920, ∵k=2>0,∴此一次函数为增函数, ∴当x=0时,W有最小值,W最小值为16920元。 ∴按如下方案调运,两村的运费之和最小,最小值为16920元。 C D A 0吨 200吨 B 40吨 240吨 【考点】一次函数的应用。 【分析】(1)由A村共有香梨200吨,从A村运往C仓库x吨,剩下的运往D仓库,故运往D仓库为(200﹣x)吨,由A村已经运往C仓库x吨,C仓库可储存240吨,故B村应往C仓库运(240﹣x)吨,剩下的运往D仓库,剩下的为300﹣(240﹣x),化简后即可得到B村运往D仓库的吨数,填表即可。 由从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别 为每吨25元和32元,由表格中的代数式,即可分别列出yA,yB与x之间的函数关系式。 (2)由第一问表示出的yA与x之间的函数关系式得到此函数为一次函数,根据x的系数为负数,得到此一次函数为减函数,且0≤x≤200,故x取最大200时,yA有最小值,即为A村的运费较少时x的值。 (3)设两村的运费之和为W,W=yA+yB,把第一问表示出的两函数解析式代入,合并后得到W为关于x的一次函数,且x的系数大于0,可得出此一次函数为增函数,可得出x=0时,W有最小值,将x=0代入W关于x的函数关系式中,即可求出W的最小值。 284. (2012新疆区12分)库尔勒某乡A,B两村盛产香梨,A村有香梨200吨,B村有香梨300吨,现将这些香梨运到C,D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元.设从A村运往C仓库的香梨为x吨,A,B两村运香梨往两仓库的运输费用分别为yA元,yB元. (1)请填写下表,并求出yA,yB与x之间的函数关系式; C D 总计 A x吨 200吨 B 300吨 总计 240吨 260吨 500吨 (2)当x为何值时,A村的运费较少? (3)请问怎样调运,才能使两村的运费之和最小?求出最小值. 【答案】解:(1)填表如下: C D 总计 A x吨 (200﹣x)吨 200吨 B (240﹣x)吨 (60+x)吨 300吨 总计 240吨 260吨 500吨 由题意得:yA=40x+45(200﹣x)=﹣5x+9000; yB=25(240﹣x)+32(60+x)=7x+7920。 (2)对于yA=﹣5x+9000(0≤x≤200), ∵k=﹣5<0,∴此一次函数为减函数, ∴当x=200吨时,yA最小,其最小值为﹣5×200+9000=8000(元)。 (3)设两村的运费之和为W(0≤x≤200), 则W=yA+yB=﹣5x+9000+7x+7920=2x+16920, ∵k=2>0,∴此一次函数为增函数, ∴当x=0时,W有最小值,W最小值为16920元。 ∴按如下方案调运,两村的运费之和最小,最小值为16920元。 C D A 0吨 200吨 B 40吨 240吨 【考点】一次函数的应用。 285. (2012江西南昌8分)如图,已知二次函数L1:y=x2﹣4x+3与x轴交于A.B两点(点A在点B左边),与y轴交于点C. (1)写出二次函数L1的开口方向、对称轴和顶点坐标; (2)研究二次函数L2:y=kx2﹣4kx+3k(k≠0). ①写出二次函数L2与二次函数L1有关图象的两条相同的性质; ②若直线y=8k与抛物线L2交于E、F两点,问线段EF的长度是否发生变化?如果不会,请求出EF的长度;如果会,请说明理由. 【答案】解:(1)∵抛物线, ∴二次函数L1的开口向上,对称轴是直线x=2,顶点坐标(2,﹣1)。 (2)①二次函数L2与L1有关图象的两条相同的性质: 对称轴为x=2;都经过A(1,0),B(3,0)两点。 ②线段EF的长度不会发生变化。 ∵直线y=8k与抛物线L2交于E、F两点, ∴kx2﹣4kx+3k=8k,∵k≠0,∴x2﹣4x+3=8。解得:x1=﹣1,x2=5。 ∴EF=x2﹣x1=6。∴线段EF的长度不会发生变化。 【考点】二次函数综合题,二次函数的性质。 【分析】(1)抛物线y=ax2+bx+c中:a的值决定了抛物线的开口方向,a>0时,抛物线的开口向上;a<0时,抛物线的开口向下。抛物线的对称轴方程和顶点坐标,可化为顶点式或用公式求解。 (2)①新函数是由原函数的各项系数同时乘以k所得,因此从二次函数的图象与解析式的系数的关系入手进行分析。 ②联立直线和抛物线L2的解析式,先求出点E、F的坐标,从而可表示出EF的长,若该长度为定值,则线段EF的长不会发生变化。 286. (2012江西南昌12分)已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作. (1)①折叠后的所在圆的圆心为O′时,求O′A的长度; ②如图2,当折叠后的经过圆心为O时,求的长度; ③如图3,当弦AB=2时,求圆心O到弦AB的距离; (2)在图1中,再将纸片⊙O沿弦CD折叠操作. ①如图4,当AB∥CD,折叠后的与所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值; ②如图5,当AB与CD不平行,折叠后的与所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论. 【答案】解:(1)①折叠后的所在圆O′与⊙O是等圆,∴O′A=OA=2。 ②当经过圆O时,折叠后的所在圆O′在⊙O上,如图2所示,连接O′A.OA.O′B,OB,OO′。 ∵△OO′A,△OO′B为等边三角形,∴∠AO′B=∠AO′O+∠BO′O=60°+60°=120°。 ∴的长度。 ③如图3所示,连接OA,OB, ∵OA=OB=AB=2, ∴△AOB为等边三角形。 过点O作OE⊥AB于点E,∴OE=OA•sin60°=。 ∴圆心O到弦AB的距离为。 (2)①如图4,当折叠后的与所在圆外切于点P时, 过点O作EF⊥AB交AB于点H、交于点E,交CD于点G、交于点F,即点E、H、P、O、G、F在直径EF上。 ∵AB∥CD,∴EF垂直平分AB和CD。 根据垂径定理及折叠,可知PH=PE,PG=PF。 又∵EF=4,∴点O到AB.CD的距离之和d为: d=PH+PG=PE+PF=(PE+PF)=2。 ②如图5,当AB与CD不平行时,四边形是OMPN平行四边形。证明如下: 设O′,O″为和所在圆的圆心, ∵点O′与点O关于AB对称,点O″于点O关于CD对称, ∴点M为的OO′中点,点N为OO″的中点。 ∵折叠后的与所在圆外切, ∴连心线O′O″必过切点P。 ∵折叠后的与所在圆与⊙O是等圆, ∴O′P=O″P=2,∴PM=OO″=ON,PN=OO′=OM, ∴四边形OMPN是平行四边形。 【考点】翻折变换(折叠问题)相切两圆的性质,等边三角形的判定和性质,平行四边形的判定,垂径定理,弧长的计算,解直角三角形,三角形中位线定理。 【分析】(1)①折叠后的所在圆O′与⊙O是等圆,可得O′A的长度。 ②如图2,过点O作OE⊥AB交⊙O于点E,连接OA.OB.AE、BE,可得△OAE、△OBE为等边三角形,从而得到的圆心角,再根据弧长公式计算即可。 ③如图3,连接OA.OB,过点O作OE⊥AB于点E,可得△AOB为等边三角形,根据三角函数的知识可求折叠后求圆心O到弦AB的距离。 (2)①如图4,与所在圆外切于点P时,过点O作EF⊥AB交于点E,交于点F,根据垂径定理及折叠,可求点O到AB.CD的距离之和。 ②由三角形中位线定理,根据两组对边分别相等的四边形是平行四边形即可得证。 287. (2012甘肃白银10分)如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,,延长DB到点F,使,连接AF. (1)证明:△BDE∽△FDA; (2)试判断直线AF与⊙O的位置关系,并给出证明. 【答案】解:(1)证明:在△BDE和△FDA中,∵FB=BD,AE=ED,∴。 又∵∠BDE=∠FDA,∴△BDE∽△FDA。 (2)直线AF与⊙O相切。证明如下: 连接OA,OB,OC, ∵AB=AC,BO=CO,OA=OA, ∴△OAB≌△OAC(SSS)。∴∠OAB=∠OAC。 ∴AO是等腰三角形ABC顶角∠BAC的平分线。 ∴AO⊥BC。 ∵△BDE∽FDA,得∠EBD=∠AFD,∴BE∥FA。 ∵AO⊥BE,∴AO⊥FA。∴直线AF与⊙O相切。 【考点】相似三角形的判定和性质,全等三角形的判定和性质,等腰三角形的性质,平行的判定和性质,切线的判定。 【分析】(1)因为∠BDE公共,夹此角的两边BD:DF=ED:AD=2:3,由相似三角形的判定,可知△BDE∽△FDA。 (2)连接OA、OB、OC,证明△OAB≌OAC,得出AO⊥BC.再由△BDE∽FDA,得出∠EBD=∠AFD,则BE∥FA,从而AO⊥FA,得出直线AF与⊙O相切。 288. (2012甘肃白银12分)已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处. (1)求点C的坐标; (2)若抛物线经过C、A两点,求此抛物线的解析式; (3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作y轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. 【答案】解:(1)过C作CH⊥OA于H, ∵在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,∴OA=。 ∵将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处, ∴OC=OA=,∠AOC=60°。 ∴OH=,CH=3 。 ∴C的坐标是(,3)。 (2)∵抛物线经过C(,3)、A(,0)两点, ∴,解得。∴此抛物线的解析式为 (3)存在。 ∵的顶点坐标为(,3),即为点C。 MP⊥x轴,设垂足为N,PN=t, ∵∠BOA=300,所以ON= ∴P() 作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E。 把代入得:。 ∴ M(,),E(,)。 同理:Q(,t),D(,1)。 要使四边形CDPM为等腰梯形,只需CE=QD, 即,解得:,(舍去)。 ∴ P点坐标为(,)。 ∴ 存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐为(,)。 【考点】二次函数综合题,翻折变换(折叠问题),折叠对称的,解二元一次方程和一元二次方程,曲线上点的坐标与方程的关系,含30度角的直角三角形的性质,勾股定理,等腰梯形的判定。 【分析】(1)过C作CH⊥OA于H,根据折叠得到OC=OA=4,∠A0C=60°,求出OH和CH即可。 (2)把C(,3)、A(,0)代入得到方程组,求出方程组的解即可。 (3)如图,根据等腰梯形的判定,只要CE=QD即可,据此列式求解。 289. (2012吉林长春10分)如图,在平面直角坐标系中,直线y=-2x+42交x轴与点A,交直线y=x于点B,抛物线分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4,点P在这条抛物线上. (1)求点C、D的纵坐标. (2)求a、c的值. (3)若Q为线段OB上一点,且P、Q两点的纵坐标都为5,求线段PQ的长. (4)若Q为线段OB或线段AB上的一点,PQ⊥x轴,设P、Q两点之间的距离为d(d>0),点Q的横坐标为m,直接写出d随m的增大而减小时m的取值范围. (参考公式:二次函数图像的顶点坐标为) 【答案】解:(1)∵点C在直线AB:y=-2x+42上,且C点的横坐标为16, ∴y=-2×16+42=10,即点C的纵坐标为10。 ∵D点在直线OB:y=x上,且D点的横坐标为4,∴点D的纵坐标为4。 (2)由(1)知点C的坐标为(16,10),点D的坐标为(4,4), ∵抛物线经过C、D两点, ∴,解得:。∴抛物线的解析式为。 (3)∵P为线段OB上一点,纵坐标为5,∴P点的横坐标也为5。 ∵点Q在抛物线上,纵坐标为5,∴,解得。 当点Q的坐标为(,5),点P的坐标为(5,5),线段PQ的长为; 当点Q的坐标为( ,5),点P的坐标为(5,5),线段PQ的长为。 所以线段PQ的长为或。 (4)当0≤m<4或12≤m<16时,d随m的增大而减小。 【考点】二次函数综合题,曲线上点的坐标与方程的关系,解二元一次方程组和一元二次方程,二次函数的性质。 【分析】(1)点C在直线AB:y=-2x+42上,将C点的横坐标,代入即可求出C点的纵坐标,同理可知:D点在直线OB:y=x上,将D点的横坐标,代入解析式即可求出D点的纵坐标。 (2)抛物线经过C、D两点,列出关于a和c二元二次方程组,解出a和c即可。 (3)根据Q为线段OB上一点,P、Q两点的纵坐标都为5,则可以求出Q点的坐标,又知P点在抛物线上,求出P点的坐标即可,P、Q两点的横坐标的差的绝对值即为线段PQ的长。 (4)根据PQ⊥x轴,可知P和Q两点的横坐标相同,求出抛物线的顶点坐标和B点的坐标,①当Q是线段OB上的一点时,结合图形写出m的范围,②当Q是线段AB上的一点时,结合图形写出m的范围即可: 根据题干条件:PQ⊥x轴,可知P、Q两点的横坐标相同, ∵抛物线y=,∴顶点坐标为(8,2)。 联立,解得点B的坐标为(14,14)。 ①当点Q为线段OB上时,如图所示,当0≤m<4或 12≤m≤14时,d随m的增大而减小; ②当点Q为线段AB上时,如图所示,当14≤m<16时,d 随m的增大而减小。 综上所述,当0≤m<4或12≤m<16时,d随m的增大而减小。 290. (2012吉林长春10分)如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,D、E分别为边AB、BC的中点,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作 PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s). (1)当点P在线段DE上运动时,线段DP的长为______cm,(用含t的代数式表示). (2)当点N落在AB边上时,求t的值. (3)当正方形PQMN与△ABC重叠部分图形为五边形时,设五边形的面积为S(cm²),求S与t的函数关系式. (4)连结CD.当点N于点D重合时,有一点H从点M出发,在线段MN上以2.5cm/s的速度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB上运动时,点H始终在线段MN的中心处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围. 【答案】解:(1)t-2。 (2)当点N落在AB边上时,有两种情况: ①如图(2)a,当点N与点D重合时,此时点P在DE上,DP=2=EC,即t-2=2,t=4。 ②如图(2)b,此时点P位于线段EB上. ∵DE=1 2 AC=4,∴点P在DE段的运动时间为4s, ∴PE=t-6,∴PB=BE-PE=8-t,PC=PE+CE=t-4。 ∵PN∥AC,∴△BNP∽△BAC。∴PN:AC = PB:BC=2,∴PN=2PB=16-2t。 由PN=PC,得16-2t=t-4,解得t=。 综上所述,当点N落在AB边上时,t=4或t=。 (3)当正方形PQMN与△ABC重叠部分图形为五边形时,有两种情况: ①当2<t<4时,如图(3)a所示。 DP=t-2,PQ=2,∴CQ=PE=DE-DP=4-(t-2)=6-t,AQ=AC-CQ=2+t,AM=AQ-MQ=t。 ∵MN∥BC,∴△AFM∽△ABC。∴FM:BC = AM:AC=1:2,即FM:AM=BC:AC=1:2。 ∴FM=AM=t. ∴ 。 ②当<t<8时,如图(3)b所示。 PE=t-6,∴PC=CM=PE+CE=t-4,AM=AC-CM=12-t,PB=BE-PE=8-t, ∴FM=AM=6-t,PG=2PB=16-2t, ∴ 。 综上所述,S与t的关系式为:。 (4)在点P的整个运动过程中,点H落在线段CD上时t的取值范围是:t=或t=5或 6≤t≤8。 【考点】动点问题上,相似形综合题,勾股定理,相似三角形的判定和性质,梯形和三角形的面积。 【分析】(1)∵在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,∴由勾股定理得AB=cm。 ∵D为边AB的中点,∴AD=cm。 又∵点P在AD上以cm/s的速度运动,∴点P在AD上运动的时间为2s。 ∴当点P在线段DE上运动时,在线段DP上的运动的时间为t-2s。 又∵点P在DE上以1cm/s的速度运动,∴线段DP的长为t-2 cm。 (2)当点N落在AB边上时,有两种情况,如图(2)所示,利用运动线段之间的数量关系求出时间t的值。 (3)当正方形PQMN与△ABC重叠部分图形为五边形时,有两种情况,如图(3)所示,分别用时间t表示各相关运动线段的长度,然后利用求出面积S的表达式。 (4)本问涉及双点的运动,首先需要正确理解题意,然后弄清点H、点P的运动过程: 依题意,点H与点P的运动分为两个阶段,如下图所示: ①当4<t<6时,此时点P在线段DE上运动,如图(4)a所示。 此阶段点P运动时间为2s,因此点H运动距离为2.5×2=5cm,而MN=2, 则此阶段中,点H将有两次机会落在线段CD上: 第一次:此时点H由M→H运动时间为(t-4)s,运动距离MH=2.5(t-4), ∴NH=2-MH=12-2.5t。 又DP=t-2,DN=DP-2=t-4, 由DN=2NH得到:t-4=2(12-2.5t),解得t=。 第二次:此时点H由N→H运动时间为t-4-=(t-4.8)s,运动距离NH=2.5(t-4.8)=2.5t-12, 又DP=t-2,DN=DP-2=t-4, 由DN=2NH得到:t-4=2(2.5t-12),解得t=5。 ②当6≤t≤8时,此时点P在线段EB上运动,如图(4)b所示。 由图可知,在此阶段,始终有MH=MC,即MN与CD的交点始终为线段MN的中点,即点H。 综上所述,在点P的整个运动过程中,点H落在线段CD上时t的取值范围是:t=或t=5或6≤t≤8。 291. (2012江西省10分)如图,已知二次函数L1:y=x2﹣4x+3与x轴交于A.B两点(点A在点B左边),与y轴交于点C. (1)写出二次函数L1的开口方向、对称轴和顶点坐标; (2)研究二次函数L2:y=kx2﹣4kx+3k(k≠0). ①写出二次函数L2与二次函数L1有关图象的两条相同的性质; ②是否存在实数k,使△ABP为等边三角形?如果存在,请求出k的值;如不存在,请说明理由; ③若直线y=8k与抛物线L2交于E、F两点,问线段EF的长度是否发生变化?如果不会,请求出EF的长度;如果会,请说明理由. 【答案】解:(1)∵抛物线, ∴二次函数L1的开口向上,对称轴是直线x=2,顶点坐标(2,﹣1)。 (2)①二次函数L2与L1有关图象的两条相同的性质: 对称轴为x=2;都经过A(1,0),B(3,0)两点。 ②存在实数k,使△ABP为等边三角形. ∵,∴顶点P(2,-k). ∵A(1,0),B(3,0),∴AB=2 要使△ABP为等边三角形,必满足|-k|=, ∴k=±。 ③线段EF的长度不会发生变化。 ∵直线y=8k与抛物线L2交于E、F两点, ∴kx2﹣4kx+3k=8k,∵k≠0,∴x2﹣4x+3=8。解得:x1=﹣1,x2=5。 ∴EF=x2﹣x1=6。∴线段EF的长度不会发生变化。 【考点】二次函数综合题,二次函数的性质,等边三角形的性质,解直角三角形。 【分析】(1)抛物线y=ax2+bx+c中:a的值决定了抛物线的开口方向,a>0时,抛物线的开口向上;a<0时,抛物线的开口向下。抛物线的对称轴方程和顶点坐标,可化为顶点式或用公式求解。 (2)①新函数是由原函数的各项系数同时乘以k所得,因此从二次函数的图象与解析式的系数的关系入手进行分析。 ②当△ABP为等边三角形时,P点必为函数的顶点,首先表示出P点纵坐标,它的绝对值正好是等边三角形边长的倍,由此确定k的值。 ③联立直线和抛物线L2的解析式,先求出点E、F的坐标,从而可表示出EF的长,若该长度为定值,则线段EF的长不会发生变化。 292. (2012江西省10分)已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作. (1)如图2,折叠后的所在圆的圆心为O′时,求的长度; (2)如图3,当弦AB=2时,求折叠后所在圆的圆心O’到弦AB的距离; (3)在图1中,再将纸片⊙O沿弦CD折叠操作. ①如图4,当AB∥CD,折叠后的与所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值; ②如图5,当AB与CD不平行,折叠后的与所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论. 【答案】解:(1)当经过圆O时,折叠后的所在圆O′在⊙O上,如图2所示,连接O′A.OA.O′B,OB,OO′。 ∵△OO′A,△OO′B为等边三角形, ∴∠AO′B=∠AO′O+∠BO′O=60°+60°=120°。 ∴的长度。 (2)如图3所示,连接O′A,O′B, ∵O′A=O′B=AB=2, ∴△AOB为等边三角形。 过点O作OE⊥AB于点E,∴O′E=O′A•sin60°=。 ∴折叠后所在圆的圆心O’到弦AB的距离为。 (3)①如图4,当折叠后的与所在圆外切于点P时, 过点O作EF⊥AB交AB于点H、交于点E,交CD于点G、交于点F,即点E、H、P、O、G、F在直径EF上。 ∵AB∥CD,∴EF垂直平分AB和CD。 根据垂径定理及折叠,可知PH=PE,PG=PF。 又∵EF=4,∴点O到AB.CD的距离之和d为: d=PH+PG=PE+PF=(PE+PF)=2。 ②如图5,当AB与CD不平行时,四边形是OMPN平行四边形。证明如下: 设O′,O″为和所在圆的圆心, ∵点O′与点O关于AB对称,点O″于点O关于CD对称, ∴点M为的OO′中点,点N为OO″的中点。 ∵折叠后的与所在圆外切, ∴连心线O′O″必过切点P。 ∵折叠后的与所在圆与⊙O是等圆, ∴O′P=O″P=2,∴PM=OO″=ON,PN=OO′=OM, ∴四边形OMPN是平行四边形。 【考点】翻折变换(折叠问题)相切两圆的性质,等边三角形的判定和性质,平行四边形的判定,垂径定理,弧长的计算,解直角三角形,三角形中位线定理。 【分析】(1)如图2,过点O作OE⊥AB交⊙O于点E,连接OA.OB.AE、BE,可得△OAE、△OBE为等边三角形,从而得到的圆心角,再根据弧长公式计算即可。 (2)如图3,连接O′A.O′B,过点O′作O′E⊥AB于点E,可得△AO′B为等边三角形,根据三角函数的知识可求折叠后求所在圆的圆心O′到弦AB的距离。 (3)①如图4,与所在圆外切于点P时,过点O作EF⊥AB交于点E,交于点F,根据垂径定理及折叠,可求点O到AB.CD的距离之和。 ②由三角形中位线定理,根据两组对边分别相等的四边形是平行四边形即可得证。 293. (2012甘肃兰州10分)若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=,x1•x2=.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|= 。 参考以上定理和结论,解答下列问题: 设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形. (1)当△ABC为直角三角形时,求b2-4ac的值; (2)当△ABC为等边三角形时,求b2-4ac的值. 【答案】解:(1)当△ABC为直角三角形时, 过C作CE⊥AB于E,则AB=2CE。 ∵抛物线与x轴有两个交点,△=b2-4ac>0, 则|b2-4ac|=b2-4ac。 ∵a>0,∴AB。 又∵CE,∴。 ∴,即。 ∵b2-4ac>0,∴b2-4ac=4。 (2)当△ABC为等边三角形时,由(1)可知CE=AB, ∴。 ∵b2-4ac>0,∴b2-4ac=12。 【考点】抛物线与x轴的交点,根与系数的关系,等腰三角形的性质,等边三角形的性质。 【分析】(1)当△ABC为直角三角形时,由于AC=BC,所以△ABC为等腰直角三角形,过C作CE⊥AB于E,则AB=2CE.根据本题定理和结论,得到AB,根据顶点坐标公式,得到CE,列出方程,解方程即可求出b2-4ac的值。 (2)当△ABC为等边三角形时,解直角△ACE,得CE=AB,据此列出方程,解方程即可求出b2-4ac的值。 294.(2012甘肃兰州12分)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线x=上. (1)求抛物线对应的函数关系式; (2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD 是菱形时,试判断点C和点D是否在该抛物线上,并说明理由; (3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标; (4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由. 【答案】解:(1)∵抛物线y=x2+bx+c经过点B(0,4),∴c=4。 ∵顶点在直线x=上,∴,解得。 ∴所求函数关系式为。 (2)在Rt△ABO中,OA=3,OB=4,∴。 ∵四边形ABCD是菱形,∴BC=CD=DA=AB=5。 ∴C、D两点的坐标分别是(5,4)、(2,0), 当x=5时,; 当x=2时,。 ∴点C和点D都在所求抛物线上。 (3)设CD与对称轴交于点P,则P为所求的点, 设直线CD对应的函数关系式为y=kx+b, 则,解得,。∴直线CD对应的函数关系式为。 当x=时,。∴P()。 (4)∵MN∥BD,∴△OMN∽△OBD。 ∴,即,得。 设对称轴交x于点F,则。 ∵, , (0<t<4)。 ∵,,0<<4, ∴当时,S取最大值是。此时,点M的坐标为(0,)。 【考点】二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,二次函数的性质,菱形的性质,相似三角形的判定和性质。 【分析】(1)根据抛物线y=x2+bx+c经过点B(0,4),以及顶点在直线x=上,得出b,c即可。 (2)根据菱形的性质得出C、D两点的坐标分别是(5,4)、(2,0),利用图象上点的性质得出x=5或2时,y的值即可。 (3)首先设直线CD对应的函数关系式为y=kx+b,求出解析式,当x=时,求出y即可。 (4)利用MN∥BD,得出△OMN∽△OBD,进而得出,得到,从而表示出△PMN的面积,利用二次函数最值求出即可。 295. (2012吉林省10分)如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2. (1)当t= s时,点P与点Q重合; (2)当t= s时,点D在QF上; (3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式. 【答案】解:(1)1。 (2)。 (3)当P、Q重合时,由(1)知,此时t=1; 当D点在BC上时,如答图2所示,此时AP=BQ =t,BP=t, 又∵BP=2-t,∴t=2-t,解得t=。 进一步分析可知此时点E与点F重合。 当点P到达B点时,此时t=2。 因此当P点在Q,B两点之间(不包括Q,B两点)时,其运动过程可分析如下: ①当1<t≤时,如答图3所示,此时重合部分为梯形PDGQ。 此时AP=BQ=t,∴AQ=2-t,PQ=AP-AQ=2t-2。 易知△ABC∽△AQF,可得AF=2AQ,EF=2EG。 ∴EF=AF-AE=2(2-t)-t=4-3t,EG=EF=2-t。 ∴DG=DE-EG=t-(2-t)=t-2。 。 ②当<t<2时,如答图4所示,此时重合部分为一个多边形。 此时AP=BQ=t,∴AQ=PB=2-t。 易知△ABC∽△AQF∽△PBM∽△DNM, 可得AF=2AQ,PM=2PB,DM=2DN。∴AF=4-2t,PM=4-2t。 又DM=DP-PM=t-(4-2t)=3t-4,∴DN=(3t-4)。 综上所述,当点P在Q,B两点之间(不包括Q,B两点)时,S与t之间的函数关系式为:。 【考点】动点问题,正方形的性质,勾股定理,相似三角形的判定和性质。 【分析】(1)当点P与点Q重合时,此时AP=BQ=t,且AP+BQ=AB=2,由此得t+t=2,解得t=1(s)。 (2)当点D在QF上时,如答图1所示,此时AP=BQ=t. ∵QF∥BC,APDE为正方形,∴△PQD∽△ABC。 ∴DP:PQ=AC:AB=2,则PQ=DP=AP=t。 由AP+PQ+BQ=AB=2,得t+t+t=2,解得:t=。 (3)当点P在Q,B两点之间(不包括Q,B两点)时,运动过程可以划分为两个阶段: ①当1<t≤ 时,如答图3所示,此时重合部分为梯形PDGQ.先计算梯形各边长,然后利用梯形面积公式求出S。 ②当<t<2时,如答图4所示,此时重合部分为一个多边形.面积S由关系式“ ”求出。 296. (2012吉林省10分)问题情境 如图,在x轴上有两点A(m,0),B(n,0)(n>m>0).分别过点A,点B作x轴的垂线,交抛物线y=x2于点C、点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E、点F的纵坐标分别记为yE,yF. 特例探究 填空: 当m=1,n=2时,yE= ,yF= ; 当m=3,n=5时,yE= ,yF= . 归纳证明 对任意m,n(n>m>0),猜想yE与yF的大小关系,并证明你的猜想. 拓展应用 (1)若将“抛物线y=x2”改为“抛物线y=ax2(a>0)”,其他条件不变,请直接写出yE与yF的大小关系; (2)连接EF,AE.当时,直接写出m与n的关系及四边形OFEA的形状. 【答案】解:特例探究:2,2;15,15。 归纳证明:。证明如下: 对任意m,n(n>m>0)时,,,所以直线OC的解析式为:;直线OD的解析式为:;此时 解得,,∴;解得,,∴。 ∴此时。 拓展应用:(1)。 (2)n=2m;四边形OFEA是平行四边形。 【考点】一次函数、二次函数综合运用,函数图象上的点与函数解析式的关系,平行四边形的判定。 【分析】特例探究: 当m=1,n=2时,C(1,1),D(2,4),所以直线OC的解析式为:;直线OD的解析式为:;此时, 解得,E(2,2),∴yE=2;.解得,F(1,2),∴yF=2。 ∴此时。 当m=3,n=5时,C(3,9),D(5,25),所以直线OC的解析式为:;直线OD的解析式为:;此时, 解得,E(5,15),∴yE=15;解得,F(3,15),∴yF=15。. ∴此时。 归纳证明:与特例探究的求法类同。 拓展应用:(1)若将“抛物线y=x2”改为“抛物线y=ax2(a>0)”,其他条件不变,仍然有:。 此时,,,所以直线OC的解析式为:;直线OD的解析式为:;此时 解得,,∴;解得,,∴。 ∴此时。 (2)由得 化简,得n=2m。 由n=2m得OB=2OA,∴EF=AB=OA。 又∵且EB⊥x轴,FA x轴,∴EF∥AB。 ∴四边形OFEA是平行四边形。 297. (2012青海西宁10分)2012年6月9日召开的青海省居民阶梯电价听证会,征求了消费者、经营者 和有关方面的意见,对青海省居民阶梯电价发、方案的必要性、可行性进行了论证.阶梯电价方案规定: 若每月用电量为130度以下,收费标准为0.38元/度;若每月用电量为131度~230度,收费标准由两部 分组成:①其中130度,按0.38元/度收费,②超出130度的部分按0.42元/度收费.现提供一居民某月电 费发票的部分信息如下表所示: 青海省居民电费专用发票 计费期限:一个月 用电量(度) 单价(元/度) 阶梯一:130 0.38 阶梯二:131~230(超出部分) 0.42 本月实付金额:78.8(元) (大写)柒拾捌元捌角 第 二 联 根据以上提供的信息解答下列问题: (1)如果月用电量用x(度)来表示,实付金额用y(元)来表示,请你写出这两种情况实付金额y与月用电 量x之间的函数关系式; (2)请你根据表中本月实付金额计算这个家庭本月的实际用电量; (3)若小芳和小华家一个月的实际用电量分别为80度和150度,则实付金额分别为多少元? 【答案】解:(1)根据题意得: 当x≤130时,y=0.38x; 当130<x≤230时,y=0.42(x-130)+0.38×130=0.42x-5.2; (2)∵0.38×130=49.4<78.8,∴当y=78.8时,用电量超出130度。 ∴0.42x-5.2=78.8,解得:x=200。 答:这个家庭一个月的实际用电量是200度。 (3)∵80度低于130度,∴收费标准为0.38元/度。∴80×0.38=30.4元。 ∵150度高于130度,∴超出的收费标准为0.42元/度。 ∴130×0.38+(150-130)×0.42=57.8元。 答:小芳和小华一个月的实付金额分别为30.4元和57.8元。 【考点】一次函数的应用。 【分析】(1)分用电量小于130度时,成正比例函数关系,实付金额等于单价乘以用电度数,131~230度时,成一次函数关系,实付金额等于130度内的用电付出金额与超出130度的用电付出金额的和,然后即可得到y与x的函数关系式。 (2)先计算出78.8元的用电量超出130度,然后把实付金额代入函数关系式进行计算即可得解。 (3)根据用电度数判断出适合的函数关系式,然后把用电度数代入关系式进行计算即可得解。 298. (2012青海西宁12分)如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,O在 x轴的正半轴上,已知A(0,4)、C(5,0).作∠AOC的平分线交AB于点D,连接CD,过点D作DE⊥CD 交OA于点E. (1)求点D的坐标; (2)求证:△ADE≌△BCD; (3)抛物线y=x2-x+4经过点A、C,连接AC.探索:若点P是x轴下方抛物线上一动点,过 点P作平行于y轴的直线交AC于点M.是否存在点P,使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由. 【答案】解:(1)∵OD平分∠AOC,∴∠AOD=∠DOC。 ∵四边形AOCB是矩形,∴AB∥OC。∴∠AOD=∠DOC。∴∠AOD=∠ADO。 ∴OA=AD(等角对等边)。 ∵A点的坐标为(0,4),∴D点的坐标为(4,4)。 (2)证明:∵四边形AOCB是矩形,∴∠OAB=∠B=90°,BC=OA。 ∵OA=AD,∴AD=BC。 ∵ED⊥DC,∴∠EDC=90°。∴∠ADE+∠BDC=90°。∴∠BDC+∠BCD=90°。 ∴∠ADE=∠BCD。 在△ADE和△BCD中,∵∠DAE=∠B,AD=BC,∠ADE=∠BCD, ∴△ADE≌△BCD(ASA)。 (3)存在。 ∵二次函数的解析式为:y=x2-x+4,点P是抛物线上的一动点,∴设P点坐标为(t,t 2-t+4 )。 设AC所在的直线的函数关系式为y=kx+b, ∵A(0,4)、C(5,0),∴,解得。 ∴直线AC的解析式为y=x+4。 ∵PM∥y轴,∴M(t,t+4)。 ∴PM=。 ∴当t=时,PM有最大值为5。 ∴所求的P点坐标为(,-3)。 【考点】二次函数综合题,矩形的性质,平行的性质,等腰三角形的判定,三角形内角和定理,全等三角形的判定和性质,待定系数法,曲线上点的坐标与方程的关系,二次函数的最值。 【分析】(1)根据OD平分∠AOC,可得∠AOD=∠DOC,再由AOBC是矩形,得到∠AOD=∠ADO,根据等角对等边可得到OA=AD,从而求出D点坐标。 (2)由四边形AOCB是矩形,得到∠OAB=∠B=90°,BC=OA,从而证明出AD=BC,再根据角之间的等量关系∠ADE=∠BCD,于是可证明出△ADE≌△BCD。 (3)设P点坐标为(t,t 2-t+4 ),设AC所在的直线的函数关系式为y=kx+b,根据A(0,4)、C(5,0),求出AC的解析式,进而用t表示出PM的长,利用二次函数的性质求出PM的最值,点P的坐标也可以求出。 299. (2012青海省10分)如图(*),四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题. (1)探究1:小强看到图(*)后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌EFC就行了,随即小强写出了如下的证明过程: 证明:如图1,取AB的中点M,连接EM. ∵∠AEF=90° ∴∠FEC+∠AEB=90° 又∵∠EAM+∠AEB=90° ∴∠EAM=∠FEC ∵点E,M分别为正方形的边BC和AB的中点 ∴AM=EC 又可知△BME是等腰直角三角形 ∴∠AME=135° 又∵CF是正方形外角的平分线 ∴∠ECF=135° ∴△AEM≌△EFC(ASA) ∴AE=EF (2)探究2:小强继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论. (3)探究3:小强进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程给小强看,若不成立请你说明理由. 【答案】解:(2)探究2,证明:在AB上截取AM=EC,连接ME, 由(1)知∠EAM=∠FEC。 ∵AM=EC,AB=BC,∴BM=BE。∴∠BME=45°。 ∴∠AME=∠ECF=135°。 ∵∠AEF=90°,∴∠FEC+∠AEB=90°。 又∵∠EAM+∠AEB=90°,∴∠EAM=∠FEC。 在△AEM和△EFC中,∵∠AME=∠ECF,∠AME=∠ECF,∠EAM=∠FEC, ∴△AEM≌△EFC(ASA)。∴AE=EF。 (3)探究3:成立。证明如下: 延长BA到M,使AM=CE,连接ME, ∴BM=BE。∴∠BME=45°。∴∠BME=∠ECF。 又∵AD∥BE,∴∠DAE=∠BEA。 又∵∠MAD=∠AEF=90°, ∴∠DAE+∠MAD=∠BEA+∠AEF, 即∠MAE=∠CEF。 在△MAE和△CEF中,∵∠BME=∠ECF,AM=CE,∠MAE=∠CEF, ∴△MAE≌△CEF(ASA)。∴AE=EF。 【考点】正方形的性质,平行的性质,全等三角形的判定和性质。 【分析】(2)在AB上截取AM=EC,然后证明∠EAM=FEC,∠AME=∠ECF=135°,再利用“ASA”证明△AEM和△EFC全等,然后根据全等三角形对应边相等即可证明。 (3)延长BA到M,使AM=CE,然后证明∠BME=45°,从而得到∠BME=∠ECF,再利用两直线平行,内错角相等证明∠DAE=∠BEA,然后得到∠MAE=∠CEF,再利用“ASA”证明△MAE和△CEF全等,根据全等三角形对应边相等即可得证。 300. (2012青海省12分)如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点. (1)求这个二次函数的表达式. (2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由. (3)当点P运动到什么位置时,四边形ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积. 【答案】解:(1)将B、C两点的坐标代入y=x2+bx+c得,解得。 ∴二次函数的表达式为:y=x2﹣2x﹣3。 (2)存在点P,使四边形POP′C为菱形。 设P点坐标为(x,x2﹣2x﹣3),PP′交CO于E, 若四边形POP′C是菱形,则有PC=PO。 连接PP′,则PE⊥CO于E。 ∴OE=EC=。 ∴x2﹣2x﹣3=, 解得(不合题意,舍去)。 ∴P点的坐标为()。 (3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2﹣2x﹣3), 设直线BC的解析式为y=kx+b,则 ,解得。∴直线BC的解析式为y=x﹣3。 则Q点的坐标为(x,x﹣3)。 ∴ ∴当时,四边形ABPC的面积最大,此时P点的坐标为,四边形ABPC的面积的最大值为。 【考点】二次函数综合题,曲线上点的坐标与方程的关系,翻折的性质,菱形的判定和性质,二次函数最值。190187 【分析】(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值。 (2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标。 (3)由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标。查看更多