- 2021-04-29 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上数学课件《全等三角形》 (17)_苏科版
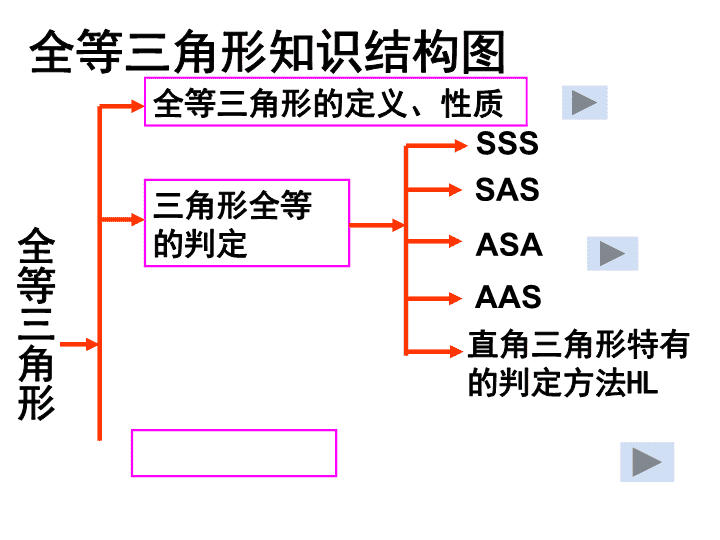
学习目标: (1)回顾全等三角形的概念、性质、判定方法,利 用全等三角形的性质和判定进行计算和证明。 (2)让学生经历观察、猜想、证明、归纳的过程, 发展学生合情合理的推理能力,渗透转化的数学思想。 (3)引导学生共同参与,激发数学求知欲,并养成 良好的数学学习惯。 学习重难点: 重点:利用全等三角形的性质和判定进行计算和证明。 难点:全等三角形的构造与证明。 全 等 三 角 形 三角形全等 的判定 全等三角形知识结构图 SSS SAS ASA AAS 全等三角形的定义、性质 直角三角形特有 的判定方法HL 一.全等三角形: 什么是全等三角形?一个三角形经过哪些变化 可以得到它的全等形? 全等三角形有哪些性质? 能够完全重合的两个三角形叫做全等三角形。 一个三角形经过平移、翻折、旋转可以得到 它的全等形。 (1):全等三角形的对应边相等、对应角相等。 (2):全等三角形的周长相等、面积相等。 (3):全等三角形的对应边上的对应中线、角平分线、 高线分别相等。 全等三角形的判定方法 一般三角形 全等的条件: 1.SSS; 2.SAS; 3.ASA; 4.AAS. 直角三角形 全等特有的条件:HL. 包括直角三角形 不包括其它形 状的三角形 解题 中常 用的 4种 方法 回顾知识点: 边边边:三边对应相等的两个三角形全等(可简写成 “SSS”) 边角边:两边和它们的夹角对应相等两个三角形全等(可 简写成“SAS”) 角边角:两角和它们的夹边对应相等的两个三角形全等 (可简写成“ASA”) 角角边:两角和其中一角的对边对应相等的两个三角形全 等(可简写成“AAS”) 斜边.直角边:斜边和一条直角边对应相等的两个直角三 角形全等(可简写成“HL”) AC=DF 方法指引 证明两个三角形全等的基本思路: (1):已知两边---- 找第三边 (SSS) 找夹角 (SAS) (2):已知一边一角--- 已知一边和它的邻角 找是否有直角 (HL) 已知一边和它的对角 找这边的另一个邻角(ASA) 找这个角的另一个边(SAS) 找这边的对角 (AAS) 找一角(AAS) 已知角是直角,找一边(HL) (3):已知两角--- 找两角的夹边(ASA) 找夹边外的任意边(AAS) 练习 如图,△ABC≌ △DEF,DE=4,AE=1,则BE 的长是( ) A.5 B.4 C.3 D.2 FE D CB A 我 能 行 C 7 我 能 行 AC=AE∠C=∠E∠B=∠D 如图,在△ABC和△BAD中,BC = AD,请 你再补充一个条件,使△ABC≌ △BAD.你 补充的条件是 . D A B C 1 我 能 行 AC=BD∠ABC=∠BAD (答案不唯一) 如图,某同学把一块三角形的玻璃打碎成了 三块,现在要到玻璃店去配一块完全一样的 玻璃,那么最省事的办法是拿( )去配. 我 能 行 ③ 我 能 行 如图,给出下列四组条件 ①AB=DE,BC=EF,AC=DF; ②AB=DE,∠B=∠E,BC=EF; ③∠B=∠E,BC=EF,∠C=∠F; ④AB=DE,AC=DF,∠B=∠E 其中能使△ABC≌△DEF的 是 .①②③ 如图,已知E在AB上,∠1=∠2, ∠3=∠4, 那么AC等于AD吗?为什么? 4 3 2 1E D C BA 解:AC=AD 理由:在△EBC和△EBD中 ∠1=∠2 ∠3=∠4 EB=EB ∴ △EBC≌ △EBD (AAS) ∴ BC=BD 在△ABC和△ABD中 AB=AB ∠1=∠2 BC=BD ∴ △ABC≌ △ABD (SAS) ∴ AC=AD 如图已知△ABC,AD是BC边上的中线, 分别以AB边、AC边为直角边各向外作等 腰直角三角形.求证:EF=2AD G 证明:延长AD到G,使DG=AD,连接BG ∵AD是BC边上的中线,∴BD=CD 在△ACD和△GBD中, ∴△ACD≌ △GBD(SAS) ∴AC=BG,∠CAD=∠G ∴AC∥BG,∴∠BAC+∠ABG=180° ∵△ABE与△ACF为等腰直角三角形 ∴AB=AE,AC=AF,∠BAE=∠CAF=90° ∴∠EAF+∠BAC=180° ∴∠ABG=∠EAF 在△ABG和△EAF中, ∴△ABG≌ △EAF(SAS) BDCD GDBADC GDAD AFBG EAFABG AEAB ∴AG=EF ∵AG=2AD ∴EF=2AD 要证明两条线段的和与一条线 段相等时常用的两种方法: 1、可在长线段上截取与两条 线段中一条相等的一段,然后 证明剩余的线段与另一条线段 相等。(截长) 2、把一个三角形移到另一位 置,使两线段补成一条线段, 再证明它与长线段相等。(补 短) 规律方法总结 在△ABC中, ∠ACB=90°,AC=BC,直线MN经过 点C, AD⊥MN于点D, BE ⊥MN于点E, (1)当直线MN旋转到图(1)的位置时,猜想线段 AD,BE,DE的数量关系,并证明你的猜想 N M E D C BA 图(1) 在△ABC中, ∠ACB=90°,AC=BC,直线MN经过 点C, AD⊥MN于点D, BE ⊥MN于点E, (2)当直线MN旋转到图(2)的位置时,猜想线段 AD,BE,DE的数量关系,并证明你的猜想N M E D C BA 图(2) 本节课你有哪些收获?查看更多