八年级上数学课件- 13-3-1 等腰三角形 课件（共23张PPT）_人教新课标

八年级上数学课件- 13-3-1 等腰三角形 课件（共23张PPT）_人教新课标

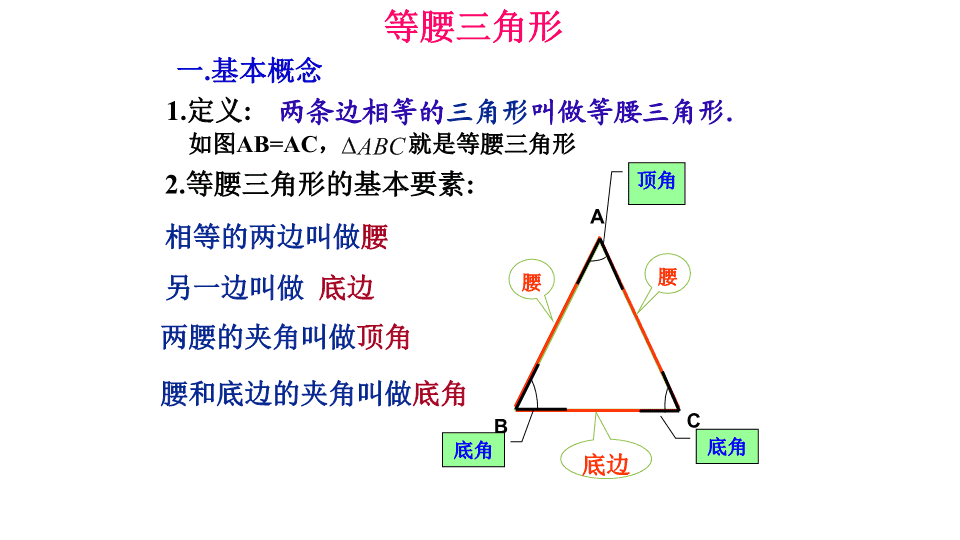
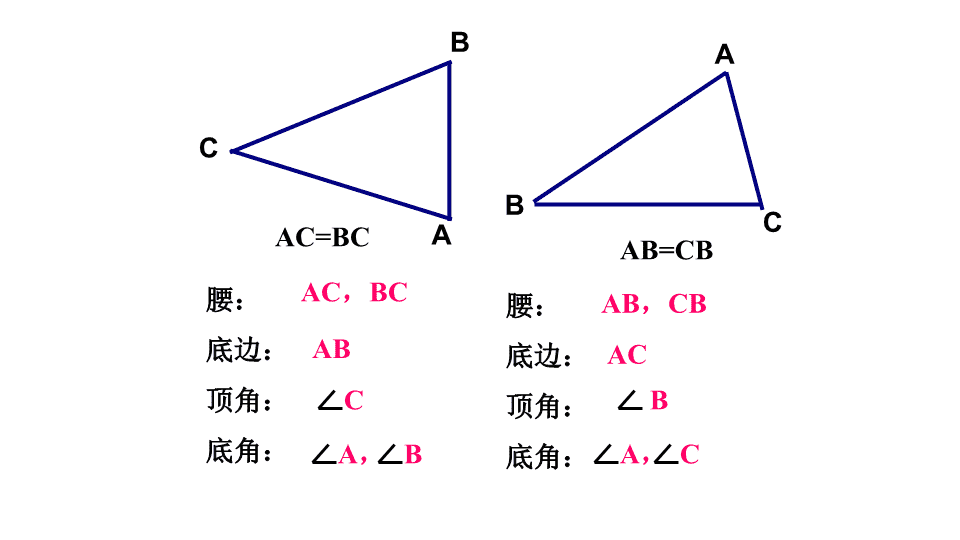
等腰三角形 等腰三角形 一.基本概念 1.定义: 两条边相等的三角形叫做等腰三角形. 如图AB=AC， 就是等腰三角形 ABC 2.等腰三角形的基本要素: 相等的两边叫做腰 另一边叫做 底边 两腰的夹角叫做顶角 腰和底边的夹角叫做底角 A B C 腰腰 底边 顶角 底角 底角 C A B AC=BC B C A AB=CB 腰： 底边： 顶角： 底角： 腰： 底边： 顶角： 底角： AC，BC AB A， B AB，CB AC B A， C C 做一做1： （3）把等腰三角形对折，让两腰AB，AC重叠在 一起，折痕为AD。 观察后你发现了什么现象？ 二.等腰三角形性质的探索 B A CD A B CD 1、等腰三角形是轴对称图形 2、∠ B =∠ C 3、BD = CD ，AD 为底边上的中线 ∠ADB = ∠ADC = 90°，AD为底边上的高 ∠BAD = ∠CAD ，AD为顶角平分线 C A B D 做一做2：画出手中等腰三角形的某一底 角平分线、对边(腰)上的中线和高，看 是否重合？ 等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合，简称“三线合一” 判断正误 等腰三角形的角平分线、中线和高互相重合。 G E CB A F 如图：BF为AC边上的高，BE为 ABC的平分线， BG为AC边上的中线 C A B D 等腰三角形的性质 1、等腰三角形的两个底角相等 （简称“等边对等角”） 2、等腰三角形的 顶角平分线、底边上的高和底边上的中线 互相重合（简称“三线合一”） 一般的三角 形有这种性 质吗？ 要注意是指顶角 的平分线、底边 上的高、底边上 的中线这三线重 合。 CDB A ①在ΔABC中，∵AB=AC， ∴ ∠B=∠C（ ） 等腰三角形的性质 等边对等角 （1）∵AD⊥BC， ∴∠____ = ∠____，___= ___ （2）∵AD是中线， ∴___⊥___ ，∠____ =∠____ （3）∵AD是角平分线， ∴___ ⊥___ ，___ =___ BAD CAD BD CD AD BC AD BC BAD CAD BD CD ②在△ABC中， AB=AC时， 等腰三角形底边上 的中线和高线、顶 角的平分线互相重 合。 例1、如图，在△ABC中，AB = AC，D是BC边上的中点， ∠B = 30°，求 ∠1 和 ∠ADC的度数。 A B C 1 2 D 解： 因为AD是底边上的中线 根据等腰三角形的“三线合一” 所以AD是△ABC的顶角平分线、 底边上的高，即 ∠1 = ∠ 2 ∠ADC = 90° 因为 ∠ BAC =180° - 30°-30° = 120° 所以 060 2 1    BAC 1.等腰三角形一个角为70°,它的另外两个角为 ___________________ 2.等腰三角形一个角为110°,它的另外两个角为 ________ 70°,40°或55°,55° 35°,35° 巩固练习: 3等腰三角形有两边长为6和8，则该等腰三角形的周长为 4.等腰三角形有两边长为4和8，则该等腰三角形的 周长为 20或22 20 2、如图，在△ABC中，已知 AB = AC ，AD为∠BAC 的平分线，且∠2=25°，求∠ADB和∠B的度数。 D 1 2 A B C 1、等腰三角形的性质： 等边对等角 2、等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合（三线合一） 3、“三线合一”性质在实际应用中，只要推出 其中一个 结论成立，其它两个结论一下成立， 所以关键是寻找其中一个结论成立的条件。 1、等腰三角形的周长为16，其中一条边的长是6， 求另两边的长。 2、等腰三角形的底角比顶角大15 °，求各内角的 度数. 4、等腰三角形的底角可以是直角或钝角吗？为什么？ 补充例题： 的度数；时，求）当（ 边上的高。是 ，中，如图，在 BCDA ABCD ACABABC   401 D A B C 的度数；时，求）当（ BCDA  1402 的度数；时，求）当（ BCDA  3 达标练习二(A 水平) 一、填空题： 1、等腰三角形若两边长为3和7，则其周长为________。 2、如果等腰三角形的一个底角为50°，那么其余两个角为______和 ______。 3、如果等腰三角形的顶角为80°，那么它的一个底角为________。 二、判断题： 1、等腰三角形的底角都是锐角( ) 2、钝角三角形不可能是等腰三角形( ) √ × 17　　 50° 80° 50° 达标练习二(B水平) 1、若等腰三角形的一个内角为 40°,则它的另外两 个内角为__________________ 2、 若等腰三角形的一个内角为120°,则它的另外两 个内角为______ 70°,70°或40°，100 ° 30°,30° ① 顶角+2×底角=180° ② 顶角=180°－2×底角 ③ 底角=（180°－顶角）÷2 结论:在等腰三角形中，已知一个角，就可以求出另外两个角。 ④当已知任意一个内角时,则要分情况讨论 3、如图，在Rt△ABC中，∠ACB=900， ∠CAB 的平分线AD交BC于D，AB边上的高线CE交AB于 E，交AD于F，求证：CD=CF B AC ED 1 2 3 F 分析： CD=CF ∠1=∠2 ∠1=∠B+∠BAD ∠2=∠3+∠DAC ∠3=∠B ∠ACB =90°，CE是AC边上高 挑战：已知等腰三角形一腰上的中线将三角形周长分 成２：１两部分，已知三角形底边长为５，求腰长？ 解：如图，令CD＝x，则AD＝x，AB＝2x ∵底边BC＝5 ∴BC＋CD＝5＋x AB＋AD＝3x ∴(5+x)：3x＝2:1 　或3x：(5+x)=2:1 Ａ Ｂ Ｃ Ｄ x x 2x 5 例4.如图，已知△ABC中，AB=AC，BD=BC，AD=DE=EB,求 ∠A的度数. 解：设∠A=x ，∠EBD=y，∠C=z ∵AB=AC ∴∠ABC=∠C=z ∵BD=BC ∴∠C=∠BDC=z ∵BE=DE ∴∠EBD=∠EDB=90° ∵AD=DE ∴∠A=∠AED=x 又∵∠BDC=∠A+∠ABD， ∠AED=∠EBD+∠EDB （三角形的外角等于和它不相邻的两个内角的和） ∠A+∠ABC+∠ACB=180°（三角形内角和为 180°） ∴解得x=45° 即：∠A=45°         180 2 zzx yxz yx A B C D E x y zx y z 挑战５：如图，已知CE、CF分别平分 ∠ACB和它的外角，EF∥BC，EF交AC 于D，你能说明DE＝DF的理由吗？ FDE A B C G 再 见！